СРРиТ / Расчетная работа по МСТК

Министерство образования Республики Беларусь

Учреждение образования

Белорусский государственный университет информатики и радиоэлектроники

Кафедра систем телекоммуникаций

Расчётная работа

по дисциплине

«Моделирование систем телекоммуникаций»

Минск, 2009

ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ

АМ – амплитудная модуляция;

АЧХ – аплитудно-частотная характеристика;

ПФ – полосовой фильтр;

ТВ – телевизионный;

ХРЗ – характеристика рабочего затухания;

ФНЧ – фильтр нижних частот;

ФЧХ – фазочастотная характеристика.

1. Цель работы: спроектировать линейные звенья системы передачи ТВ сигналов по методу рабочих параметров, исследовать частотные свойства этих звеньев посредствам моделирования их АЧХ, ФЧХ и ХРЗ.

2. Условие:

Рассматривается система передачи ТВ сигналов с двухполосной АМ (рис. 1):

Рисунок 1. − Структурная схема системы передачи ТВ сигналов

Идентификационные коэффициенты:

, − число букв в фамилии студента;

, − число букв в имени студента;

, − число букв в отчестве студента;

, , − коэффициенты, представляющие число

в -разрядной двоичной системе исчисления.

N_ф = 4, N_и =3, N_о = 0.

b₂ = 1, b₁ = 1, b₀ = 0.

Таблица 1 − Численные значения технических параметров

Параметры	Значения параметров
NФ	4
aD1, дБ	0.30
aS1, дБ	26
aD6, дБ	0.20
aS6, дБ	22
aD9, дБ	1.30
aS9, дБ	30
f0, МГЦ	90
t1Н	0
t2Н	1
t3Н	6
t4Н	6

где f₀ — несущая частота исследуемой системы передачи (рисунок 1);

F_D1, (F_D9) — граничная частота полосы пропускания ФНЧ 1 (9);

F_S1, (F_S9) — граничная частота полосы задерживания ФНЧ 1 (9);

F_+D6 (F_-D6) — верхняя (нижняя) граничная частота полосы пропускания ПФ 6;

F_+S6 (F_-S6) — верхняя (нижняя) граничная частота полосы задерживания ПФ 6;

а₁(f) (а₆(f), а₉(f)) — характеристика рабочего затухания ФНЧ 1 (ПФ 6, ФНЧ 9);

а_D1 (а_D6, а_D9) — допустимая неравномерность характеристики рабочего затухания ФНЧ 1 (ПФ 6, ФНЧ 9) в полосе пропускания;

а_S1 (а_S6, а_S9) — минимальное рабочее затухание ФНЧ 1 (ПФ 6, ФНЧ 9) в полосе .задерживания;

_k − круговая частота, характеризующая свойства измерительного сигнала;

− нормированные (к частоте _k) моменты времени.

F_D1=(1+0.1∙) F_D10 = (F_D10=3·10⁶ Гц);

F_S1=(1+0.1∙) F_S10 = (F_S10=6·10⁶ Гц);

F_D9=F_D90/(1+0.1∙) = (F_D90=6 10⁶ Гц);

F_S9=F_S90/(1+0.1∙) = (F_S90=12 10⁶ Гц);

F_+D6=f₀+(1+)F_D10 = ; F_-D6= f₀−(1+)F_D10 = ;

F_+S6= f₀+(1+)F_S10 = ; F_-S6= f₀−(1+)F_S10 = ;

= 0 с; = ;

= ; = ;

_k=3 10⁶ рад/с.

3. Расчётная часть

3.1. Процедура 1

а). Построим операторную передаточную функцию ФНЧ 1 (рисунок 1), используя метод рабочих параметров и выбирая ХРЗ модели Золотарева-Кауэра (идентификационный коэффициент =0):

Рисунок 2– Общий вид ХРЗ ФНЧ

ХРЗ реального ФНЧ имеет три области: I – полоса пропускания (0‑_D); II – переходная область (_D‑_S); III – полоса задерживания (_S‑). Здесь: _D (_S)– граничная частота полосы пропускания (задерживания); a_D – неравномерность ХРЗ в полосе пропускания; a_S – гарантированное затухание в полосе задерживания. Характеристика считается заданной, если известны все приведенные параметры.

a_D1 = 0.3 дБ; F_D1 =

a_S1 = 26 дБ; F_S1 =

Таким образом, из справочника [1] подберём фильтр-прототип:

• тип фильтра — С0325;

• с = 4.791901348;

• ;

• ;

• ;

• 

• 

• 

• 

• 

Заменим :

Построим нормированные АЧХ, ФЧХ и ХРЗ в среде Mathcad:

Рис. 3.1 – Нормированная АЧХ ФНЧ₁

Рис. 3.2 – АЧХ ФНЧ₁

Рис. 3.1 – Нормированная АЧХ ФНЧ₁

Рис. 4.1 – Нормированная ФЧХ ФНЧ₁

Рис. 4.2 – ФЧХ ФНЧ₁

Рис. 5.1 – Нормированная ХРЗ ФНЧ₁

Рис. 5.2 – ХРЗ ФНЧ₁

Денормирование характеристик производили следующим образом: , где — нормирующая частота (граничная частота полосы пропускания ФНЧ₁) — равная = 24.5.

б). Построим операторную передаточную функцию К₆(р) ПФ₆, используя метод рабочих параметров и выбирая ХРЗ модели Чебышева (b₁=1):

a_D6 = 0,2 дБ; a_S6 = 22 дБ;

F_+D6 = ; F_-D6= ;

F_+S6= ; F_-S6= .

.

Рисунок 6 - Общий вид ХРЗ ПФ

ХРЗ ПФ имеет пять областей: I (V) – нижняя (верхняя) полоса задерживания (0‑_-S) ((_+S ‑ )); II (IV) – нижняя (верхняя) переходная область (_-S ‑ _-D) ((_+D ‑ _+S)); III – полоса пропускания (_-D ‑ _+D). Здесь: _-S (_+S) – нижняя (верхняя) граничная частота полосы задерживания; _-D (_+D) – нижняя (верхняя) граничная частота полосы пропускания; a_D – неравномерность ХРЗ в полосе пропускания; a_S – гарантированное затухание в полосах задерживания. Характеристика считается заданной, если известны все приведенные параметры.

Зная численные значения основных параметров, теперь можем подобрать нужный фильтр-прототип для данного ПФ₆:

• тип фильтра – Т02еb;

• с = 0.516397779;

• ;

• 

• 

• 

• 

• 

Осуществим преобразование ФНЧ → ПФ, заменив :

, где .

Заменим :

Построим нормированные и реальные АЧХ, ФЧХ и ХРЗ в среде Mathcad:

Рис. 7.1 — Нормированная АЧХ ПФ₆

Рис. 7.2 —АЧХ ПФ₆

Рис. 8.1 – Нормированная ФЧХ ПФ₆

Рис. 8.2 –ФЧХ ПФ₆

Рис. 9.1 – Нормированная ХРЗ ПФ₆

Рис. 9.2 – ХРЗ ПФ₆

в). Построим операторную передаточную функцию К₉(р) ФНЧ₉, используя метод рабочих параметров и выбирая ХРЗ модели Чебышева (b₂=1):

a_D9 = 1,3 дБ; F_D9 =

a_S9 = 30 дБ; F_S9 =

Зная численные значения основных параметров, теперь можем подобрать нужный фильтр-прототип для данного ФНЧ₉:

• тип фильтра – С0350;

• ;

• ;

• с = 10.715101756;

• ;

• ;

• ;

• ;

• ;

• ;

• 

.

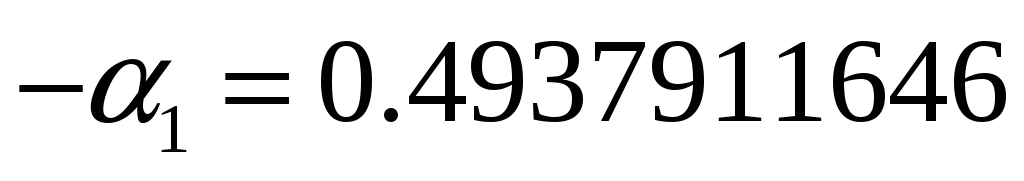Рис. 10.1 – Нормированная АЧХ ФНЧ₉

Рис. 10.2 – АЧХ ФНЧ₉

Рис. 11.1 – Нормированная ФЧХ ФНЧ₉

Рис. 11.2 – ФЧХ ФНЧ₉

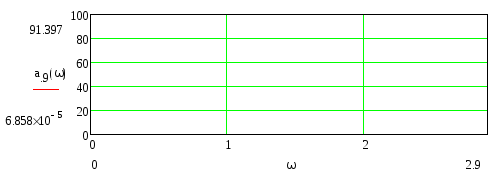
Рис. 12.1 – Нормированная ХРЗ ФНЧ₉

Рис. 12.2 – ХРЗ ФНЧ₉

Процедура 3:

а). Проанализируем математическую модель

Согласно варианту U_вх(t) примет следующий вид:

Построим график U_вх(t):

Рис. 13 – Входной сигнал

б). Построим лапласовское изображение измерительного сигнала :

Учтём, что .

.

cos x перепишем по формуле Эйлера: .

.

14