
ЦФУ
.docxЗадача 1
Представление чисел в различных системах счисления.
-
Представить десятичное число 1662 в двоичной, восьмеричной и шестнадцатеричной форме.
|
1662 |
2 |
|
|
|
|
|
|
|
|
|
|
1662 |
831 |
2 |
|
|
|
|
|
|
|
|
|
0 |
830 |
415 |
2 |
|
|
|
|
|
|
|
|
|
1 |
414 |
207 |
2 |
|
|
|
|
|
|
|
|
|
1 |
206 |
103 |
2 |
|
|
|
|
|
|
|
|
|
1 |
102 |
51 |
2 |
|
|
|
|
|
|
|
|
|
1 |
50 |
25 |
2 |
|
|
|
|
|
|
|
|
|
1 |
24 |
12 |
2 |
|
|
|
|
|
|
|
|
|
1 |
12 |
6 |
2 |
|
|
|
|
|
|
|
|
|
0 |
6 |
3 |
2 |
|
|
|
|
|
|
|
|
|
0 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
166210 = 110011111102
|
1662 |
8 |
|
|
|
1656 |
207 |
8 |
|
|
6 |
200 |
25 |
8 |
|
|
7 |
24 |
3 |
|
|
|
1 |
|
166210 = 31768
|
1662 |
16 |
|
|
1648 |
103 |
16 |
|
14 |
96 |
6 |
|
|
7 |
|
166210 = 67E16
-
Представить шестнадцатеричное число 62A в двоичной форме.
Для перевода из шестнадцатеричной системы счисления в двоичную надо каждую цифру исходного числа заменить соответствующей тетрадой двоичных цифр: 6 – 0110, 2 – 0010, A - 1010
62A = 110001010102
Задача 2
Описание и минимизация логических функций
Таблица истинности логических функций y1, y2, y3 :


Представим логическую функцию y1 в СДНФ:
y1
=



 +
+
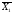


 +
+



 +
+



Минимизируем функцию y1 с помощью карт Карно.
|
x 1x2 |
x 3x4 |
|||
|
00 |
01 |
11 |
10 |
|
|
00 |
|
|
|
1 |
|
01 |
|
|
1 |
|
|
11 |
|
1 |
|
1 |
|
10 |
|
|
|
|
y1
=



 +
+



 +
+

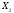

 +
+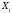


 =
=

 (
(

 +
+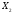
 )
+
)
+
 (
(
 +
+
 )
=
)
=

 (
( t
t )
+ +
)
+ +
 (
(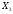 t
t )
)
Представим логическую функцию y1 в СКНФ
y1
= ( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+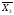 +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
(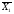 +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
)
Представим логическую функцию y2 в СДНФ:
y2
=



 +
+



 +
+



 +
+



 +
+



 +
+
![]()
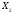


Минимизируем функцию y2 с помощью карт Карно.
|
x 1x2 |
x 3x4 |
|||
|
00 |
01 |
11 |
10 |
|
|
00 |
|
|
|
|
|
01 |
|
1 |
|
1 |
|
11 |
1 |
|
|
|
|
10 |
1 |
1 |
|
|
y2
=


 +
+



 +
+



 +
+


 +
+


 =
=
=
 (
( t
t
 )
+
)
+



 +
+


 +
+



Представим логическую функцию y2 в СКНФ:
y2
= ( +
+ +
+ +
+ )
(
)
( +
+ +
+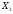 +
+ )
(
)
(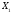 +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+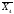 )
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
(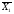 +
+ +
+ +
+ )
(
)
( +
+ +
+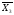 +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
)
Представим логическую функцию y3 в СДНФ:
y3
=

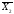

 +
+



 +
+



 +
+
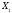


 +
+



 +
+



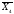
Минимизируем функцию y3 с помощью карт Карно.
|
x 1x2 |
x 3x4 |
|||
|
00 |
01 |
11 |
10 |
|
|
00 |
|
1 |
|
|
|
01 |
|
|
|
1 |
|
11 |
1 |
|
|
1 |
|
10 |
|
1 |
1 |
|
y3
=


 +
+

 +
+


 +
+


 =
=

 (
( +
+
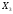 )
+
)
+
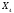
 (
(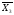 +
+
 )
)
Представим логическую функцию y3 в СКНФ
y3
= (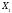 +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+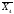 )
(
)
( +
+ +
+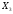 +
+ )
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+ +
+ )
(
)
( +
+ +
+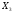 +
+ )
(
)
( +
+ +
+ +
+ )
)
( +
+ +
+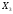 +
+ )
(
)
( +
+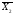 +
+ +
+ )
)
Комбинационная схема, реализующая функции y1, y2, y3 представлена на Error: Reference source not found.

Рисунок 1 – Комбинационная схема, реализующая функции y1, y2, y3.
Задача 3
Анализ работы комбинационной схемы.

С учётом того, что I63= D , при D=0 I63= 1 , значит = Y = 0.
При D=1 I63=0 и значение Q6 = Y будет зависеть от I61 и I62.
Так как сигнал со входа А появляется только на одном выходе мультиплексора, то на остальных выходах мультиплексора установятся логические нули. Значит либо I31= 0 и I32= 0, либо I41= 0 и I42= 0. Отсюда следует, что либо Q3= I61=1, либо Q4= I62=1, так как Q3= I31 + I32 и Q4= I41 tI42 . Значит Y=0.
Значит Y=0 при всех значениях переменных A,B,C,D.
Задача 4
Синтез последовательной схемы.
Синтезировать
синхронный счётчик на базе T
- триггеров, реализующий граф переходов
0 2 3 5 6 7 0.





Запрещённые состояния счётчика 1 и 4. Потребуем, чтобы из этого состояния счётчик переходил в состояние 0.
Таблица переходов проектируемого счётчика будет выглядеть следующим образом (Таблица 1).
Таблица 1
|
Q2 |
Q1 |
Q0 |
Q*2 |
Q*1 |
Q*0 |
T2 |
T1 |
T0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |











