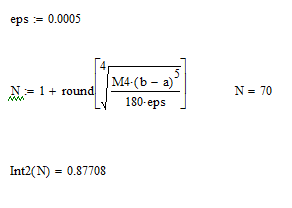ВАРИАНТ № 24
Задача 1. Элементы теории погрешностей.
Найти произведение приближенных чисел и указать его погрешности (Δ и δ), если считать в исходных данных все значащие цифры верными.
![]()
Решение.
По условию:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Вычисляем:
![]() .
.
Максимальное значение произведения:
![]() .
.
Минимальное значение произведения:
![]() .
.
Вычисляем абсолютную погрешность произведения:
![]() .
.
Относительная погрешность:
![]() .
.
Ответ.
![]() ,
,
![]() .
.
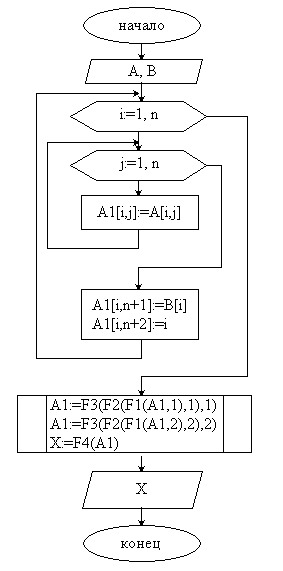
Задача 2. Численные методы решения систем линейных алгебраических уравнений (СЛАУ).
а) Найти решение СЛАУ
![]() ,
где
,
где
![]() – матрица коэффициентов,
– матрица коэффициентов,
![]() – вектор свободных членов,
– вектор свободных членов,
![]() – вектор неизвестных, методом Гаусса
(с выбором главного элемента по строке,
с выбором главного элемента по столбцу,
с выбором главного элемента по всей
матрице). Заданы матрица
– вектор неизвестных, методом Гаусса
(с выбором главного элемента по строке,
с выбором главного элемента по столбцу,
с выбором главного элемента по всей
матрице). Заданы матрица
![]() и вектор
и вектор
![]() .
При поиске решения (в MathCAD)
показать все промежуточные вычисления
в прямом и обратном ходе указанных
прямых методов. Полученное (приближенное)
решение сравнить с решением этой СЛАУ
в MathCAD вычислительным
блоком Given…find
(расчет провести в численном виде).
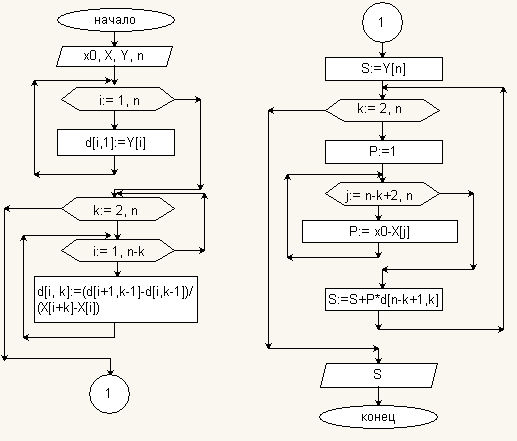
Зарисовать блок-схему алгоритма
указанного в варианте метода решения
СЛАУ при условии произвольного количества
уравнений (задаются матрица и вектор
).
.
При поиске решения (в MathCAD)
показать все промежуточные вычисления
в прямом и обратном ходе указанных
прямых методов. Полученное (приближенное)
решение сравнить с решением этой СЛАУ
в MathCAD вычислительным
блоком Given…find
(расчет провести в численном виде).
Зарисовать блок-схему алгоритма
указанного в варианте метода решения
СЛАУ при условии произвольного количества
уравнений (задаются матрица и вектор
).
 ,
,
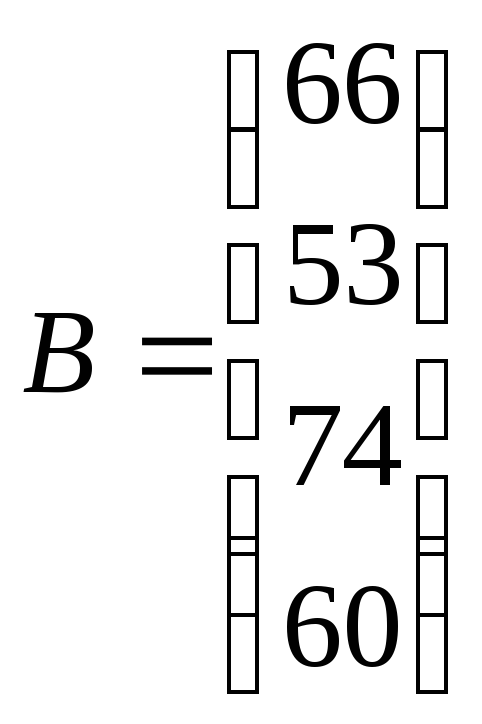
Решение.
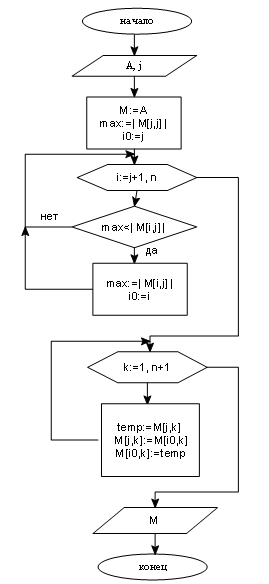
Блок-схема алгоритма – решение СЛАУ методом Гаусса с выбором главного элемента по всей матрице:
- функция
![]() ,
с помощью которой выбираем главный
элемент по столбцу и меняем строки:
,
с помощью которой выбираем главный
элемент по столбцу и меняем строки:
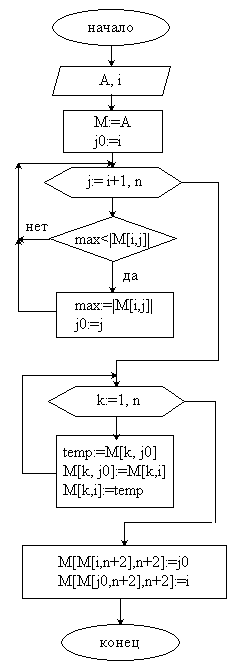
- функция
![]() ,
с помощью которой выбираем главный
элемент по строке и меняем столбцы и
перенумеровываем переменные:
,
с помощью которой выбираем главный
элемент по строке и меняем столбцы и
перенумеровываем переменные:
- шаг прямого хода метода Гаусса (![]() )
и обратный ход метода Гаусса (
)
и обратный ход метода Гаусса (![]() ):
):
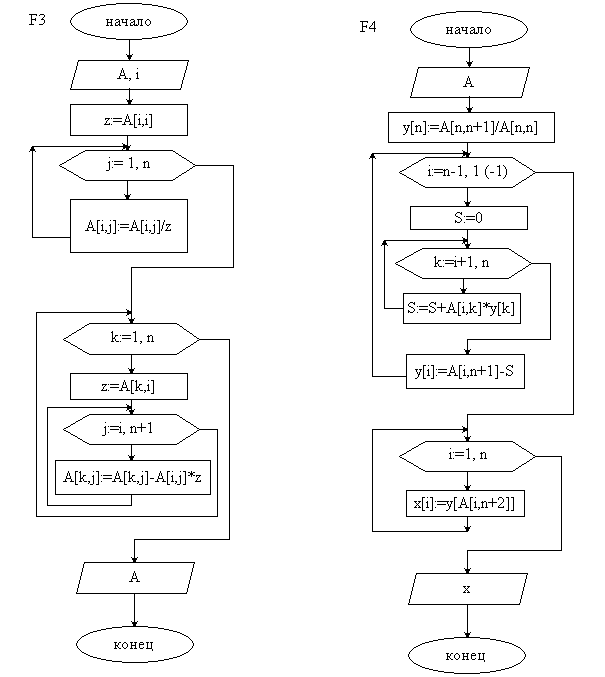
- главная программа:
Последовательность вычислений:




Решение задачи в MathCAD с помощью блока Given..Find:

Задача 3. Приближение функций.
Часть 1.
в) По заданным узловым значениям
исходной функции (векторы и
![]() )
осуществить интерполяцию с помощью
интерполяционного полиномома Ньютона
)
осуществить интерполяцию с помощью
интерполяционного полиномома Ньютона
![]() (вид записи - интерполяция назад).
(вид записи - интерполяция назад).
Построить в MathCAD в одном графическом шаблоне полученный интерполяционный полином и узловые значения исходной функции.
Зарисовать блок-схему алгоритма,
реализующего вычисление значения
интерполяционного полинома Ньютона
(назад) в любом значении аргумента ![]() при условии произвольного количества
узловых значений исходной функции.
при условии произвольного количества
узловых значений исходной функции.
Часть 2.
По заданным узловым значениям исходной
функции (векторы и
![]() )
записать систему линейных алгебраических
уравнений для расчета коэффициентов
кубического сплайна со свободным
закреплением концов. Решить полученную
систему в MathCAD вычислительным
блоком Given…find,
записать функцию
)
записать систему линейных алгебраических
уравнений для расчета коэффициентов
кубического сплайна со свободным
закреплением концов. Решить полученную
систему в MathCAD вычислительным
блоком Given…find,
записать функцию
![]() ,
реализующую рассчитанный кубический
сплайн, считая, что за границами
рассматриваемого диапазона изменения
аргумента изменение функции
,
реализующую рассчитанный кубический
сплайн, считая, что за границами
рассматриваемого диапазона изменения
аргумента изменение функции
![]() осуществляется соответственно по
начальному и конечному частям сплайна.
Построить в одном графическом шаблоне
рассчитанный кубический сплайн и узловые
значения исходной функции.
осуществляется соответственно по
начальному и конечному частям сплайна.
Построить в одном графическом шаблоне
рассчитанный кубический сплайн и узловые
значения исходной функции.
Часть 3.
По заданным узловым значениям исходной
функции (векторы и
![]() )
методом наименьших квадратов построить
аппроксимирующий многочлен , где
)
методом наименьших квадратов построить
аппроксимирующий многочлен , где
φi(x)=xi.
Условия построения аппроксимирующего
многочлена методом наименьших квадратов
дают систему линейных алгебраических
уравнений (в количестве m+1)
относительно неизвестных
![]() .
Записать указанную систему уравнений
и решить её в MathCAD с помощью
вычислительного блока Given…find.
Отобразить в одном графическом шаблоне
полученный аппроксимирующий многочлен
Pm(x)
и узловые значения исходной функции.
Рассчитать величину
.
Записать указанную систему уравнений
и решить её в MathCAD с помощью
вычислительного блока Given…find.
Отобразить в одном графическом шаблоне
полученный аппроксимирующий многочлен
Pm(x)
и узловые значения исходной функции.
Рассчитать величину
![]() (среднеквадратичного
отклонения) для полученного аппроксимирующего
обобщённого многочлена.
(среднеквадратичного
отклонения) для полученного аппроксимирующего
обобщённого многочлена.
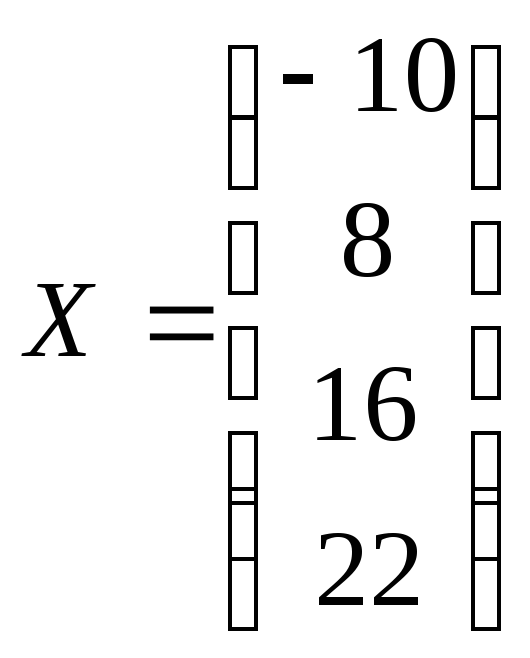 ,
,
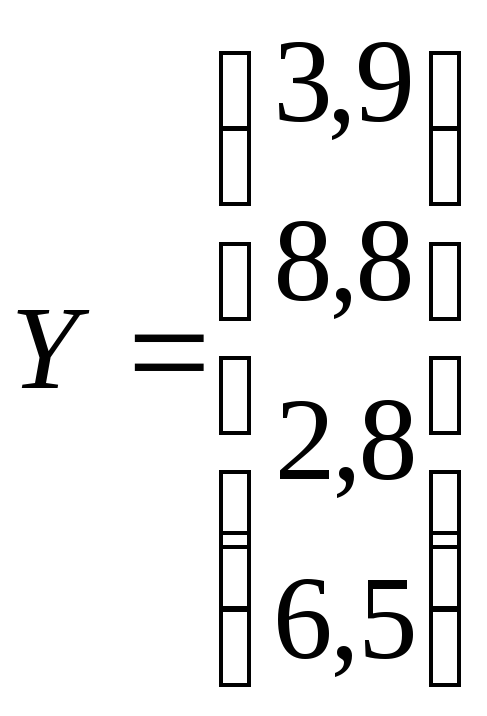 ,
,
![]() ,
,
Часть 4.
Для указанной функции g(x)
и рассматриваемого интервала
![]() сформировать
в MathCAD в виде ранжированных
переменных N отсчётных
значений X1l
и Y1l=g(X1l)
(l=
сформировать
в MathCAD в виде ранжированных
переменных N отсчётных
значений X1l
и Y1l=g(X1l)
(l=![]() ,
h – шаг между точками в
интервале
,
h – шаг между точками в
интервале
![]() .
Выполнить следующие виды приближений
таблично заданной функции при условии:
.
Выполнить следующие виды приближений
таблично заданной функции при условии:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
lnfit
,
lnfit
а) Реализовать в MathCAD по рассчитанным узловым значениям (векторы X1 и Y1) кусочно-линейную интерполяцию (функция linterp), кубическую сплайновую с различным продолжением (функции lspline, pspline, cspline, interp). Отобразить в одном графическом шаблоне исходную функцию g(x), узловые значения (векторы X1 и Y1) и четыре полученные интерполяционные функции.
б) По узловым значениям (векторы X1 и Y1) реализовать в MathCAD В-сплайн интерполяцию с различными степенями заменяющих полиномов (n=1,2,3), выбрав самостоятельно векторы точек сшивок U. В одном графическом шаблоне отобразить исходную функцию g(x) , узловые значения (векторы X1 и Y1), три интерполяционные функции В-сплайнов и соответствующие им точки сшивок.
в) По узловым значениям (векторы
X1 и Y1)
реализовать в MathCAD линейную
аппроксимацию (функции line,
medfit), полиномиальную
аппроксимацию (функцию regress
(в задании даны степени аппроксимирующих
полиномов) и loess
(параметр span выбрать
самостоятельно)), аппроксимацию функциями
специального вида ( в задании указана
lnfit ). Отобразить в
одном графическом шаблоне исходную
функцию g(x),
узловые значения (векторы X1
и Y1) и полученные
аппроксимирующие функции; для всех
аппроксимирующих функций рассчитать
величину среднеквадратичного отклонения
(![]() ).
).
Решение.
Строим интерполяционный полином Ньютона (вид записи – интерполяция назад):
![]() .
.
Разделенными разностями первого порядка, составленными по соседним узлам, называют отношения
![]()
По ним можно определить разделенные разности второго порядка
![]()
Аналогично определяются разделенные
разности более высокого порядка.
Например, если известны разделенные
разности
![]() -го
порядка, то разделенная разность
-го
порядка, то разделенная разность
![]() -го
порядка определяется как
-го
порядка определяется как
![]() .
.
Вычисления производим в MathCAD:

Построим в MathCAD в одном графическом шаблоне полученный интерполяционный полином и узловые значения исходной функции.
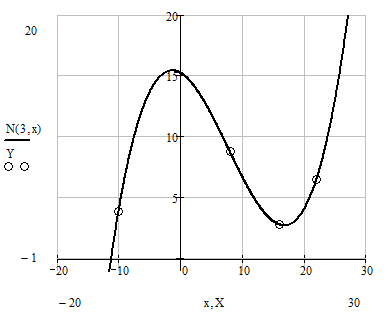
Блок-схема алгоритма, реализующего
вычисление значения интерполяционного
полинома Ньютона (назад) в любом значении
аргумента
![]() при условии произвольного количества
узловых значений исходной функции:
при условии произвольного количества
узловых значений исходной функции:
По заданным узловым значениям исходной
функции (векторы и
![]() )
запишем СЛАУ для расчета коэффициентов
кубического сплайна со свободным
закреплением концов.
)
запишем СЛАУ для расчета коэффициентов
кубического сплайна со свободным
закреплением концов.
Известно, что при кубическом сплайне между парой соседних узлов интерполяции имеем кубический многочлен вида
![]()
Для определения коэффициентов
![]() ,
,
![]() ,
,
![]() ,
,
![]() на всех
на всех
![]() отрезках записывают и решают
отрезках записывают и решают
![]() линейных уравнений из условия непрерывности
функции
линейных уравнений из условия непрерывности
функции
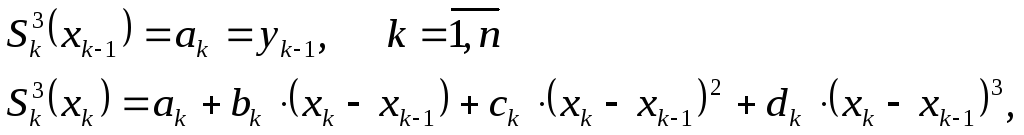
непрерывности первых и вторых производных в узлах интерполяции
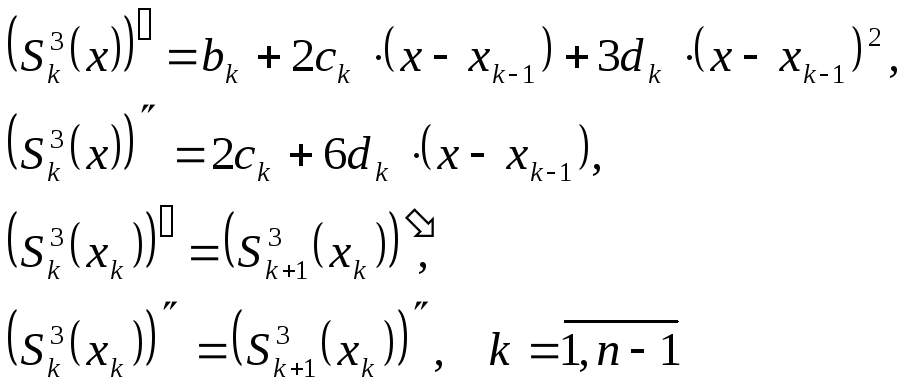
и условия свободного закрепления концов
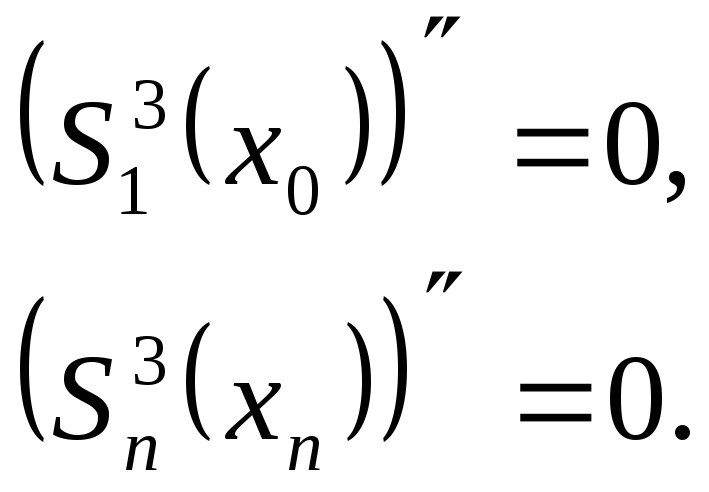
В нашем случае имеем:

Решаем эту систему в MathCAD вычислительным блоком Given…find:
![]()
Получаем:

Запишем функцию
![]() ,
реализующую рассчитанный кубический
сплайн, считая, что за границами
рассматриваемого диапазона изменения
аргумента изменение функции
,
реализующую рассчитанный кубический
сплайн, считая, что за границами
рассматриваемого диапазона изменения
аргумента изменение функции
![]() осуществляется соответственно по
начальному и конечному частям сплайна:
осуществляется соответственно по
начальному и конечному частям сплайна:
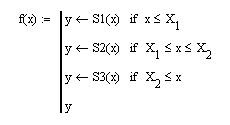
Построим в одном графическом шаблоне рассчитанный кубический сплайн и узловые значения исходной функции:
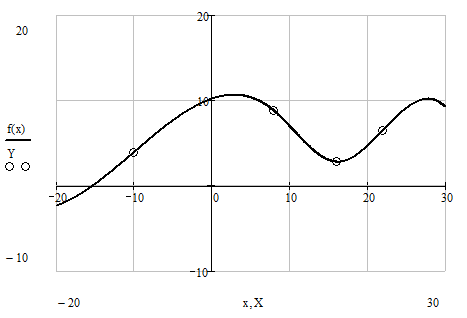
По заданным узловым значениям исходной
функции (векторы и
![]() )
методом наименьших квадратов определим
коэффициенты аппроксимирующего
обобщенного многочлена , где φi(x)
- система базисных функций (в задании
даны степенные функции xi
). Согласно метода наименьших квадратов
коэффициенты
)
методом наименьших квадратов определим
коэффициенты аппроксимирующего
обобщенного многочлена , где φi(x)
- система базисных функций (в задании
даны степенные функции xi
). Согласно метода наименьших квадратов
коэффициенты
![]() определяются
из условия
определяются
из условия
![]() . (1)
. (1)
При поиске минимального значения
![]() необходимое
и достаточное условие
необходимое
и достаточное условие
![]() (2)
(2)
дает систему из ![]() линейных алгебраических уравнений
относительно неизвестных
линейных алгебраических уравнений
относительно неизвестных ![]() .
Запишем систему (2) и решим ее в MathCAD
вычислительным блоком Given…find.
.
Запишем систему (2) и решим ее в MathCAD
вычислительным блоком Given…find.
Экстремальная задача примет вид:
![]() .
.
Параметры искомой зависимости находятся из системы:
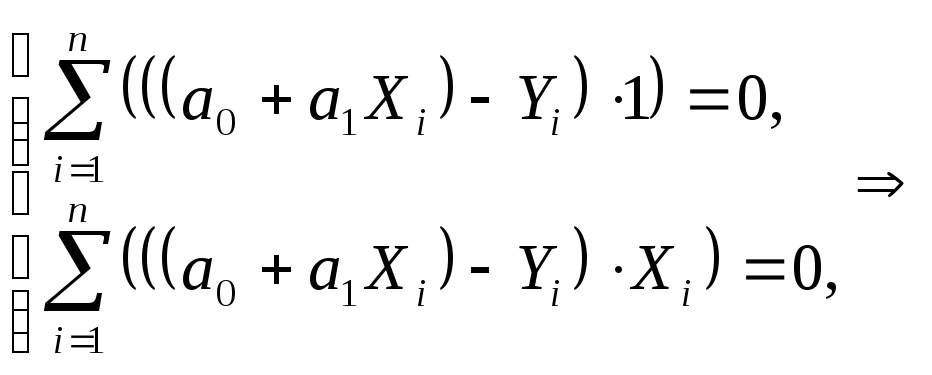
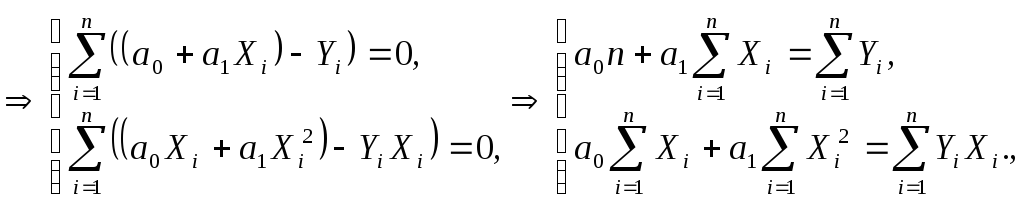
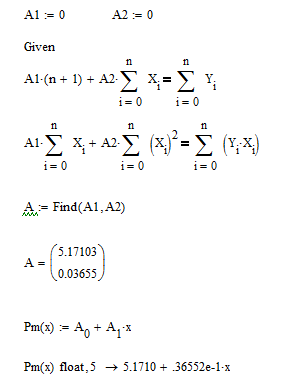
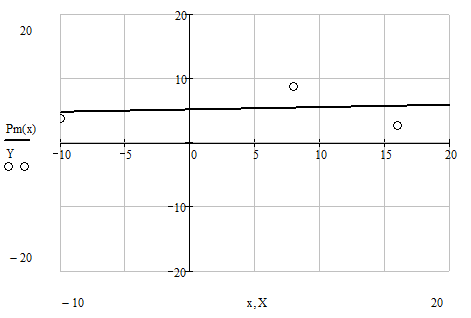
Отобразим в одном графическом шаблоне
полученный аппроксимирующий обобщенный
многочлен ![]() и узловые значения исходной функции:
и узловые значения исходной функции:
Величина ![]() для
полученного аппроксимирующего обобщенного
многочлена:
для
полученного аппроксимирующего обобщенного
многочлена:
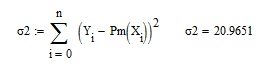
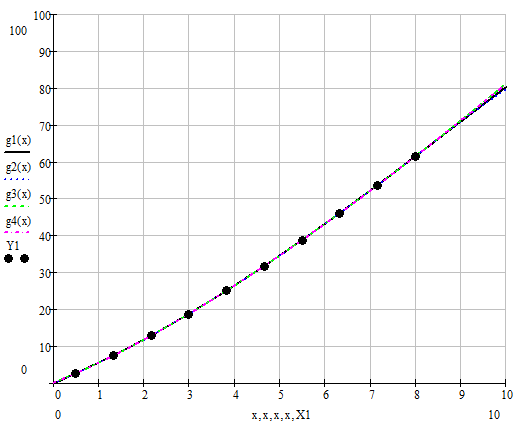
а) Реализуем в MathCAD по
рассчитанным узловым значениям (векторы
![]() и
и
![]() )
кусочно-линейную интерполяцию (функция
linterp), кубическую
сплайновую с различным продолжением
(функции lspline, pspline,
cspline, interp).
Отобразим в одном графическом шаблоне
исходную функцию
)
кусочно-линейную интерполяцию (функция
linterp), кубическую
сплайновую с различным продолжением
(функции lspline, pspline,
cspline, interp).
Отобразим в одном графическом шаблоне
исходную функцию
![]() ,
узловые значения (векторы
,
узловые значения (векторы
![]() и
и
![]() )
и четыре полученные интерполяционные
функции.
)
и четыре полученные интерполяционные
функции.

б) По узловым значениям (векторы
![]() и
и
![]() )
реализовать в MathCAD В-сплайн
интерполяцию с различными степенями
заменяющих полиномов (
)
реализовать в MathCAD В-сплайн
интерполяцию с различными степенями
заменяющих полиномов (![]() ),
выбрав самостоятельно векторы точек
сшивок
),
выбрав самостоятельно векторы точек
сшивок
![]() .
В одном графическом шаблоне отобразить
исходную функцию , узловые значения
(векторы
.
В одном графическом шаблоне отобразить
исходную функцию , узловые значения
(векторы
![]() и
и
![]() ),
три интерполяционные функции В-сплайнов
и соответствующие им точки сшивок.
),
три интерполяционные функции В-сплайнов
и соответствующие им точки сшивок.

Графики:
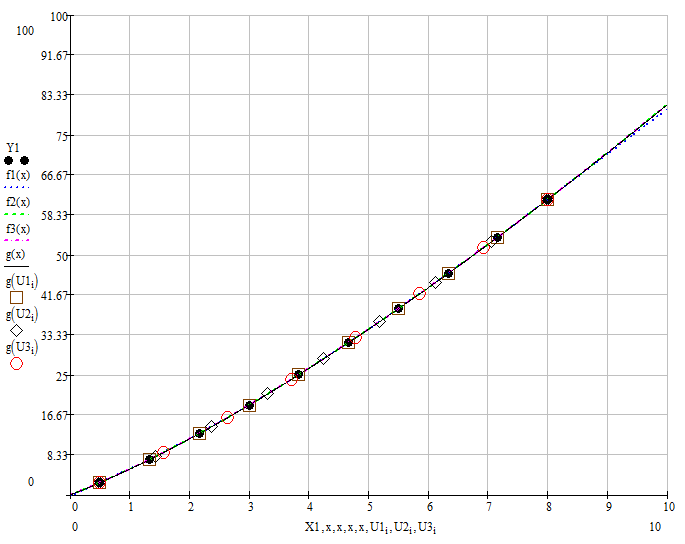
в) По узловым значениям (векторы
![]() и
и
![]() )
реализуем в MathCAD линейную
аппроксимацию (функции line,
medfit), полиномиальную
аппроксимацию (функции regress
(в задании даны степени аппроксимирующих
полиномов) и loess
(параметр span выбрать
самостоятельно)), аппроксимацию функциями
специального вида (в задании указана
из функция lnfit).
)
реализуем в MathCAD линейную
аппроксимацию (функции line,
medfit), полиномиальную
аппроксимацию (функции regress
(в задании даны степени аппроксимирующих
полиномов) и loess
(параметр span выбрать
самостоятельно)), аппроксимацию функциями
специального вида (в задании указана
из функция lnfit).
Для всех аппроксимирующих функций
рассчитаем величину среднеквадратичного
отклонения (![]() ).
).

Отобразим в одном графическом шаблоне
исходную функцию , узловые значения
(векторы
![]() и
и
![]() )
и полученные аппроксимирующие функции.
)
и полученные аппроксимирующие функции.

Задача 4. Численное интегрирование функций.
В MathCAD вычислить
интеграл ![]() указанным численным методом – методом
Симпсона при заданном количестве
указанным численным методом – методом
Симпсона при заданном количестве
![]() разбиений интервала интегрирования
разбиений интервала интегрирования
![]() (шаг интегрирования
(шаг интегрирования ![]() )
и оценить погрешность применения данной
составной квадратурной формулы.
)
и оценить погрешность применения данной
составной квадратурной формулы.
Для вычисления интеграла по указанному
методу написать в MathCAD
функцию пользователя, в которой входным
параметром является количество ![]() разбиений интервала интегрирования,
имя подынтегральной функции и пределы
интегрирования. Отобразить функции
разбиений интервала интегрирования,
имя подынтегральной функции и пределы
интегрирования. Отобразить функции
![]() ,
,
![]() и
и ![]() (в соответствии с применяемыми методами)
на интервале
(в соответствии с применяемыми методами)
на интервале ![]() .
По оценке погрешности составной
квадратурной формулы интегрирования
указанным методом рассчитать количество
требуемых интервалов разбиения для
вычисления интеграла с заданной точностью
ε. Вычислить интеграл с этой точностью.
.
По оценке погрешности составной
квадратурной формулы интегрирования
указанным методом рассчитать количество
требуемых интервалов разбиения для
вычисления интеграла с заданной точностью
ε. Вычислить интеграл с этой точностью.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Решение.
Разбиение интервала задается следующим образом:
![]()
![]() .
.
Для вычисления интеграла методом Симпсона воспользуемся формулой:
![]()
Составим в MathCAD функцию пользователя и вычислим интеграл при разных количествах разбиений:
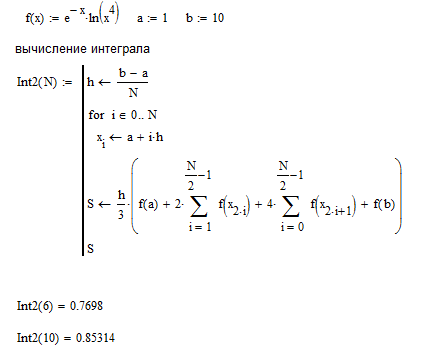
В методе Симпсона (по удвоенным частичным отрезкам) – оценка погрешности соответственно
![]() ,
,
где ![]() .
.
Вычисляем максимальное значение модуля четвертой производной на данном отрезке:
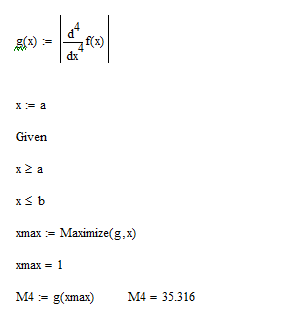
Оценки погрешности для каждого
![]() :
:
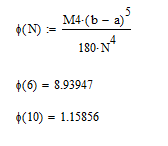
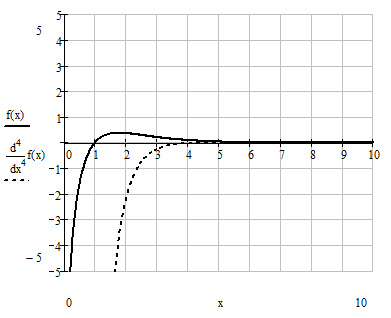
Строим графики функций
![]() и
и
![]() :
:
Находим необходимое количество интервалов для достижения заданной точности: