
Сложные функции.
Определение.
Пусть даны функции
![]() .
Функция вида
.
Функция вида
![]() называется сложной (композицией) функции
на функцию
называется сложной (композицией) функции
на функцию
![]() .
.
Чтобы
найти значение сложной функции
![]() ,
сначала необходимо по независимой
переменной
вычислить значение
,
сначала необходимо по независимой
переменной
вычислить значение
![]() ,
а затем по найденному значению
найти значение
,
а затем по найденному значению
найти значение
![]() .
При этом функцию
называют внутренней функцией композиции,
а функцию
– внешней функцией композиции.
.
При этом функцию
называют внутренней функцией композиции,
а функцию
– внешней функцией композиции.
Правила построения графиков функций.
Пусть задан график функции . Справедливы правила:
График функции
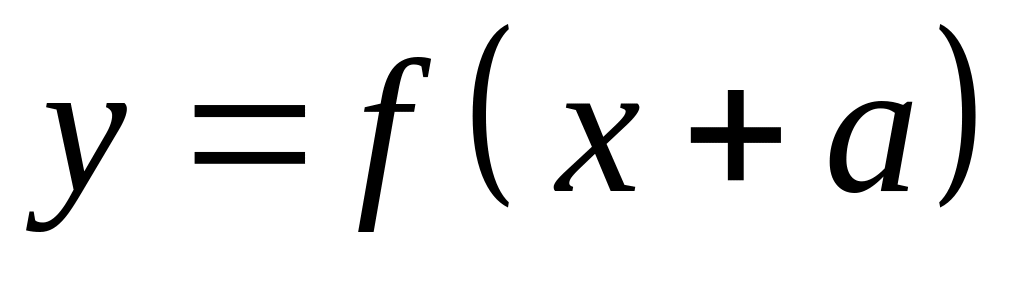 есть график функции
,
сдвинутый (при
есть график функции
,
сдвинутый (при
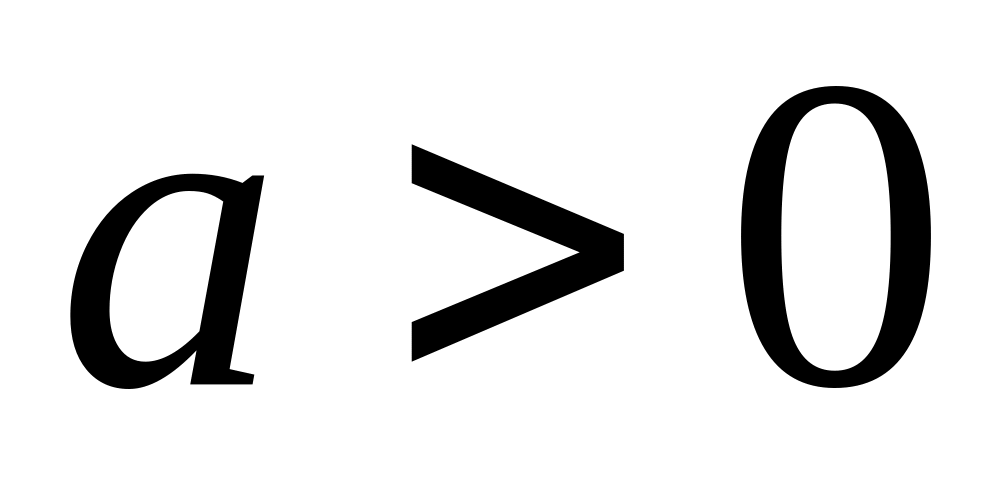 влево, при
вправо) на
влево, при
вправо) на
 единиц
параллельно оси
.
единиц
параллельно оси
.График функции
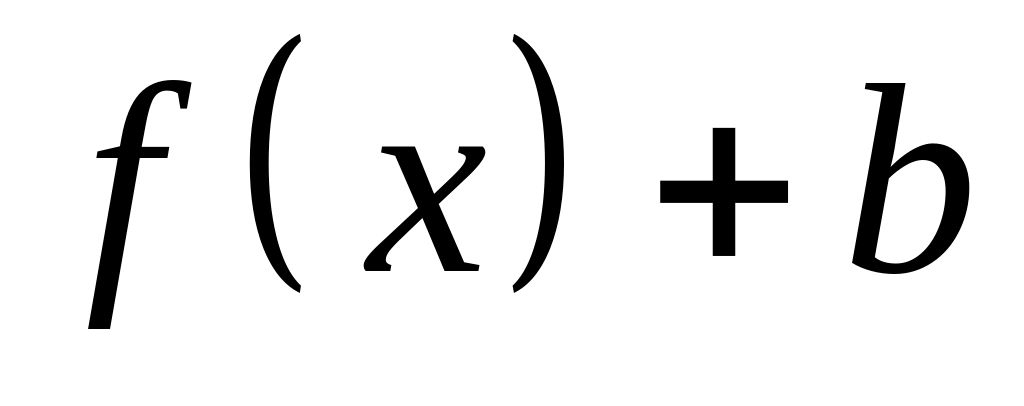 есть
график функции
,
сдвинутый (при
есть
график функции
,
сдвинутый (при
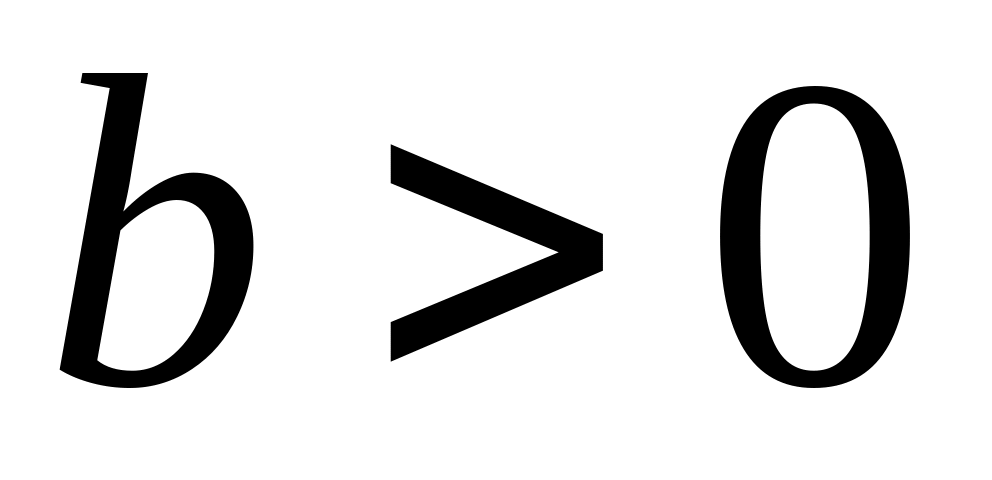 вверх, при
вверх, при
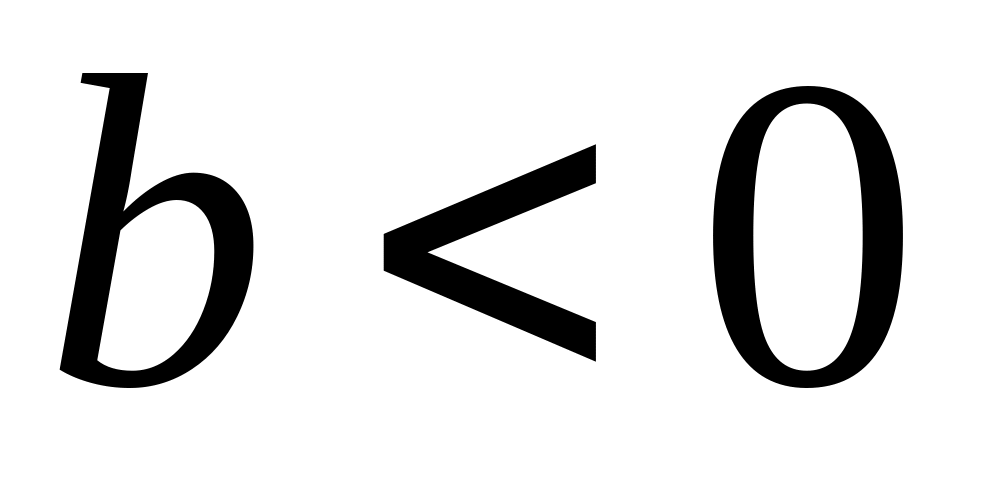 вниз)
на
вниз)
на
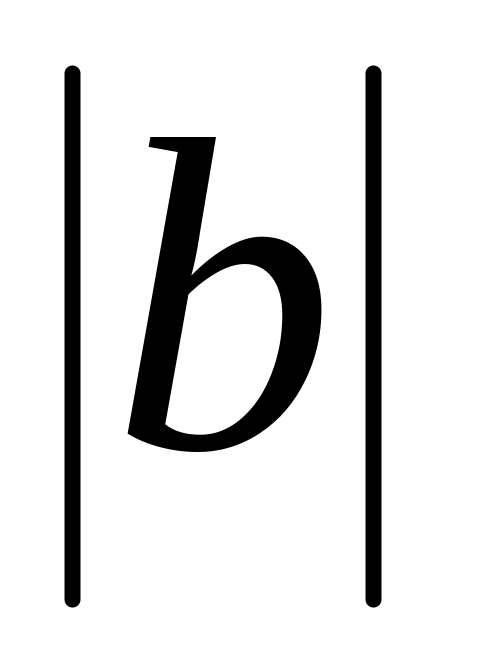 единиц параллельно оси
единиц параллельно оси
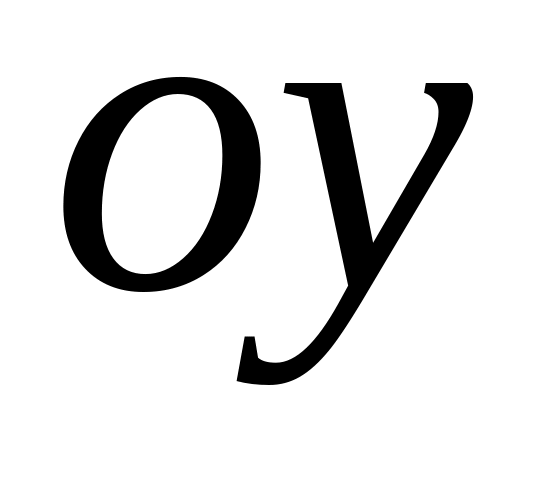 .
.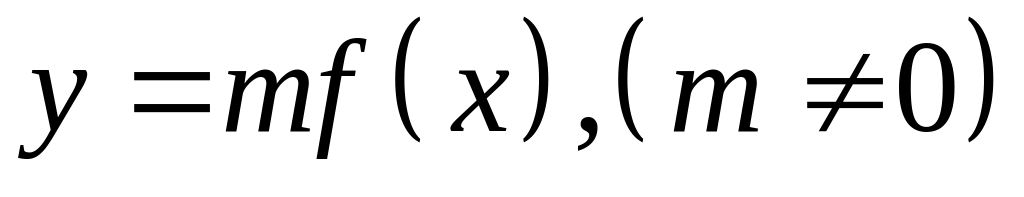 есть график функции
,
растянутый (при
есть график функции
,
растянутый (при
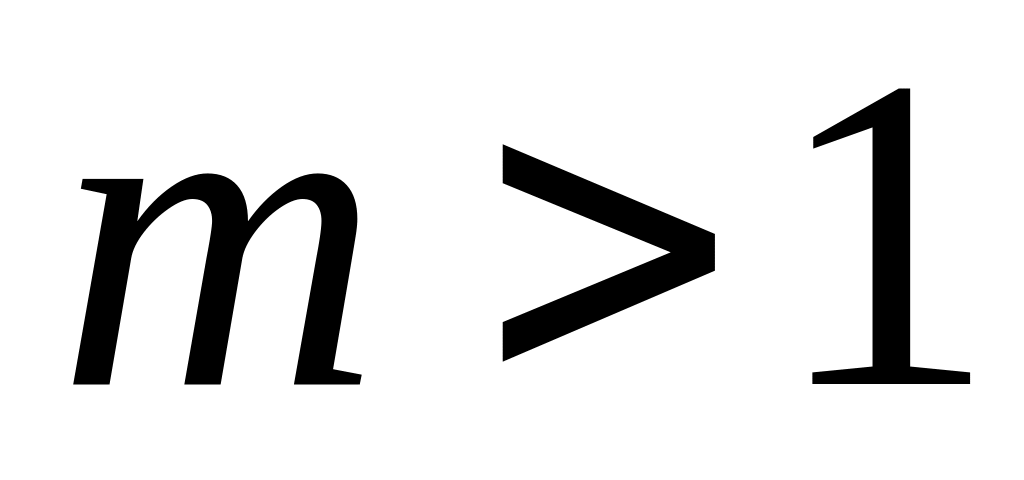 )
в
)
в
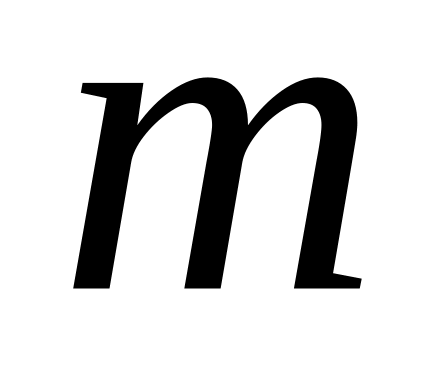 раз и сжатый (при
раз и сжатый (при
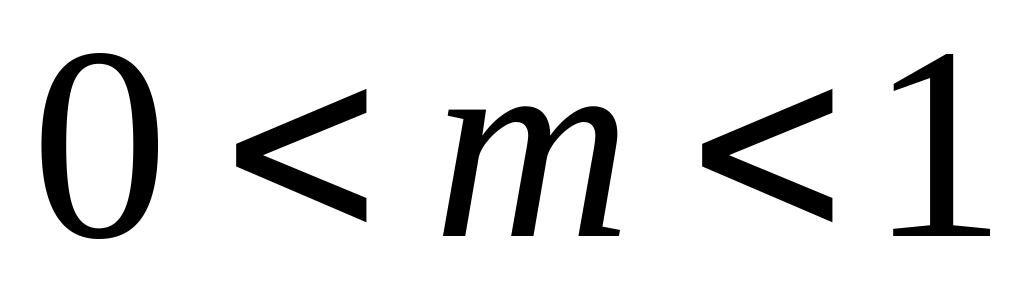 )
вдоль оси
.
)
вдоль оси
.
При
![]() график функции – зеркальное отображение
графика функции
график функции – зеркальное отображение
графика функции
![]() от оси
.
от оси
.
4.
![]() -
график функции
,
сжатый в k
раз при
-
график функции
,
сжатый в k
раз при
![]() вдоль оси
.
При
график функции
-
зеркальное отображение графика функции
вдоль оси
.
При
график функции
-
зеркальное отображение графика функции
![]() от оси
.
от оси
.
Примеры.
I/Найти область определения функции .
1.
![]() .
.
Решение.
Функция представляет
собой сумму функций. Область определения
исходной функции состоит из всех значений
,
которые одновременно принадлежат
области определения функций
![]() и
и
![]() .
.
Область определения подкоренного выражения неотрицательна, а логарифмической функции – положительные числа,
то решим систему неравенств:
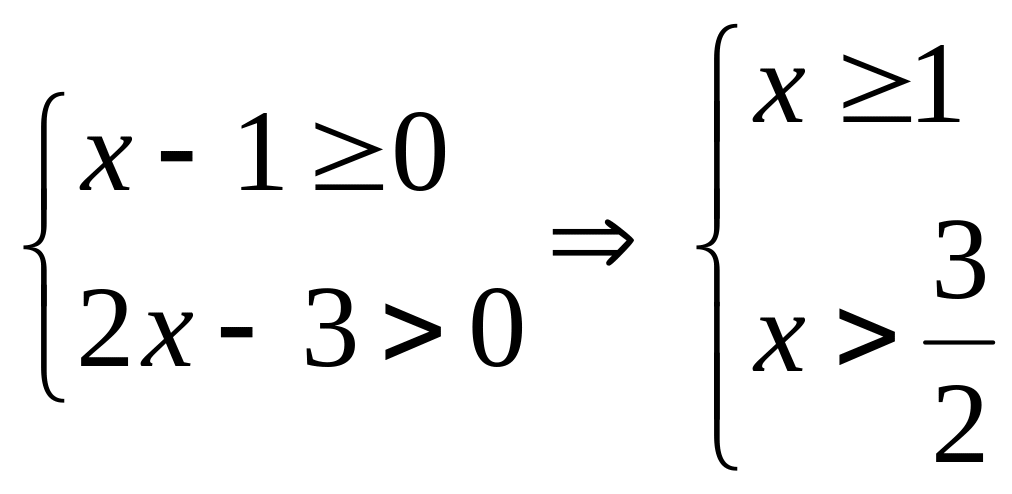
Отметим на числовом
луче точки
![]() и
и
![]() .
.
Следовательно,
область определения исходной функции:
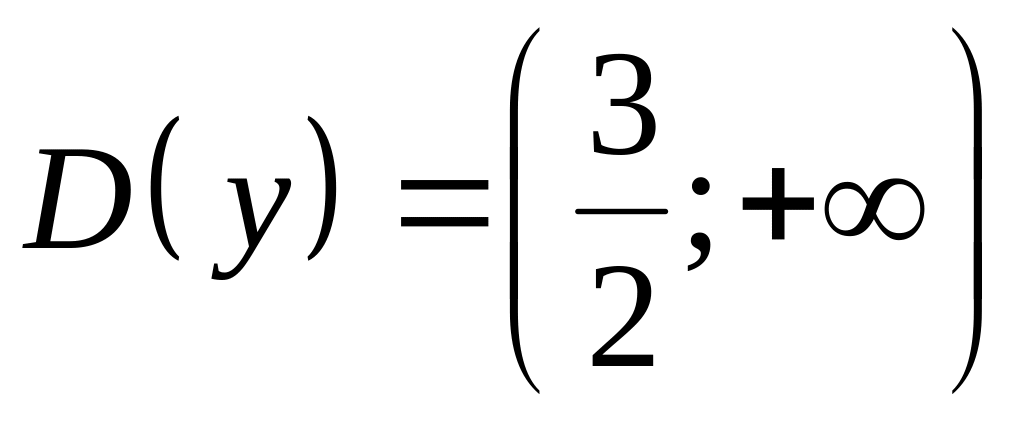 .
.
2.
![]() .
.
Решение.
Функция представляет
собой сумму функций. Область определения
исходной функции состоит из всех значений
,
которые одновременно принадлежат
области определения функций
![]() и
и
![]() .
.
 Область
определения логарифмической функции
– множество положительных чисел, а
значение подкоренного выражения
неотрицательное, то область определения
заданной функции определяется как
совокупность значений
,
при которых одновременно выполняются
неравенства
Область
определения логарифмической функции
– множество положительных чисел, а
значение подкоренного выражения
неотрицательное, то область определения
заданной функции определяется как
совокупность значений
,
при которых одновременно выполняются
неравенства
![]() и
и
![]() .
Решим систему неравенств:
.
Решим систему неравенств:
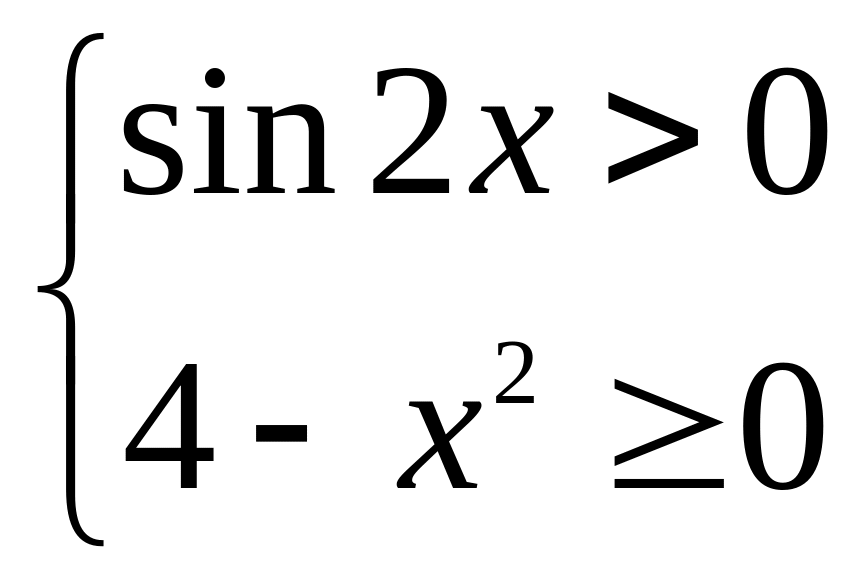
Т. к. функция
![]() положительная на промежутке
положительная на промежутке
![]() ,
то решим систему неравенств:
,
то решим систему неравенств:
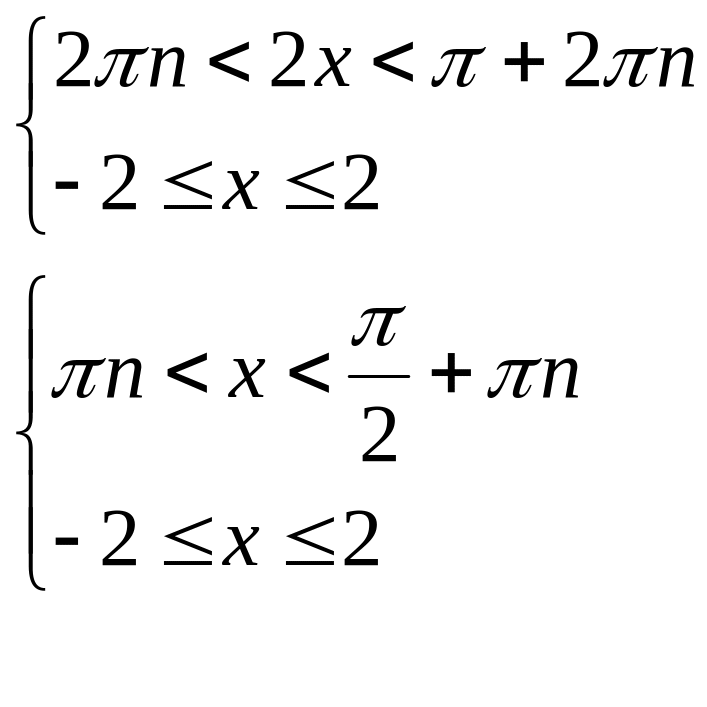
Следовательно, область определения исходной функции промежуток:
![]() .
.
3.
![]() .
.
Решение.
Oбласть
определения исходной функции – отрезок
![]() ,
поэтому справедливо неравенство:
,
поэтому справедливо неравенство:
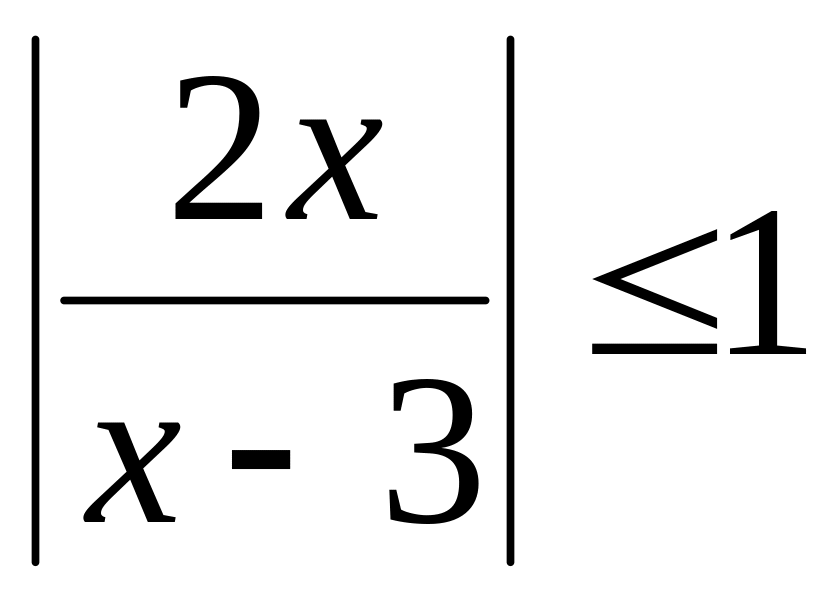 ,
решим двойное неравенство:
,
решим двойное неравенство:
![]() .
.
Перейдём к решению системы неравенств:
![]()
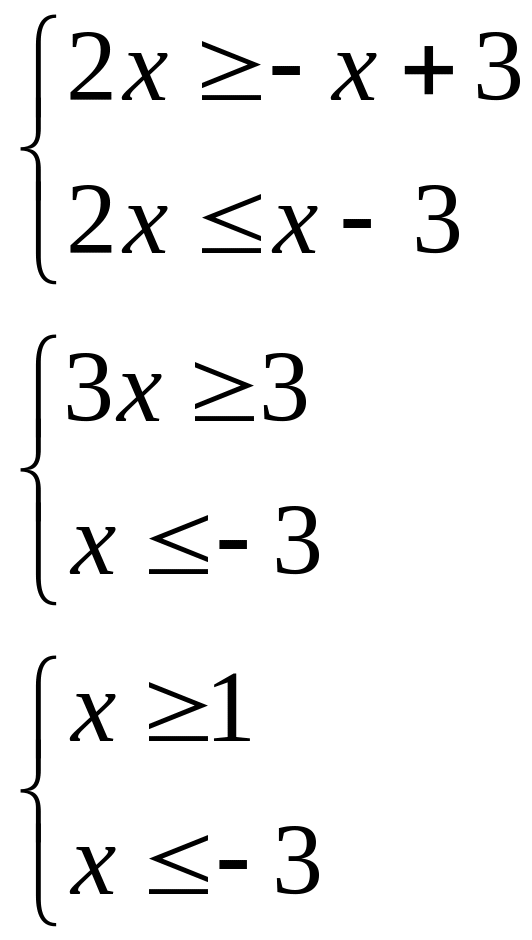
Следовательно,
областью определения функции
![]() является
является
объединение
промежутков
![]() .
.
4.
![]() .
.
Решение.
Функция представляет
собой сумму функций; область определения
исходной функции состоит из всех значений
,
которые одновременно принадлежат
области определения функций:
![]() ,
,
![]() и
и
![]() .
.
Область определения
логарифмической функции – множество
положительных чисел, а значение
подкоренного выражения неотрицательное,
областью определения функции
![]() является интервал
является интервал
![]() ,
то область определения заданной функции
определяется как совокупность значений
х, при которых одновременно выполняются
неравенства:
,
то область определения заданной функции
определяется как совокупность значений
х, при которых одновременно выполняются
неравенства:
![]() и
и
![]() .
.
Решим систему
уравнений:
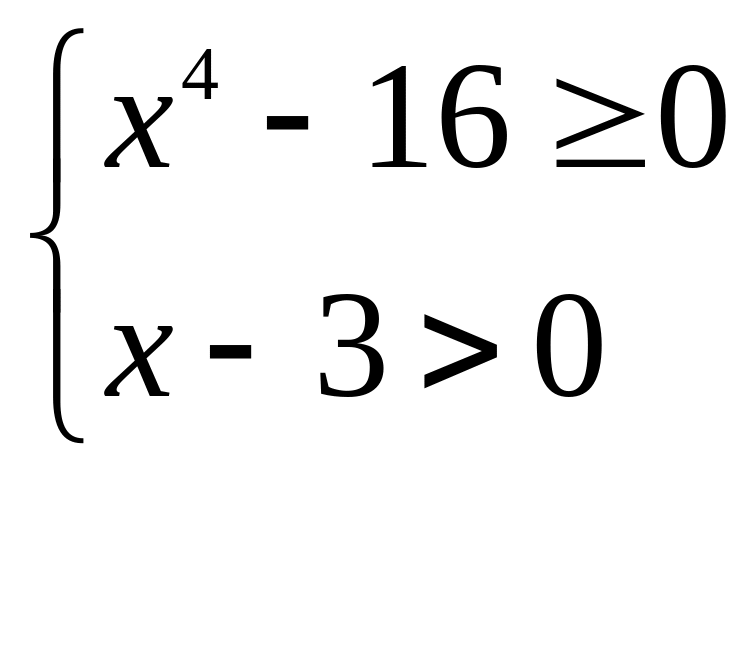
Областью определения
функции
![]() является объединение промежутков:
является объединение промежутков:
![]() .
Заметим, что области определения функций
и
.
Заметим, что области определения функций
и
![]() совпадают.
совпадают.
Для функции
![]() область определения -
область определения -
![]() .
Объединяя области определения всех
трёх функций, получим
.
Объединяя области определения всех
трёх функций, получим
![]() - область определения данной функции.
- область определения данной функции.
II.Построить графики функций:
1.![]()
Решение.
Проводим построение графика следующим образом:
1.Изобразим график
функции
![]() .
.
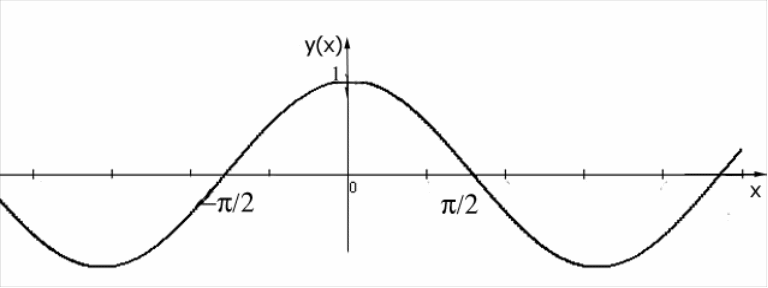
2.Изобразим график
функции
![]() ,
который получается сжатием графика
функции
вдоль оси
.
,
который получается сжатием графика
функции
вдоль оси
.

3.Начертим график
функции
![]() ,
который является зеркальным отображением
графика
относительно оси
.
,
который является зеркальным отображением
графика
относительно оси
.
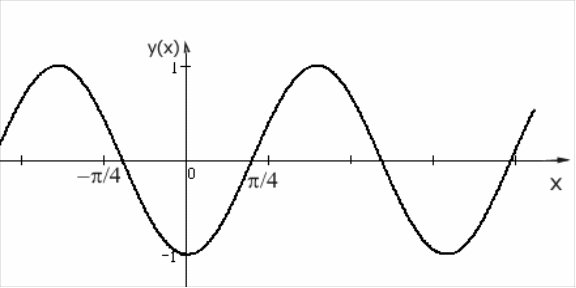
4.Построим график
функции
![]() ,
который получается растяжением в 3 раза
вдоль оси
графика функции
.
,
который получается растяжением в 3 раза
вдоль оси
графика функции
.

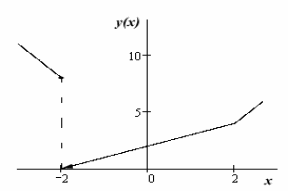
2.
![]() .
.
Решение.
- модуль (абсолютная величина) числа а определяется следующим:
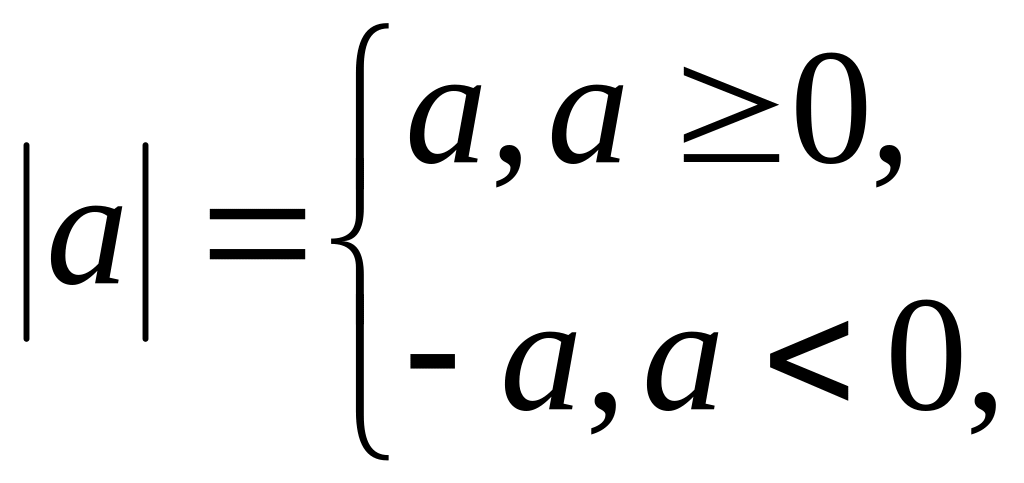
Первоначально
находим нули подмодульных выражений:
![]() и
и
![]() .
.
Это числа
![]() поэтому всю числовую ось разбиваем на
промежутки
поэтому всю числовую ось разбиваем на
промежутки
![]() .
На каждом из них по определению раскрываем
модули
.
На каждом из них по определению раскрываем
модули
![]() .
.
При
![]() имеем
имеем
![]() т. к.
т. к.
![]() ;
;
![]() ,
,
т. к.
![]() ,
то при
исходная функция примет вид:
,
то при
исходная функция примет вид:![]()
![]()
Затем при
![]() т. к.
т. к.
![]() т. к.
т. к.
![]() ,
то при
,
то при
![]() исходная функция примет вид:
исходная функция примет вид:
![]()
При
![]() имеем
имеем
![]() ,
т. к.
,
т. к.
![]() т.
к.
.
т.
к.
.
При
исходная
функция примет вид
![]() .
.
Для построения графика функцию запишем в кусочно – заданном виде
![]()

Теперь построим график этой функции.
3.
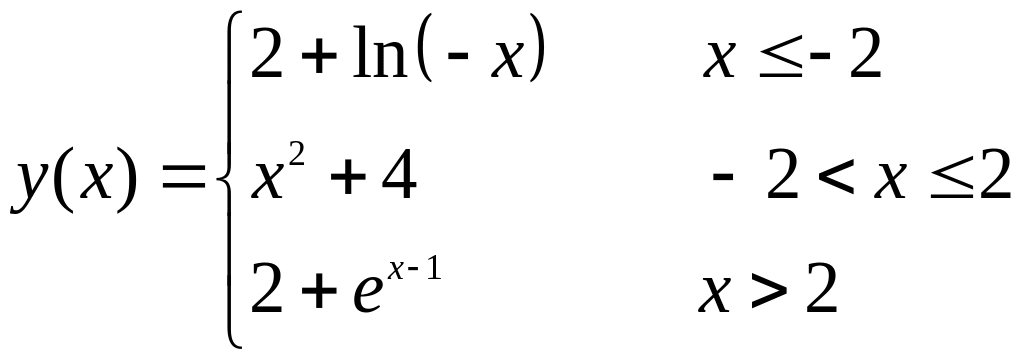
Решение.
Исследуемая функция
представлена в кусочно – заданном виде.
Построим сначала график функции
![]() .
Для этого построим график функции
.
Для этого построим график функции
![]() .
Он получается путём параллельного
переноса графика функции
.
Он получается путём параллельного
переноса графика функции
![]() вправо на одну единицу вдоль оси
вправо на одну единицу вдоль оси
![]() График функции
График функции
![]() получим путём сдвига на две единицы
вверх вдоль оси
графика функции
.
получим путём сдвига на две единицы
вверх вдоль оси
графика функции
.
Теперь построим
график функции
![]() Его
получаем путём сдвига вдоль оси
вверх на четыре единицы параболы. График
функции
Его
получаем путём сдвига вдоль оси
вверх на четыре единицы параболы. График
функции
![]() получен построением зеркального
отображения относительно оси
графика
функции
получен построением зеркального
отображения относительно оси
графика
функции
![]() .
Сдвигая на 2 единицы вверх по оси
график
функции
.
Сдвигая на 2 единицы вверх по оси
график
функции
![]() ,
получаем график функции
,
получаем график функции
![]() .
.
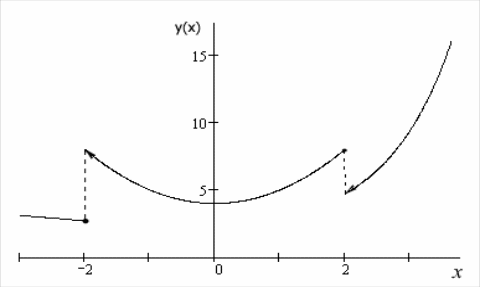
Заметим, что
значение функции
![]() .
Тогда значение функции
.
Тогда значение функции
![]() На графике это отмечено точкой. А теперь,
после проведённых рассуждений построим
график исходной функции.
На графике это отмечено точкой. А теперь,
после проведённых рассуждений построим
график исходной функции.
III. Записать функцию как функцию:
аргумента , полагая
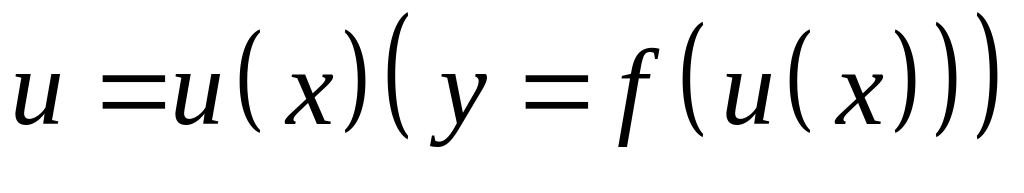 ;
;аргумента
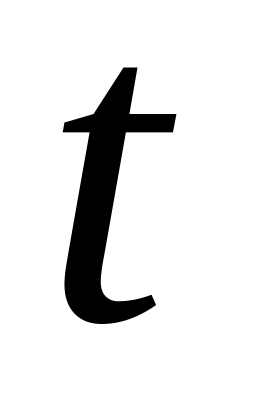 ,
полагая
,
полагая
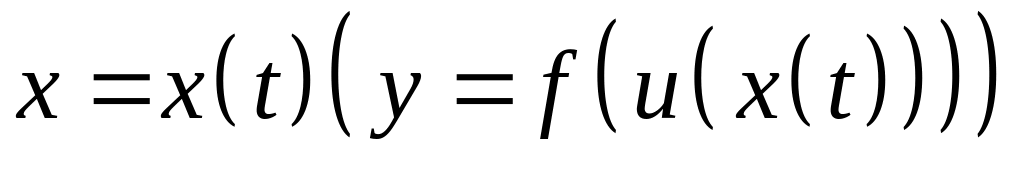 ;
;найти композиции
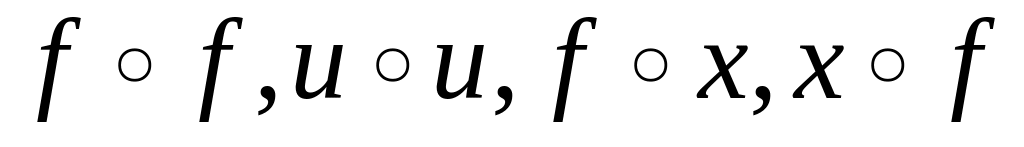 ,
указать внутренние и внешние функции
и схемы вычисления сложных функций.
,
указать внутренние и внешние функции
и схемы вычисления сложных функций.
1.
![]()
Решение.
Полагая , - независимая переменная. Функция
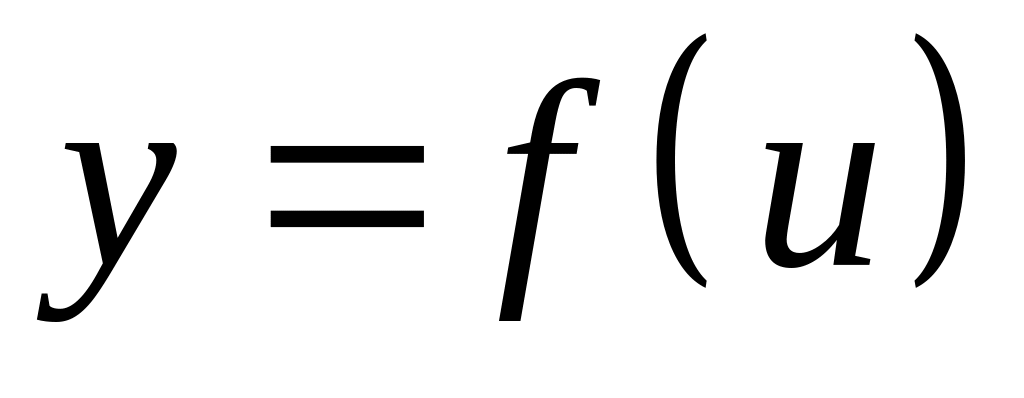 будет иметь вид
будет иметь вид
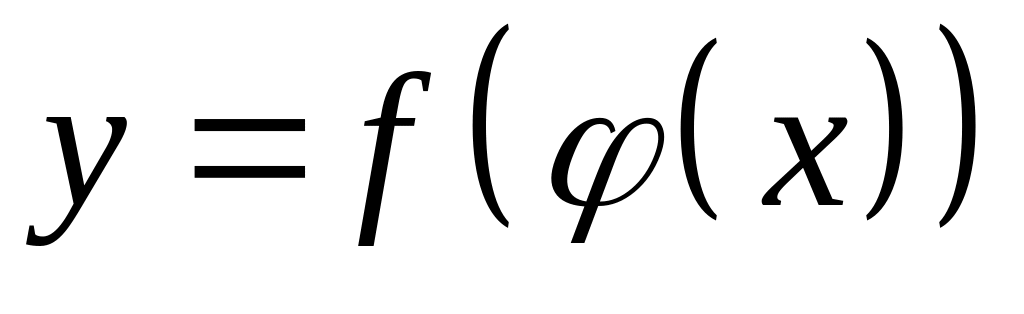 .
Тогда
.
Тогда
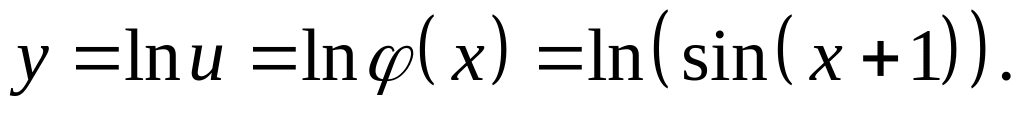
Эта функция вычисляется по следующей схеме:
![]()
Полагая
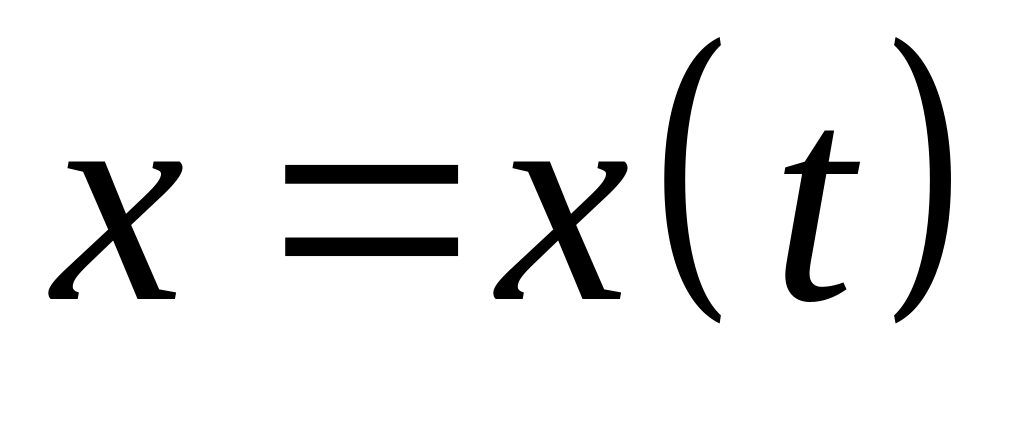 .
считаем
зависимой переменной
.
Функция
будет иметь вид
.
считаем
зависимой переменной
.
Функция
будет иметь вид
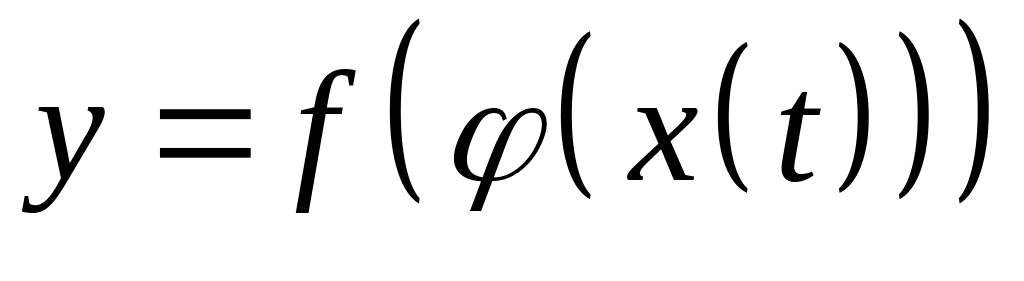 .
Тогда
.
Тогда
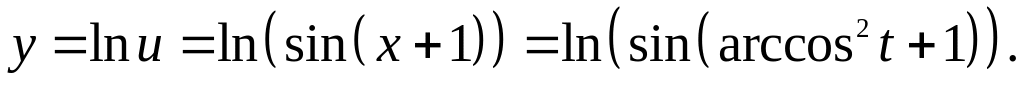
Эта функция вычисляется по следующей схеме
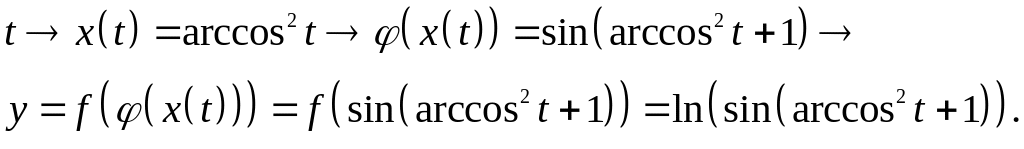
2.
![]()
Решение.
Пусть . В данной функции переменная
 -
зависимая переменная,
-
независимая переменная. Функция
будет иметь вид
.
Тогда
-
зависимая переменная,
-
независимая переменная. Функция
будет иметь вид
.
Тогда
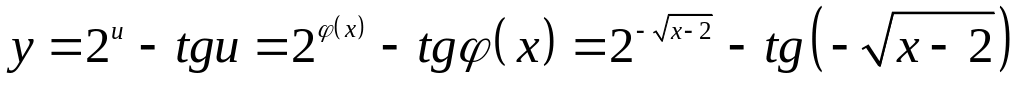 .
.
Эта функция вычисляется по следующей схеме
![]() .
.
Полагая ( считаем зависимой переменной от переменной ). Функция будет иметь вид . Тогда
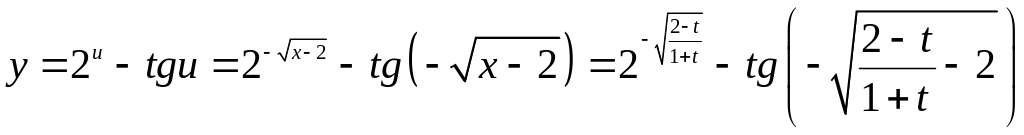 .
.
Эта функция вычисляется по следующей схеме
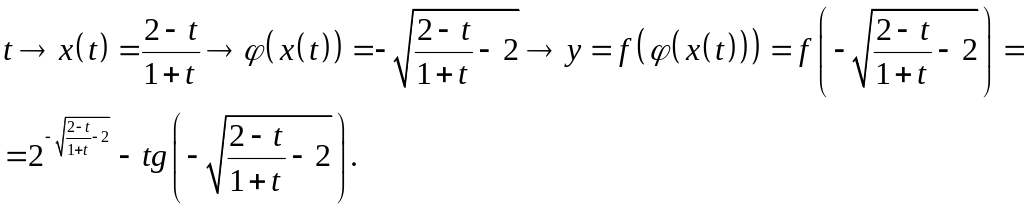
IY. Найти общий вид функции , если она удовлетворяет условию:
1)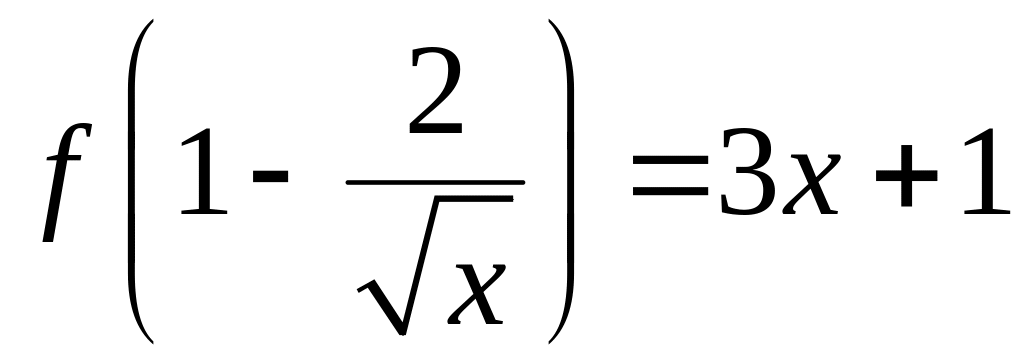 .
.
Решение.
Область определения
функции
![]() .
.
Найдём
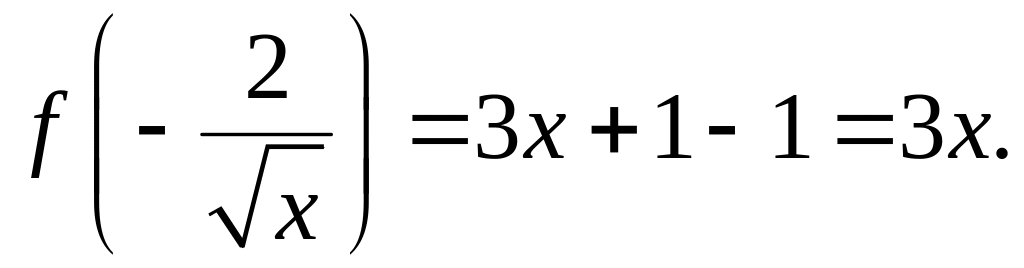 Далее,
Далее,
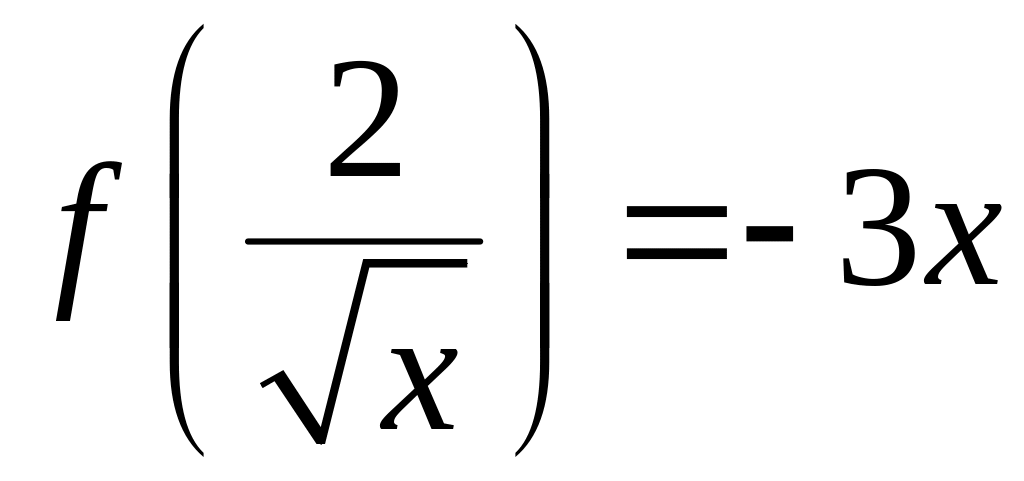 .
Найдём функцию
.
Найдём функцию
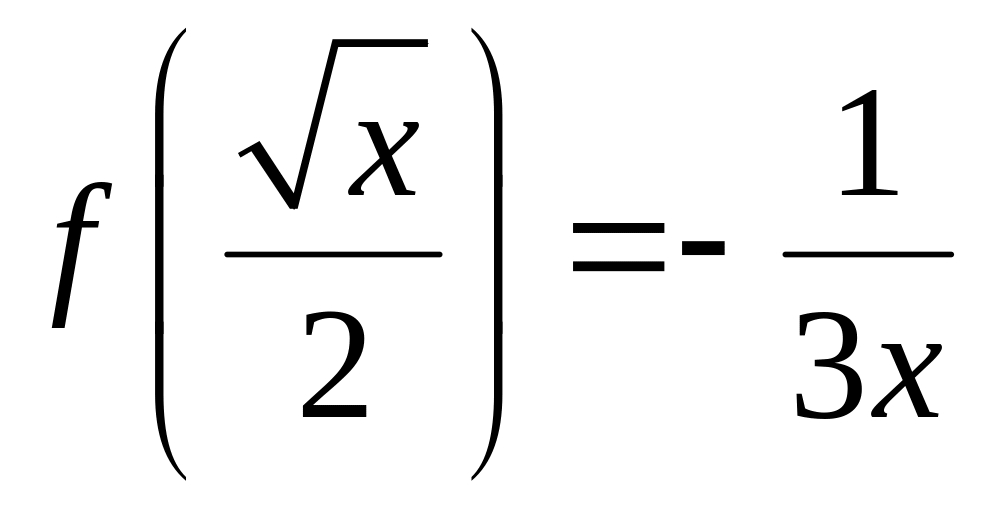 ,
,
![]() и, наконец, найдём общий вид функции
и, наконец, найдём общий вид функции
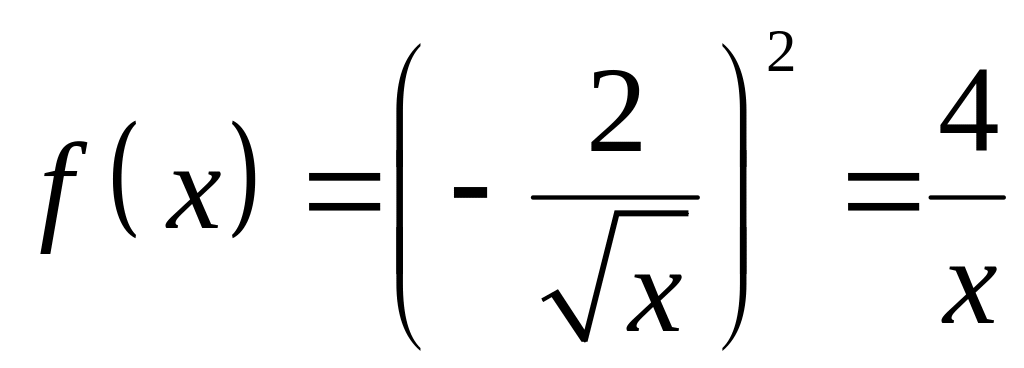 .
.
