СРРиТ / электромагнитные поля и волны
.pdfЗадача 1
Плоская однородная электромагнитная волна распространяется в безграничной полупроводящей среде вдоль оси z. Известны амплитуда напряженности электрического поля Em, частота источника поля f, удельная проводимость среды σ,
ее относительная диэлектрическая проницаемость ε и абсолютная магнитная проницаемость μа=μ0.
Дано: |
|
Em = 50 |
В/м, |
f = 200 |
МГц, |
σ = 2 См/м,
ε = 75.
Необходимо:
1.Определить коэффициент фазы b и коэффициент затухания a распространяющейся волны.
2.Найти модуль |Z| и фазу j комплексного волнового сопротивления среды Z.
3.Записать выражения для комплексных амплитуд и мгновенных значений напряженности электрического и магнитного полей.
4.Определить расстояние z0, на котором амплитуда волны убывает в 1000 раз.
5.Вычислить значения фазовой скорости волны.
6.Найти длину волны в данной среде.
Решение
1. Абсолютная диэлектрическая проницаемость среды распространения волны εа определяется по формуле [2] 1.6
εa = εε0 ,
где e0 = 10−9 Ф - электрическая постоянная. 36p м
Абсолютная магнитная проницаемость среды распространения волны μа определяется по формуле [2] 1.18
μa = μμ0 ,
где m0 |
= 4p×10 |
−7 Гн |
– абсолютная магнитная проницаемость вакуума. |
|
|
м |
|
Тангенс угла диэлектрических потерь определяется по формуле [1] 2.12
tg d = |
s |
|
s |
s |
|
|
|
s |
|
18s ×10−9 |
= |
18·2·109 |
=2.4 . |
||||||
|
= |
|
= |
|
|
= |
|
|
|
= |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
200·106·75 |
|||||||
weа |
2pfee0 |
10−9 |
|
|
10−9 |
fe |
|||||||||||||
|
|
|
|
|
2pfe × |
|
|
|
fe× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36p |
18 |
|
|
|
|
|
|
|
|
|||||
Угол диэлектрических потерь определим по формуле |
|
|
|
||||||||||||||||
δ = arctg(tg(δ)) = arctg (2.4 ) = 1.176 |
(рад). |
|
|
|
|
|
|||||||||||||
Коэффициент фазы волны равен ( [2] 6.7) |
|
|
|
|
|
|
|||||||||||||
b = w
eа2mа × (
1+ (tg d)2 +1)= 2pf 
ee20mа × (
1+ (tg d)2 +1)=
|
|
|
|
|
|
e× |
10 |
−9 |
× 4p×10−7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
36p |
|
|
|
|
|
|
|
|
−8 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||
= 2pf |
|
|
|
|
|
|
× ( |
1+ (tg d) +1)= |
|
|
pf |
×10 |
|
e( |
1+ (tg d) +1)= |
||||||||||||
|
|
|
|
2 |
|
3 |
|
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
|
|
p·200·106·10-8· |
75·( |
|
|
+1) |
= 48.67 |
(м-1). |
|
|
|
|
||||||||||||||
|
|
1+2.4 2 |
|
|
|
|
|
||||||||||||||||||||
3 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Коэффициент затухания распространяющейся волны определим по формуле
[2] 6.8:
a = w
eа2mа × (
1+ (tg d)2 -1)= 2pf 
ee20mа × (
1+ (tg d)2 -1)=
|
|
|
|
|
|
|
|
e× |
10−9 |
|
× 4p×10−7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
36p |
|
|
|
|
|
|
|
|
|
|
|
|
|
−8 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||||||
= 2pf |
|
|
|
|
|
|
|
|
|
|
× ( |
1+ (tg d) -1)= |
|
pf |
×10 |
|
e( 1+ (tg d) -1)= |
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
|
p·200·106·10-8· |
75·( |
|
|
|
|
|
–1) |
= 32.45 |
(м-1). |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1+2.4 2 |
|
|
|
|
|
||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. У волны, распространяющейся в среде с потерями, Zс - комплексная величина |
||||||||||||||||||||||||||||||||||||
([2], 6.11): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Z |
|
= |
|
|
ma |
|
= |
|
|
ma |
|
|
= |
|
Z |
|
×ejϕ , |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
C |
|
|
|
ea (1- jtgd) |
C |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ea |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
|
|
|
| ZC | - модуль комплексного волнового сопротивления; |
||||||||||||||||||||||||||||||||
φ – фаза комплексного волнового сопротивления, которые можно определить по формулам [2] 6.12:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZC |
|
|
= |
|
mа |
×cosd |
= 120p |
m |
× cosd = 120π· |
1 |
·cos(1.176) = 27.0 (Ом), |
|||||
|
|
||||||||||||||||
|
|
|
|
75 |
|||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
eа |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
j = |
1 |
× d = |
1 ×1.176 = 0.588 |
(рад). |
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3. Поле плоской волны, распространяющейся в полупроводящей среде вдоль оси Z, |
|||||||||||||||||
описывается выражением [1] 3.11(комплексная форма): |
|||||||||||||||||
|
∙ |
|
|
|
×e−(α+ jβ)z = 50·е– (32.45+j48.67)z |
æ |
Вö |
|
|
|
|||||||
|
E(z) = Em |
ç |
|
÷, |
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
м ø |
|
|
|
|
∙ |
Em |
|
−(α+ jβ)z− jϕ |
|
50 |
|
–(32.45+j48.67)z–j0.588 |
|
–(32.45+j48.67)z–j0.588 |
æ |
А ö |
||||
|
|
|
|
|
|
||||||||||
H(z) = |
|
|
× e |
|
= |
27.0 |
·е |
|
=1.9·е |
|
|
ç |
|
÷. |
|
|
ZC |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
è |
м ø |
||||
|
|
|
|
|
|
|
|
|
→ → |
|
|
|
|
|
|
Переходя к мгновенным значениям векторов E и H , получаем: |
|
|
|
|
|
||||||||||
E(z) = Em ×e−αz ×cos(wt -bz) =50·е–32.45z·cos(2π·200·106t –48.67z) |
æ |
Вö |
|
|
|||||||||||
ç |
|
÷, |
|
|
|||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
è |
м ø |
|
|
|
|
|
|
Em |
|
|
|
−αz |
|
|
|
|
|
|
|
|
50 |
|
–32.45z |
6 |
|
|||||
H(z) = |
|
|
|
|
|
|
× e |
|
× cos(wt - bz - j) = |
|
27.0 |
·е |
|
|
· cos(2π·200·10 |
|
t –48.67z–0.588)= |
||||||||
|
ZC |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
–32.45z |
|
|
|
6 |
|
|
|
|
|
|
|
|
æ |
А ö |
|
|
||||||||
=1.9·е |
|
|
|
|
|
|
· cos(2π·200·10 |
|
t –48.67z–0.588) |
ç |
|
÷. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
м ø |
|
|
|
4. Зависимость амплитуды поля от расстояния имеет вид |
|
|
|||||||||||||||||||||||
A(z) = Am × e−αz = Am |
е–32.45z. |
|
|
|
|
= ln(Am |
× e−αz0 ). |
|
|
||||||||||||||||
|
|
A |
m |
|
|
|
|
|
×e−αz0 |
|
|
æ |
A |
ö |
|
|
|||||||||
Тогда |
|
|
|
|
|
= Am |
или lnç |
|
m |
÷ |
|
|
|||||||||||||
|
|
n |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
n ø |
|
|
|
|
|
|
|
|
||||||
ln(Am ) − ln(n) = ln(Am ) − αz0 .
Отсюда ln(n) = αz0 .
Расстояние, на котором амплитуда уменьшится в n=1000 раз, равно:
z0 |
= ln(n) |
= ln(1000) |
= |
6.908 |
= 0.2129 (м) = 212.9 (мм). |
|
a |
32.45 |
|
32.45 |
|
5. Фазовая скорость волны определяется по формуле [2] 6.12:
|
w |
|
2pf |
|
2π·200·106 |
|
6 |
æ |
м ö |
|
Vф = |
b |
= |
b |
= |
48.67 |
= 25.82×10 |
|
ç |
|
÷ . |
|
|
|||||||||
|
|
|
|
|
è |
с ø |
||||
6. Длина волны, распространяющейся в полупроводящей среде, равна (формула
[2]6.17):
l = |
2p |
= |
2π |
= 0.1291 (м) = 129.1 (мм). |
|
b |
48.67 |
|
|||
Задача 2
В волноводе радиусом R требуется:
1.Определить критическую и выбрать рабочую длину волны в волноводе.
2.Изобразить распределение электрических и магнитных силовых линий вдоль соответствующих сторон волновода заданного типа волны. Нарисовать эскиз, иллюстрирующий распределение токов проводимости и токов смещения.
3.Изобразить на рисунке с распределением токов проводимости продольные и поперечные излучающие щели.
4.Рассчитать передаваемую мощность, если амплитуда электрической составляющей поля в пучности равна 1 В/м, а также предельно допустимую
мощность (Eпроб = 3×106 В/ м).
5. Определить типы волн, которые могут при выбранной длине волны распространяться в данном волноводе.
Дано:
R = 0.02 м = 20 мм,
Тип волны Н10.
Решение
1. Для данного типа волны критическая длина волны равна (формула [1] 9.50):
2πR
lкр = μmn ,
где μmn – n-й по счету корень первой производной функции Бесселя первого рода порядка m.
Волна заданного типа Н10 не распространяется в волноводе, поэтому выберем волну
типа Н01.
Из таблицы [1] 9.2 следует, что μ01 = 3.832. Тогда
2πR 2π·20
lкр = μmn = 3.832 = 32.793 (мм).
При длине волны λ>λкр электромагнитное поле типа Н01 не распространяется в заданном волноводе.
На рабочей длине волны предположительно должна распространяться волна заданного типа и не должны распространяться волны высших типов.
Найдём критические длины волн ближайших высших типов волн Е:
для волны Е01 λкр= 52.251 (мм), для волны Е02 λкр= 22.765 (мм), для волны Е03 λкр= 14.521 (мм),
для волны Е11 λкр= 32.793 (мм), для волны Е12 λкр= 17.911 (мм), для волны Е13 λкр= 11.729 (мм),
для волны Е21 λкр= 24.472 (мм), для волны Е22 λкр= 14.930 (мм), для волны Е23 λкр= 10.814 (мм).
Найдём критические длины волн ближайших высших типов волн Н:
для волны Н01 λкр= 32.793 (мм), для волны Н02 λкр= 17.911 (мм), для волны Н03 λкр= 12.351 (мм),
для волны Н11 λкр= 68.258 (мм), для волны Н12 λкр= 23.555 (мм), для волны Н13 λкр= 14.722 (мм),
для волны Н21 λкр= 41.174 (мм), для волны Н22 λкр= 18.742 (мм), для волны Н23 λкр= 12.611 (мм),
для волны Н31 λкр= 29.913 (мм), для волны Н32 λкр= 15.679 (мм), для волны Н33 λкр= 11.081 (мм).
Отсюда рабочая длина волны лежит в пределах от 32.793 мм до 29.913 мм. Выберем λраб=30 мм.
2. Для волны типа Нmn индекс m определяет число стоячих волн поля, укладывающихся вдоль окружности волновода, а n – число «полуволн» поля, укладывающихся вдоль радиуса волновода.
Распределение электрических и магнитных силовых линий вдоль соответствующих сторон волновода для волны типа Н01 представлено на рисунке 1.
Н
Е
Рисунок 1 – Силовые линии волны типа Н01 в круглом волноводе
Токи смещения и проводимости в волноводе для поля волны Н01 представлены на рисунке 2.
щели
токи смещения
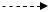токи проводимости
Рисунок 2 – Токи смещения и проводимости для поля волны Н01 внутри волновода
3.Возбуждение излучающей щели осуществляется размещением ее на поверхности, обтекаемой током, т.е. щель должна прерывать ток проводимости на стенке волновода. На рисунке 2 укажем возможные расположения излучающих щелей.
4.Для расчета мощности воспользуемся формулой ([5], стр. 101)
|
pR2E2 |
|
æ |
|
l |
ö2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
P = |
|
|
|
1- ç |
|
|
÷ |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1.57 |
|
ç |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
è lкр ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где R = 2.0 см, Е = |
10-5 кВ/см. Тогда |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
pR2E2 |
|
æ |
|
l |
ö2 |
|
π·22·(10-5)2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
æ |
30 |
ö2 |
|
|
|
|
|
||||||||||||||
P = |
|
|
|
1- ç |
|
|
÷ |
|
= |
|
1.57 |
1 – ç |
|
|
÷ |
= 323.2·10-12 |
(кВт) = |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1.57 |
|
ç |
|
|
÷ |
|
|
|
è32.793ø |
|
|
|
|
|
|||||||||
|
|
|
|
è lкр ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= 323.2·10-9 |
|
(Вт). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
По этой же формуле рассчитаем предельно допустимую мощность |
||||||||||||||||||||||||
|
|
pR2E2 |
|
|
æ |
|
l |
ö2 |
|
π·22·302 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
æ |
30 |
ö2 |
|
|
||||||||||||
P = |
|
|
проб |
1 - ç |
|
|
÷ |
= |
1.57 |
|
1 – ç |
|
|
|
÷ |
|
= 2909.2 |
(кВт) = |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
пред |
|
1.57 |
|
|
|
ç |
|
|
÷ |
|
|
|
è32.793ø |
|
|
|
||||||||
|
|
|
|
è lкр ø |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= 2.91 (МВт).
5. Как указывалось в п. 2, при длине волны λ>λкр электромагнитное поле типа Н01 не распространяется в заданном волноводе. Поэтому на выбранной длине волны λраб=30 мм в заданном волноводе распространяется волны типа Н01, а также волны низших типов, для которых выполняется λкр>λраб, т.е. Е01, Е11,Н11 и Н21.
Задача 3
Необходимо согласовать коаксиальную или двухпроводную линию с заданным значением Zв с активной нагрузкой Rн=qZв в полосе частот от fн до fв.
Модуль коэффициента отражения |Г| на входе перехода Г £ Гдоп . Согласование
произвести ступенчатым переходом с максимально плоской характеристикой. Исходные данные:
Zв=250 Ом, ε=1.
Тип линии – двухпроводная. Радиус проводника a=2.5 мм, fн=45 МГц, fв=130 МГц. q=0.5, |Гдоп|=0.08.
1.Определить количество ступеней перехода N и его общую длину.
2.Найти коэффициенты отражения от ступеней перехода.
3.Волновые сопротивления Zв и геометрические размеры каждой ступени (диаметр внутреннего проводника аi у коаксиала или расстояние между осями проводников 2di в двухпроводной линии).
4. Рассчитать и построить частотную зависимость в полосе частот от 0.8fн до 1.2fв при числе точек не менее 20.
Решение
1) Определить количество ступеней перехода N и его общую длину. Перепад волнового сопротивления равен:
R = |
|
Zв |
= |
|
|
Zв |
= |
|
1 |
|
= 2. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|||||||||||
|
|
|
Rн |
|
|
|
|
|
qZв |
|
|
|||||||||||||
Найдём минимальную, максимальную и среднюю длины волн согласуемого |
||||||||||||||||||||||||
диапазона частот: |
8 |
|
|
|
||||||||||||||||||||
lн |
= |
|
|
с |
= |
|
3×10 |
|
|
= 6.67 |
(м), |
|||||||||||||
|
f |
н |
4.5×107 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
l |
|
= |
|
с |
|
= |
|
3×108 |
|
= 2.31 |
(м), |
|||||||||||||
в |
|
fв |
1.3×108 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
l0 |
= |
|
с |
= |
|
|
|
|
2с |
|
|
= 3.43 |
(м). |
|||||||||||
|
|
|
|
|
(fн + f |
в ) |
||||||||||||||||||
|
|
|
|
|
|
f0 |
|
|
|
|
|
|||||||||||||
Длина ступеньки равна: |
|
|||||||||||||||||||||||
l = |
1 |
|
× |
lн ×lв |
= 0.857 (м). |
|||||||||||||||||||
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
lн + lв |
|
|
|
|
|||||||||||||||
Максимальное рабочее затухание на границе рабочей полосы частот |
||||||||||||||||||||||||
определим по формуле [3] VI.26: |
||||||||||||||||||||||||
Lдоп = |
|
|
|
|
|
1 |
|
|
|
|
|
=1.003. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1- |
|
Гдоп |
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Найдём коэффициент С1 (формула [3] VI.28):
C1 = 2
R((Lдоп)-1) = 0.16 .
R -1
Количество ступеней перехода с максимально плоской АЧХ коэффициента отражения равно (формула [3] 12.29):
lg C1 |
) = 4.953, |
N = lg (cosqн |
где qн = p × lо = 0.808. 2 lн
Выберем количество ступеней перехода равно : N=5.
При этом cos qн = N
С1 = N
0.16 = 0.693, отсюда qн=0.804.
Окончательное значение длины ступеньки равно l = lн ×qн = 0.854 (м). 2p
Общая длина перехода равна : l0 = N ×l = 4.268 (м).
2) Найти коэффициенты отражения от ступеней перехода.
Для числа ступеней N=5÷8 составлены таблицы для точного расчёта звеньев согласующей цепи. Из таблицы [4] 6.05.1 для перепада сопротивления R=2.0 найдём приведённые (к сопротивлению подводящей линии) волновые сопротивления первых двух ступеней:
Z1 = 1.02201;
Z2 = 1.13908.
Приведённые волновые сопротивления остальных ступеней найдём по общей формуле:
Zi × ZN+1−i = R,
откуда
Z3 = 
R = 1.414;
Z4 = R = 1.756, Z2
Z5 = R = 1.957. Z1
Найдём теперь абсолютные волновые сопротивления:
R1 |
= |
Zв |
= 244.6 |
(Ом); |
R 2 |
= |
|
Zв |
= 219.5 |
(Ом); |
|||
Z1 |
Z2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
R3 |
= |
Zв |
|
= 176.8 |
(Ом); |
R 4 |
= |
|
Zв |
|
= 142.4 |
(Ом); |
|
Z3 |
|
|
Z4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
R5 |
= |
Zв |
|
= 127.8 |
(Ом). |
|
|
|
|
|
|
|
|
Z5 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Полученные значения запишем в таблицу 2. |
|
|
|
|
|
|
||||||
Волновое сопротивление двухпроводной линии можно рассчитать по формуле: |
||||||||||||
|
|
|
|
mr |
é |
|
æ d ö |
2 |
ù |
|
||
|
|
Zл(d) := 120 |
×lnê d + |
|
- 1ú |
|
||||||
|
|
|
|
e |
ë |
a |
è |
a |
ø |
|
û, |
|
|
|
|
|
r |
|
|
|
|
||||
где d – полурасстояние между проводами; |
|
|
|
|
|
|
||||||
а – радиус провода. |
|
|
|
|
|
|
|
|
|
|
||
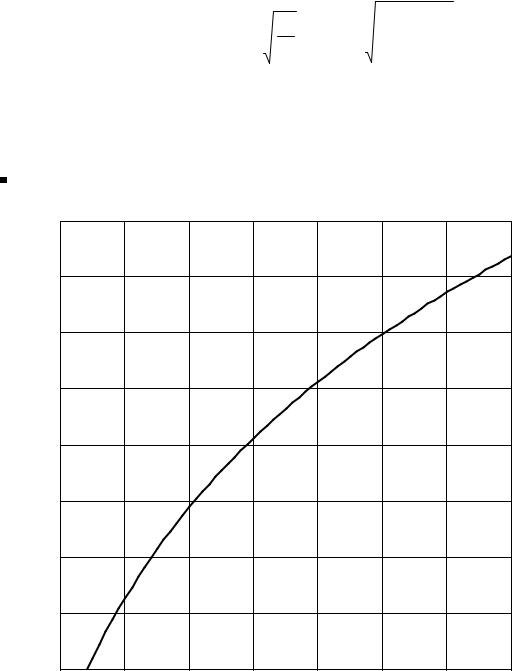
На рисунке 3 приведён график зависимости волнового сопротивления |
||||||||||||
двухпроводной линии для радиуса проводника a=2.5 мм. |
|
|
||||||||||
Zл, Ом |
|
|
|
|
|
|
|
|
|
|
|
|
260 |
|
|
|
|
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
|
|
|
|
|
|
|
220 |
|
|
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
100 3 |
4 |
5 |
6 |
|
7 |
|
8 |
|
|
|
9 |
d, мм |
|
|
|
|
|
10 |
|||||||
Рисунок 3 – Зависимость волнового сопротивления двухпроводной линии от |
||||||||||||
|
полурасстояния между проводниками (при а=2.5 мм) |
|||||||||||
По рисунку 3 определим полурасстояния между проводниками для полученных волновых сопротивлений ступеней.
Линия Zв : d0 = 10.19 (мм)
Ступень |
R1 : |
d1 |
= 9.76 |
(мм) |
Ступень |
R2 : |
d2 |
= 7.98 |
(мм) |