
СРРиТ / 6 вариант
.docx2.1 Общая характеристика контрольного задания
Рассматривается система передачи ТВ сигналов с двухполосной амплитудной модуляцией (рисунок 1).

Рисунок 1 − Структурная схема системы передачи ТВ сигналов
Структурная схема системы содержит ФНЧ 1, двухполосный амплитудный модулятор 2, генератор 3 несущей частоты f0, широкополосный усилитель 4 высокой частоты (на передающей стороне), линию связи 5, ПФ 6, широкополосный усилитель 7 высокой частоты, амплитудный демодулятор 8, ФНЧ 9 (на приемной стороне).
 ,
,
 − число букв в фамилии студента;
− число букв в фамилии студента;
 ,
,
 − число букв в имени студента;
− число букв в имени студента;
 ,
,
 − число букв в отчестве студента;
− число букв в отчестве студента;
 ,
,
 ,
,
 − коэффициенты, представляющие число
− коэффициенты, представляющие число

 в
в
 -разрядной
двоичной системе исчисления.
-разрядной
двоичной системе исчисления.
Определим исходные данные для выбора значений для расчета.

На основании
значения
 выбираем исходные значения для
моделирования в соответствии с таблицей
2.1 [1].
выбираем исходные значения для
моделирования в соответствии с таблицей
2.1 [1].
Таблица 2 – Исходные значения для моделирования
|
Параметр |
aD10, дБ |
aS10, дБ |
aD60, дБ |
aS60, дБ |
aD90, дБ |
aS90, дБ |
f0, МГЦ |
t1Н |
t2Н |
t3Н |
t4Н |
|
Значение |
1.30 |
30 |
0.20 |
22 |
0.30 |
26 |
70 |
0 |
6 |
6 |
6 |
аD1 (аD6, аD9) — допустимая неравномерность характеристики рабочего затухания ФНЧ 1 (ПФ 6, ФНЧ 9) в полосе пропускания;
аS1 (аS6, аS9) — минимальное рабочее затухание ФНЧ 1 (ПФ 6, ФНЧ 9) в полосе .задерживания;
 − нормированные
(к частоте k)
моменты времени;
− нормированные
(к частоте k)
моменты времени;
f0 — несущая частота исследуемой системы передачи.
1.1. Построим
операторную передаточную функцию K1(p)
ФНЧ 1, используя метод рабочих параметров
и выбирая ХРЗ модели Золотарева-Кауэра
(идентификационный коэффициент
 =0).
=0).
Для этого первоначально необходимо рассчитать значения:
FD1 — граничной частоты полосы пропускания ФНЧ 1;
FS1 — граничной частоты полосы задерживания ФНЧ 1,
 -
нормированная частота,
-
нормированная частота,
В соответствии с формулами:
FD1=(1+0.1∙ )
FD10
(FD10=3·106
Гц) (1.1.1)
)
FD10
(FD10=3·106
Гц) (1.1.1)
FS1=(1+0.1∙ )
FS10
(FS10=6·106
Гц) (1.1.2)
)
FS10
(FS10=6·106
Гц) (1.1.2)
 (1.1.3)
(1.1.3)

На основании
полученных и исходных данных ( )
по справочнику [2] выбираем требуемый
вид ХРЗ, находим операторную передаточную
функцию и выписываем требуемые
коэффициенты. Выбираем ФНЧ-прототип
С0350.
)
по справочнику [2] выбираем требуемый
вид ХРЗ, находим операторную передаточную
функцию и выписываем требуемые
коэффициенты. Выбираем ФНЧ-прототип
С0350.
ФНЧ-прототип С0350 имеет следующую передаточную функцию:
 (1.1.4)
(1.1.4)
Таблица 1.1 – Параметры выбранного ФНЧ-прототипа С0350
|
Параметры |
Значения параметров |
|
aD1, дБ |
1.2494 |
|
aS1, дБ |
29,7 |
|
|
1,869159100 |
|
|
0,8889773703 |
|
|
0,5177459569 |
|
|
0,1860421946 |
|
|
0,9749582817 |
|
|
6,481381562 |
2.1. В диапазоне реальных частот (0 − 3FD1) построить на ПЭВМ АЧХ, ФЧХ и ХРЗ ФНЧ 1.
Операторную передаточную функцию можно записать в показательной форме:

Соответственно
АЧХ ФНЧ1 представляет собой модуль от
операторной передаточной функции
 ,
ФЧХ – аргумент, ХРЗ находим в соответствии
с тем, что она является обратной АЧХ.
,
ФЧХ – аргумент, ХРЗ находим в соответствии
с тем, что она является обратной АЧХ.
 ,
дБ
,
дБ
Определим

Построим в среде MathCad АЧХ, ФЧХ и ХРЗ ФНЧ1 в диапазоне частот (0-9,9) МГц, а также нормированные характеристики.
При этом необходимо
произвести денормирование коэффициентов
математической модели прототипа ФНЧ1
С0350 путем замены
 .
.


Рисунок 2.1.1 – Нормированная и денормированная АЧХ ФНЧ1


Рисунок 2.1.2 – Нормированная и денормированная ХРЗ ФНЧ1


Рисунок 2.1.3 – Нормированная и денормированная ФЧХ ФНЧ1
1.2.
Построить операторную передаточную
функцию K6(p)
ПФ 6, используя метод рабочих параметров
и выбирая ХРЗ модели Золотарева-Кауэра
( =0).
=0).
Рассчитаем:
F+D6 (F-D6) - верхняя (нижняя) граничная частота полосы пропускания ПФ 6;
F+S6 (F-S6) - верхняя (нижняя) граничная частота полосы задерживания ПФ 6;
F+D6=f0+(1+ )FD10;
(1.2.1)
)FD10;
(1.2.1)
F-D6=
f0−(1+ )FD10; (1.2.2)
)FD10; (1.2.2)
F+S6=
f0+(1+ )FS10; (1.2.3)
)FS10; (1.2.3)
F-S6=
f0−(1+ )FS10 (1.2.4)
)FS10 (1.2.4)

Проверим удовлетворяют ли полученные частоты условию геометрической симметрии:



Соответственно условие симметрии не соблюдается. Выполним процедуру симметрирования исходной ХРЗ:
- выбираем и
фиксируем частоты
 ,
,
 ,
,
 ;
;
- из условия геометрической симметрии находим частоту


Проверим выполнение условия:

 - условие выполняется.
- условие выполняется.
Вычислим частоту гарантированного затухания ФНЧ-прототипа:
 (1.2.5)
(1.2.5)

И постоянную преобразования:
 (1.2.6)
(1.2.6)

По справочнику [2] выбираем ФНЧ-прототип С0320 с соотвествующими параметрами:
Таблица 1.2 – Параметры выбранного ФНЧ-прототипа С0320
|
Параметры |
Значения параметров |
|
aD1, дБ |
0.1773 |
|
aS1, дБ |
25,6 |
|
|
2,201216296 |
|
|
0,9597323337 |
|
|
0,3384707723 |
|
|
1,459273151 |
|
|
3,536183067 |
Выполняем процедуру преобразования модели ФНЧ-прототипа в модель проектируемого ПФ. Для этого произведем замену:
 (1.2.7)
(1.2.7)
Тогда операторная передаточная функция будет выглядеть следующим образом:

2.1 В диапазоне реальных частот от (f0−3F-D6) до (f0+3F+D6) построить АЧХ, ФЧХ и ХРЗ ПФ 6.
При этом необходимо
произвести денормирование коэффициентов
математической модели прототипа ФНЧ
С0320 путем замены
 .
.

Соответственно, диапазон частот для построения характеристик от (-131,06 – 288,94) МГц.


Рисунок 2.2.1 – Нормированная и денормированная АЧХ ПФ6


Рисунок 2.2.2 – Нормированная и денормированная ХРЗ ПФ6


Рисунок 2.2.3 – Нормированная и денормированная ФЧХ ПФ6
1.3. Построим
операторную передаточную функцию K9(p)
ФНЧ 9, используя метод рабочих параметров
и выбирая ХРЗ модели Золоторева-Кауэра
(идентификационный коэффициент
 =0).
=0).
Для этого первоначально необходимо рассчитать значения:
FD1 — граничной частоты полосы пропускания ФНЧ 1;
FS1 — граничной частоты полосы задерживания ФНЧ 1,
 -
нормированная частота,
-
нормированная частота,
В соответствии с формулами:
FD9=(1+0.1∙ )/
FD90
(FD90=6·106
Гц) (1.3.1)
)/
FD90
(FD90=6·106
Гц) (1.3.1)
FS9=(1+0.1∙ )/
FS90
(FS90=12·106
Гц) (1.3.2)
)/
FS90
(FS90=12·106
Гц) (1.3.2)
 (1.3.3)
(1.3.3)

На основании
полученных и исходных данных ( )
по справочнику [2] выбираем требуемый
вид ХРЗ, находим операторную передаточную
функцию и выписываем требуемые
коэффициенты.
)
по справочнику [2] выбираем требуемый
вид ХРЗ, находим операторную передаточную
функцию и выписываем требуемые
коэффициенты.
ФНЧ-прототип С0325 имеет следующую передаточную функцию:

Таблица 1.3 – Параметры выбранного ФНЧ-прототипа С0325
|
Параметры |
Значения параметров |
|
aD1, дБ |
0.2803 |
|
aS1, дБ |
28,6 |
|
|
2,270068086 |
|
|
0,8312472565 |
|
|
0,3112809126 |
|
|
1,0939937610 |
|
|
4,791901348 |
3. В диапазоне реальных частот (0 − 3FD9) построить АЧХ, ФЧХ и ХРЗ ФНЧ 9.
FD9=
FD90
/ (1+0.1∙ )
= 6·106/
(1+0.3) = 4,62 МГц
)
= 6·106/
(1+0.3) = 4,62 МГц
Построим характеристики в среде MathCad в диапазоне частот (0 – 13,86) МГц


Рисунок 2.3.1 – Нормированные и денормированные АЧХ ФНЧ9


Рисунок 2.3.2 – Нормированная и денормированная ХРЗ ФНЧ9


Рисунок 2.3.3 – Нормированная и денормированная ФЧХ ФНЧ9
3. Проанализировать математическую модель
 (3.1)
(3.1)
входного
измерительного сигнала ( ,
,
 − идентификационные коэффициенты).
Построить на ПЭВМ график зависимости
− идентификационные коэффициенты).
Построить на ПЭВМ график зависимости
 интервале (0, 4t2).
интервале (0, 4t2).
Запишем входное воздействие с учетом заданных значений:

Построим график Uвх(t):

Рисунок 3.1 – Входной сигнал
б)
Вычислим лапласовское изображение
 измерительного сигнала
измерительного сигнала
 :
:

Учтём,
что
 , а также при расчетах cos
x
перепишем по формуле Эйлера:
, а также при расчетах cos
x
перепишем по формуле Эйлера:  .
.

Далее найдем передаточную функцию цепи. Фильтр С0350-6 с частотой среза равной 5МГц, у которого следующие параметры:

Характеристическая функция фильтра:

Преобразуем нормированную комплексную передаточную функцию в денормированную заменой переменной p на p/fD, где fD=5МГц нормирующая частота (граничная частота полосы пропускания ФНЧ):

Вычисление реакции h(t) на периодическое воздействие по модели с использованием ряда Фурье требует больших затрат ресурсов для проведения расчета, с учетом этого целесообразно использовать метод Ильинкова, используя выражения (1.17), (1.20) [1], представляющими реакцию в любой точке периодического интервала конечной суммой, число слагаемых которой определено порядком передаточной функции K(p).





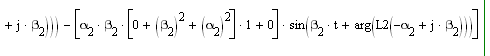





Рисунок 4.2 – Вид нормированной переходной характеристики
звена

Рисунок 4.3 – Вид денормированной переходной характеристики исследуемого звена

Рисунок 4.4 – Вид реакции звена входной сигнал
(денормированный)
ЛИТЕРАТУРА
1 В.А. Ильинков, В.Е. Романов Пособие для самостоятельной работы «Моделирование систем телекоммуникаций», - Мн, БГУИР, 2009 г.
2 Р. Зааль Справочник по расчету фильтров, - М, Радио и связь, 1983 г.
















