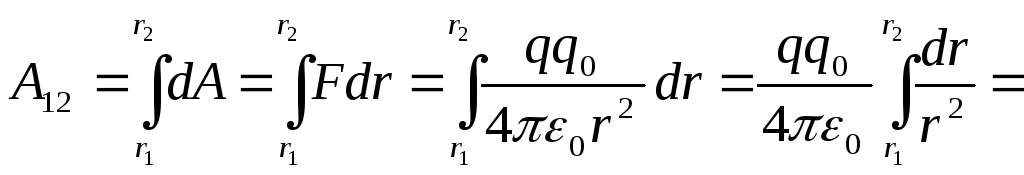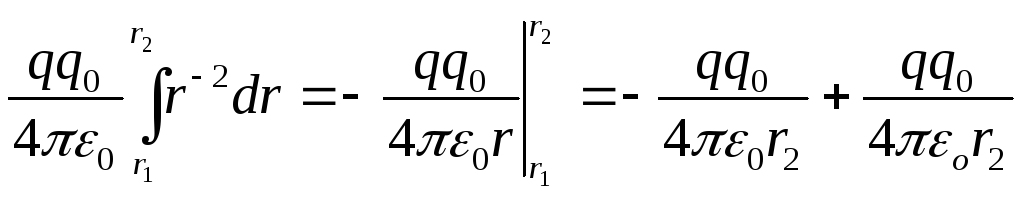шпоры по физике(1)
.doc|
№26. Правила Кирхгофа для разветв. цепей. Непосредственный расчет разветвленных цепей, содержащих неск-ко замкн. контуров осущ-ся с пом. 2 правил Кирхгофа. Первое правило Кирхгофа: алгебр. сумма токов, сходящихся в узле, равна нулю:
Нарп-р, для рис.1 первое правило Кирхгофа запиш-ся так: I1-I2+I3-I4-I5=0 Первое правило Кирхгофа вытеает из з-на сохр-ия электр. заряда. Дейвст-но, в случае установившегося пост. тока ни в одной точке проводника и ни на одном его участке не должны накпал-ся электр. заряды. В противном случае токи не могли бы оставаться постоянными.
В
Складывая почленно
эти уравнения, получим
Это
уравнение выражает второе
правило Кирхгофа:
в любом замкнутом котуре, произвольно
выбранном в разветвленной электр-й
цепи, алгебр. сумма произведений силы
токов Ii
на сопротивление Ri
соответствующих участков этого контура
равна алгебр. сумме э.д.с. εk,
встречающихся в этом котуре:
|
№28. Магнитное поле и его хар-ки. Опыт пок-ет, что, подобно тому, как в простр-ве, окружающем электр. заряды, возникает электростат. поле, так и в простр-ве, окружающем токи и пост. магниты, возн-ет силовое поле, называемое магнитным. Наличие магн. поля обнаруживается по силовому д-вию на внесен. в него проводники с током или пост. магниты. Название «магнитное поле» связывают с ориентацией магн. стрелки под дейст-м поля, создаваемого током. Электр. поле д-вует как на неподвижные, так и на движущиеся в нем электр. заряды. Важнейшая особ-сть магн. поля состоит в том, что оно д-вует только на движущиеся в этом поле электр. заряды. Опыт пок-ет, что хар-р возд-вия магн. поля на ток различен в зав-сти от формы проводника, по кот-му течет ток, от расположения пров-ка и от напр-ния тока. След-но, чтобы охарак-вать магн. поле, надо рассм-ть его д-вие на опр. ток.
П Опыты пок-ют, что магн. поле оказывает на рамку с током ориентирующее д-вие, поворачивая ее опр. образом. Этот результат исполь-ся для выбора напр-ния магн. поля. За напр-ние магн. поля в данной точке приним-ся напр-ние, вдоль кот-го располаг-ся положит. нормаль к рамке. За напр-ние магн. поля м/б также принято напр-ние, совпадающее с напр-нием силы, которая д-вует на северный полюс магн. стрелки, помещенной в данную точку. Так как оба полюса магн. стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. След-но, на магн. стрелку д-вует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с напр-нием поля. Рамкой с током м. воспольз-ся также и для количеств. описания магн. поля. Так как рамка с током испытывает ориентир. д-вие поля, то на нее в магн. поле действует пара сил. Вращ. момент сил зависит как от св-в поля в дан. точке, так и от св-в рамки и опр-ся формулой M=[pmB], где pm — вектор магн. момента рамки с током (В — вектор магн. индукции, количеств. хар-ка магн. поля). Для плоского контура с током I pm=ISn где S— площадь поверхности контура (рамки), n — единичный вектор нормали к поверхности рамки. Напр-ние pm совпадает, таким образом, с напр-нием положит. нормали. Если в данную точку магн. поля помещать рамки с различными магн. моментами, то на них д-вуют разл. вращ. моменты, однако отн-ние Mmax/pm (Мmax – макс. вращающий момент) для всех контуров одно и то же и поэтому м. служить хар-кой магн. поля, называемой магн. индукцией: В=Mmax/pm Магн. индукция в дан. точке однородного магн. поля определяется макс. вращ. моментом, действующим на рамку с магн. моментом, равным единице, когда нормаль к рамке перпенд-на напр-нию поля. Т.к. магн. поле явл-ся силовым, то его, по аналогии с электрическим, изображают с помощью линий магн. индукции — линий, касательные к которым в каждой точке совпадают с напр-нием вектора В. Их напр-ние задается правилом правого винта: головка винта, ввинчиваемого по напр-нию тока, вращается в напр-нии линий магн. индукции. Вектор магн. индукции В м. хар-ет результирующее магн. поле, создаваемое всеми микор- и макротоками, т.е. при одном и том же токе и прочих равных условиях вектор В в разл. средах б. иметь разл. значения. Магн. поле макротоков опис-ся вектором напряженности Н. Для однородн. изотропной среды вектор магн. индукции связан с вектором напр-сти след. отн-нием: B=µ0µH, где µ0- магнитная постоянная, µ-безразмерная величина – магн. проницаемость среды, показывающая во ск-ко раз магн. поле макротоков Н усиливается за счет поля микротоков среды.
|
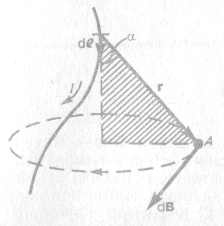
№29. Закон Био-Савара-Лапласа. Закон Ампера. З-н Био-Савара-Лапласа. Рассмотрим проводник с током, выделим в проводнике какой-нибудь элемент dl.
Направление вектора совпадает с напр-ем тока I. Проведем перпендикуляр к точка А.
где
µ0 – магнитная постоянная µ- магнитная проницаемость среды. Определяет индукцию в каждой точке поля. З-н Ампера. Как показывает опыт, на проводник с током, помещенный в магн. поле д-ет сила F.
Франц. физик Ампер
иссл-л разл. случаи д-вия магн. поля на
проводник с током. В рез-те провед.
исслед-й он установил, что сила
где I-
сила тока в проводнике; dl-
элемент проводника;
Как известно,
След-но,
dF=I*dl* B*sinα
Рассм-м, как
опред-ся напр-ие вектора
Допустим
|
|
№30. Явление электромагн. индукции. З-н Фарадея. B-число линий индукции, проходящих ч/з единицу площади S*B=dφ – поток индукции BS- число линий индукции, проходящих ч/з S. При приближении магнита к контуру (рамка) число линий, пересекающих площадь ограниченную рамкой, увел-ся, т.е. усиливается поток индукции. Как пок-ет опыт, только в этом случае возникает электр. ток. Явление возникновения электр. тока в замкн. контуре при изменении потока индукции ч/з S огранич. контура, наз-ся электромагн. индукцией. Т.к. в контуре возникает I(сила тока), возникает и э.д.с. (ЭДС индукции) Из опыта следует, что величина ЭДС индукции (Ei) пропорциональна скорости изменения магн. потока:
где dφ/dt – скорость изменения магн. потока. Это и есть закон Фарадея.
№6.Энергия, работа, мощность. Энергия — универсальная мера разл. форм движения и взаимод-вия. С разл. формами движения материи связывают разл. формы энергии: мех-ую, тепловую, электромагнитную, ядерную и др. В одних явл-х форма движения материи не изменяется (напр-р, горячее тело нагревает холодное), в других — переходит в иную форму (напр-р, в рез-те трения мех. движение превр-тся в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом др. телу, равна энергии, полученной последним телом. Энергией – наз-ся скалярная физ. вел-на, являющаяся единой мерой разл. форм движения материи и мерой перехода движения материи из одних форм в другие. Осн. св-во разл. видов энергии явл-ся их взаимопревращаемость. В более конкретных случаях энергией называется вел-на, характеризующая способность тела, системы, машины совершать работу. Изменение мех. движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно хар-вать пр-с обмена энергией м/у взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует пост. сила F, которая составляет некоторый угол α с напр-нием перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs= Fcosα), умноженной на перемещение точки приложения силы: A= Fs*s=Fscosα (1) В общем случае сила м. изменяться как по модулю, так и по напр-нию, поэтому формулой (1) пользоваться нельзя. Если, однако, рассмотреть элементарн. перемещение dr, то силу F м. считать пост-ной, а движение точки ее приложения — прямолинейным. Элементарной работой силы F на перемещении dr наз-ся скалярная величина: dA=Fdr= Fcosαds= Fsds.
где
α—
угол между векторами F
и dr;
ds=│dr│-
элементарный путь; Fs
— проекция
вектора F
на вектор dr
.
Работа силы на участке траектории от точки 1 до точки 2 равна алгебр-й сумме элементарных работ на отд. бесконечно малых участках пути. Эта сумма приводится к интегралу
Д
где s — пройденный телом путь. Из формулы (1) следует, что при α< п/2 работа силы положительна, в этом случае составляющая Fs, совпадает по напр-нию с вектором скорости движения v. Если α> п/2, то работа силы отриц-на. При α= п/2 (сила напр-на перпендикулярно перемещению) работа силы равна 0. Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м(1 Дж=1 Н м). Чтобы охар-ть ск-сть совершения работы, вводят понятие мощности: N=dA/dt За время dt сила F сов-ет работу Fdr, и мощность, развиваемая этой силой, в данный момент времени N=(Fdr)/dt=Fv т. е. равна скалярному произведению вектора силы на вектор ск-сти, с кот-й движется точка приложения этой силы; N — величина скалярная. Ед-ца мощности - ватт (Вт): 1 Вт — мощность, при кот-й за время 1 с совершается работа 1 Дж (1 Вт=1 Дж/с). |
|
|
|
|
№21. Потенциал электростат. тока.
Т.к. q0 перемещается и совершает работу, след-но, от обладает энерией (потенциалом); U1 – в точке 1, U2 – в точке 2. U1>U2. ΔU=U1-U2 – убыль энергии. За счет ΔU совершается работа А. А=ΔU=U1-U2 (1) Работу А12 можно найти ещё след. образом: dA=F*dr F- сила, приложенная к пробному заряду dr – элементарн. перемещение в напр-нии действия силы.
Из этого следует, что
Отн-ние потенц. энергии пробного заряда к величине этого заряда в какой-то точке поля- потенциал эл. поля. Это отн-ние не зависит от величины q, опр-ся св-вами поля. φ=U/q0 (3) Потенциал хар-ет какой потенц. энергией обладает поле в данной точке. Потенциал φ в какой-либо точке электростат. поля есть физ. вел-на. определяемая потенц. энергией единичного положит. заряда, помещенного в эту точку. Из формул (2) и (3) следут, что потенциал поля, создаваемого точечным зарядом q, равен
Работа, совершаемая силами электростат. поля при перемещении заряда q0 из точки 1 в точку2 . м.б. представлена как: A12=U1-U2=Q0(φ1-φ2) (5) т.е. равна произведению перемещаемого заряда на разность потенциалов в начальн. и конечных точках. Разность потенциалов двух точек 1 и 2 в электростат. поле опр-ся работой, совершаемой силами поля. при перемещении единичного положит. заряда из т. 1 в т. 2. |
|
|
№20.Электростат. поле. Напряженность Эл. Поля. Если в простр-во, окр-щее эл-кий заряд, ввести др. заряд, то на него будет действовать кулоновская сила; зн-т, в простр-ве, окр-щем эл. заряды, сущ-ет силовое поле. В данном сл-е говорят об электрическом поле — поле, посредством к-ого взаимод-ют эл-ие заряды. Мы будем рассм-вать эл-ие поля, к-ые созд-ся неподвижными эл-ими зарядами и наз-ся электростат-ими.
Для обнаружения
и опытного исслед-ия ЭП
исп-ется пробный точечный “+“ заряд
— такой заряд, который не искажает
иссл-ое поле (не вызывает перераспред-ния
зарядов, созд-их поле). Если в
поле,созд-емое зарядом Q
поместить пробный заряд Qо,
то на него действует сила F
различная в разных точках поля, к-ая,
согласно закону Кулона
Напряж-сть ЭП в данной точке есть физ-кая величина, опр-емая силой, действующей на пробный ед-чный положит. заряд, помещенный в эту точку поля. E =F / Q0 (1) Как следует из ф-лу (1) и (2), напряж-ть поля точечного заряда в вакууме
Напр-ние вектора Е совпадает с напр-нем силы, действующей на “+“ заряд. Если поле создается “+“зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного “+“ заряда); если поле создается “-“зарядом, то вектор Е направлен к заряду
(рис. 118).
Из ф-лы (1) следует, что ед-ца напряж-ти ЭП – (Н/Кл): 1 Кл действует с силой в 1 Н; 1 Н/Кл=1 В/ м, где В(вольт)- ед-ца потенциала ЭП.
Чтобы с помощью ЛН можно было хар-ать не только напр-ние , но и знач-ие напряж-ти ЭП, условились проводить их с определенной густотой (см. рис.): число ЛН, пронизывающих ед-цу площади пов-ти, перпендик-ную ЛН, д\б равно модулю вектора Е. Тогда число ЛН, пронизывающих элементарную площадку dS, нормаль n которой образует угол а с вектором Е, равно EdS cos a = EndS, где Еn — проекция вектора Е на нормаль n к площадке dS Величина dФE=EndS=EdS наз-ся потоком ВН через площадку dS. Здесь dS=dSn — вектор, модуль к-ого равен dS, а напр-ние совпадает с напр-нием нормали n к площадке. Выбор напр-ния вектора n (а сл-но, и dS) условен, т. к. его можно направить в любую сторону. Ед-ца потока ВН ЭП —1 В*м. Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверх-ть
где интеграл берется по замкнутой поверх-ти S. Поток вектора Е явл-ся алгебр-кой величиной: зав-т не только от конфигурации поля Е, но и от выбора напр-ния n. Для замкнутых поверх-тей за + направление нормали принимается внешняя нормаль, т. е. нормаль, напр-ная наружу области, охватываемой поверх-тью.
|
№22. Эл. емкость уедин. проводника. Конденсаторы. Рассм-м уединенный пров-к, который удален от других проводников, тел и зарядов. Его потенциал прямо пропорционален заряду проводника. Из опыта следует. что разные проводники, будучи одинаково заряженными. имеют разн. потенциалы. Поэтому для уедин. проводника м. записать: Q=Cφ. Величину C=Q/φ наз-ют электроемкостью уедин. пров-ка. Емкость уедин. пров-ка опр-ся зарядом, сообщение которго проводнику изменяет его потенциал на единицу. Емк-сть пров-ка зависит от его размеров и формы. но не зависит отматериала, агрегатного сотояния, вормы и размеров полостей внуотри проводника. это связано стем, что избыточные заряды распред-ся на внешн. поверх-сти проводника. Емкость также не зависит от заряда проводника и его потенциала. [С]=[q]/[φ]= 1К/1В= 1Ф. 1Ф- это електроемк-сть такого пров-ка, у которого при увеличении потенциала на 1 В, заряд увел-ся на 1К. ЭЛЕКТРОЕМКОСТЬ ШАРА: φ=q/4πε0εr; электроемкость уединенного шара: C=4πε0εr; E= - dφ/dr; dφ= - Edr; ∆φ= - ∫[r1 – r2] Edr; C=q/∆φ; В ∆φ’= - ∫[r1 – r2] E’dr; ∆φ’<∆φ; C’=q/∆φ’; C<C’; Видно, что электроемкость уединенного проводника всегда меньше, чем теплоемкость неуединенного.
Устройства, обладающие сп-тью при малых размерах и небольших отн-но окружающих тел потенциалах накапливать значительные по величине заряды, иными словами обладать большой емкостью, наз-ся конденсаторами. Конденсатор состоит из 2 проводников, разделенных диэлектриком. на емкость конденсатора не д. оказывать влияния окруж. тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узк. зазоре м/у обкладками конденсатора. Этому условию удовлетворяют:1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зав-сти от формы обкладок конд-ры дел-ся на плоские, цилиндрические и сферические. Т.к. поле сосредоточено внутри конденсатора, то линии напр-сти начинаются на одной обкладке и кончаются на другой, поэтому своб. заряды, возникающие на разных обкладках, явл-ся равными по модулю разноименныим зарядами. Под емкостью конденсатора понимается физ. вел-на, равная отн-нию заряда Q. накопленного в конденсаторе, к разности потенциалов (φ1-φ2) м/у его обкладками: C=Q/(φ1-φ2)
|
№24. Электродвижущая сила и напряжение.
Пока сущ-ет
разность потенциалов , происх-т движение
зарядов в эл поле от точек с большим
потенциалом к точкам с меньшим
потенциалом. Но по мере премещ-я зарядов
V1
уменьш-ся,V2
увелич-ся.
В рез-те потенциалы на концах станут
равными, эл поле исчезнет и движ-е
зарядов прекратиться. След-но, чтобы
по проволнику двигался ток, необх-мо
сохранить на концах проводника разность
потенц-лов, т.е. необх-мо все время для
поддержания тока положит-ные заряды
из точки с потенц-лом V2
возвращать в точку с V1,
т.е. перемещать заряды против направления
движ-я эл
поля, кот
будет препятствовать этому перемещ-ю.
поэтому необх-мо исп-ть силы неэлектрич-го
происх-я (сторонние силы). Н-р, в
гальванических эл-тах они возн-ют за
счет энергии химич-ких реакций, в
генераторе – за счет механической
энергии. Чтобы поддерживать разность
потенциалов постоянной исп-ют прибор
– источник тока. При перемещ-и заряда
соверш-ся работа. Физ. величина, равная
работе сторонних сил по перемещ-ю
единицы заряда – ЭДС: ε = A/Q0.
ЭДС выраж-ся в вольтах. Сторонняя сила
Fст
,дейст-щая на заряд Q0,
м.б. выражена: Fст
=ЕстQ0,
где Е- напряженность поля сторонних
сил. Работа сторонних сил по перемещ-ю
заряда на замкнутом участке цепи
равна: А= ∫ Fст
dl
= Q0
∫ Eст
dl.
След-но получим выражение для ЭДС,
действующей в цепи: ε= ∫ Eст
dl,
т.е. ЭДС, действ-щая в замкнутой цепи,
м.б. определена как циркуляция вектора
напряженности поля сторонних сил. На
заряд Q0
действуют также силы электростатического
поля Fe=
Q0E.
Т.о. результирующая сила, действ-щая
на заряд, равна F=
Fст+Fe=
Q0(Eст
+ E).
Работа, совершаемая результир-щей
силой над зарядом на участке 1-2, равна
Напряжением на участке 1-2 наз-ся физ величина, опр-мая работой, совершаемой суммарным полем электростатич-х и сторонних сил при перемещ-и единичного полож-го заряда на данном участке цепи V12= φ1- φ2 + ε12. понятие напряжения явл-ся обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов, если на этом уч-ке не действует ЭДС, т.е. сторонние силы отсут-ют.
№25. Закон Ома. Сопротивление проводников. Немецкий физик Ом установил, что отнош-е напряжения к силе тока для данного проводника – величина постоянная и обозн-ся R. R= V/I – сопротивление. I= V/R – закон Ома для участка цепи(не содержащего источника тока): сила тока в проводнике прямо пропорц-на напряжению на концах и обратно пропорц-на сопротивлению проводника. Закон Ома для внутреннего источника: I =(ε –V)/ r. V= IR ; I = (ε –IR)/ r ; Ir = ε – IR ; ε = Ir + IR = I(r +R) ; I = ε /(r +R) – закон Ома для полной цепи, где ε – ЭДС, действующая в цепи, r – внутреннее сопротивл-е источника тока, R – сопротивл-е внешней цепи. 1/R =G – эл проводимость проводника. Исследуя проводники разл-х размеров и из разл-х материалов, Ом устан-л, что для однородных проводников сопротивление пропорц-но их длине и обратно пропорц-но площади сечения: R= ρl /S, где ρ – коэф-т пропорцион-ти – удельное эл сопротивл-е(сопрот-е проводника длиной 1м и площадью 1м2). γ = 1/ρ – удельная проводимость проводника. Учитывая, что V/l =E – напряженность эл поля в проводнике, I/S =j – плотность тока, закон Ома можно записать: j = γЕ – закон Ома в дифференц-ной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью эл поля в этой же точке. ρ = ρ0 (1+ αt ) – зав-ть сопротивл-я от температуры, ρ0 – удельно есопротивл-е при 0ºС, α – температурный коэф-т сопротивл-я (для всех чистых проводников, т.е. металлов, α близок к 1/273).
|
|
№27. Работа и мощность тока. Закон Джоуля-Ленца. Рассмотрим неодноодный проводник, к концам кот-го приложено напряжение V. За время dt ч/з сечение проводника переносится заряд dq = Idt. Т.к. ток предст-ет собой перемещ-е заряда под действием эл поля, то работа тока A= QV или dA= Vdq = IVdt. Если сопротивл-е проводника R, используя з-н Ома: dA= I2R dt = V2 dt /R. Мощность тока P= dA/dt = VI= I2R = V2/R. Работа – в джоулях, мощность – ваттах. Если
ток проходит по неподвижному металлич-му
проводнику, то вся работа тока идет
на его нагревание и, по з-ну сохранения
энергии: dQ=dA;
=> dQ=
IVdt
= I2Rdt
= V2
dt/
R
или Q=
R
I2
t
– закон Джоуля-Ленца – кол-во
выделяющегося в проводнике тепла
пропорц-но его сопротивл-ю, квадрату
силы тока и времени. Если I
измен-ся, то
|
№31. .Вращение рамки в магнитном поле Явление электромагнитной индукции применяется для преобразования мех. энергии в энергию электр. тока. Для этой цели используются генераторы, принцип действия которых можно рассмотреть на примере плоской рамки, вращающейся в однородном магнитном поле. Предположим, что рамка вращается в однородном магнитном поле (В= const) равномерно с угловой скоростью w=const. Магнитный поток, сцепленный с рамкой площадью S, в любой момент времени t равен Ф = BnS = BScos a = BScoswt, где a=wt — угол поворота рамки в момент времени t (начало отсчета выбрано так, чтобы при t=0 было а=0). При вращении рамки в ней будет возникать переменная э.дc. индукции Ei=-dФ/dt=BSwsin wt (1) изменяющаяся со временем по гармоническому закону. При sinwt=l э.д.с. Ei- максимальна, т. е. Emax=BSw (2) Учитывая (2), (1) м. записать Ei=Emax sin wt Т. о., если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная э.д.с, изменяющаяся по гармоническому закону. Из формулы (2) вытекает, что Е ш (следовательно, и э.дc. индукции) находится в прямой зависимости от величин w,B,S. В России принята стандартная частота тока v=w/(2П)=50 Гц, поэтому возможно лишь увеличение двух остальных величин. Для увеличения В применяют мощные постоянные магниты или в электромагнитах пропускают значительный ток, а также внутрь электромагнита помещают сердечники из материалов с большой магнитной проницаемостью ц. Если вращать не один, а ряд витков, соединенных последовательно, то тем самым увеличивается S. Переменное напряжение снимается с вращающегося витка с помощью щеток/. Процесс превращения механической энергии в электрическую обратим. Если по рамке, помещенной в магнитное поле, пропускать электрический ток, то на нее будет действовать вращающий момент и рамка начнет вращаться. На этом принципе основана работа электродвигателя, предназначенных для превращения электрической энергии в механическую.
|
|
|
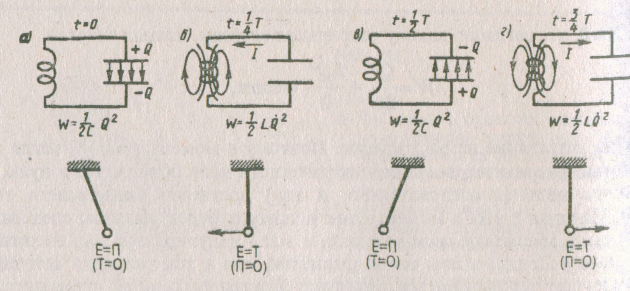
№33. Свободные гарм. колебания в колебат. контуре. Среди разл. электр. явлений особое место занимают электромагн. колебания, при которых электр. величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электр-го и магн-го полей. Для возбуждения и поддержания электромагн. колебаний используется колебательный контур — цепь, состоящая из включенных послед-но катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением JR. Рассм-м последовательные стадии колеб. пр-са в идеализированном контуре, сопротивление которого пренебрежимо мало (R примерно =0). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Тогда в начальный момент времени t=0 (рис. 202, а) между обкладками конденсатора возникнет электрическое поле, энергия которого 1/2C* Q2 (см. (95.4)). Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток. В резуль-те энергия электр. поля будет уменьшаться, а энергия магнитного поля катушки (она равна 1/2 LQ1) — возрастать. Так как R.≈Q, то, согласно закону сохранения энергии, полная энергия W=Q/2C(в кв.)+LQ(В кв)./2=const так как она на нагревание не расходуется. Поэтому в момент t=1/4Т, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения (рис. 202, б). Начиная с этого момента ток в контуре будет убывать; следовательно, начнет ослабевать магнитное поле катушки, и в ней индуцируется ток, который течет (согласно правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который в конце концов обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рве. 202, в). Далее те же процессы начнут протекать в обратном направлении (рас. 202, г) и система к моменту времени <= Г придет в первоначальное состояние (рис. 202, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. Если бы потерь энергии не было, то в контуре совершались бы периодические незатухающие колебания, т. е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, напряжение 17 на конденсаторе и сила тока /, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей. Электр. колебания в колебательном контуре можно сопоставить с механическими колебаниями маятника (рис. 202 внизу), сопровождающимися взаимными превращениями потенциальной и кинетической энергий маятника. В данном случае энергия электрического поля конденсатора (Q2/(2C)) аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ2/2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L играет роль массы т, а сопротивление контура — роль силы трения, действующей на маятник. Согласно закону Ома, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор сопротивлением R, IR+Uc=εs где IR — напряжение на резисторе, UC=Q/C — напряжение на конденсаторе, εs =-L dI/dt-эдс самоиндукции, возникающая в катушке при протекании в ней переменного тока (εs — единственная э.д.с. в контуре). Следовательно, L dI/dt+IR+Q/C=0 (1) Разделив (1) на L и подставив I= Q’ и dI/dT = Q”, получим дифф. уравнение колебаний заряда Q в контуре: Q``+R/LQ`+1/LC*Q=0 В данном колебательном контуре внешние э.д.с. отсутствуют, поэтому рассмат- риваемые колебания представляют собой свободные колебания (см. § 140). Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда из (143.2) получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре: Q``+1/LC=0 Из выражений (142.1) и (140.1) вытекает, что заряд Q совершает гармонические колебания по закону Q=Qm cos (Wot+ф) 143.3 где Qm — амплитуда колебаний заряда конденсатора с циклической частотой wo, называемой собственной частотой контура, т. е. wo=1/ кореньLC 143.4 и периодом Т =2п/ корень LC 143.5 Формула (143.5) впервые было получена У. Томсоном и называется формулой Томсона.
|
19. Закон сохранения электрического заряда. З-н Кулона. Электростатическое поле. Изучая эл.заряд ученые пришли к выводу, что они состоят из отдельных элемент.зарядов. В 1843 г. Англ. физиком М. Фарадеем закон сохранен. заряда: алгебр-ая сумма эл. зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы. Электрический заряд — величина релятивистски инвариантная, т.е. не зав-т от системы отсчета и от того, движется этот заряд или покоится. В зав-ти от конц-ции свободных зарядов тела делятся на проводники, диэлектрики и полупроводники. Проводники — тела, в к-ых эл. заряд может перемещаться по всему его объему. Диэлектрики (н-р, пластмассы, стекло) — тела, в к-ых практически отсутствуют свободные заряды. полупроводники (н-р, германий, кремний) занимают промежуточное положение , м\у проводниками и диэлектриками. Ед-ца эл. заряда − кулон (Кл) — эл. заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1с. Закон Кулона Точечным наз-ся заряд, сосредоточенный на теле, линейные размеры кот-ого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с к-ыми он взаимод-ет. Сила взаимод-ия F м\у двумя неподвижными точеч-ми зарядами наход-ся в вакууме, пропорц-на зарядам Q1 и Q2 и обратно пропорц-на квадрату расстояния г м\у ними: F = (k |Q1 − Q2|) /r2 Где k- коэф-т пропорц-ти , зав-щий от выбора системы ед-ц. Сила F направлена по прямой соед-щей взаимод-щие заряды, т.е. явл-ся центральной, и соотв-ет притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в сл-ае одноименных зарядов. Эта сила наз-ся Кулоновской силой где F12 - сила, действующая на заряд Q1 со стороны заряда Q2 ,r12 — радиус-вектор, соединяющий заряд Q1 с зарядом Q2 , r = | r12|. На заряд Q1 со стороны заряда Q2 действует сила F21 = -F12. Величина Е0 наз-ся Эл-кой пост-ной и равна Е0 = 8.85*10-12 Кл2/(Н*м2) или Ф/м, где фарад(Ф) – ед-ца Эл-кой емкости. Тогда 1/ 4пE0 = 9 * 10-9м/Ф Если в простр-во, окр-щее эл-кий заряд, ввести др. заряд, то на него будет действовать кулоновская сила; зн-т, в простр-ве, окр-щем эл. заряды, сущ-ет силовое поле. В данном сл-е говорят об электрическом поле — поле, посредством к-ого взаимод-ют эл-ие заряды. Мы будем рассм-вать эл-ие поля, к-ые созд-ся неподвижными эл-ими зарядами и наз-ся электростат-ими. Для обнаружения и опытного исслед-ия ЭП исп-ется пробный точечный “+“ заряд — такой заряд, который не искажает иссл-ое поле (не вызывает перераспред-ния зарядов, созд-их поле). Если в поле,созд-емое зарядом Q поместить пробный заряд Qо, то на него действует сила F различная в разных точках поля, к-ая, согласно закону
Кулона (F = (1/ 4пE0)*(Q1 Q2 /r2 )), пропорц-на пробному заряду Q0. Поэтому отношение F/Q0 не зависит от Qо и хар-ует ЭП в той точке, где пробный заряд нах-ся. Эта величина наз-ся напряженностью и явл-ся силовой хар-кой ЭП. Напряж-сть ЭП в данной точке есть физ-кая величина, опр-емая силой, действующей на пробный ед-чный “+“ заряд, помещенный в эту точку поля: E =F / Q0 (1) Как следует из ф-ул (1) и (2), напряж-ть поля точечного заряда в вакууме (2) E = (1/ 4пE0)*(Q/r2) Напр-ние вектора Е совпадает с напр-нем силы, действующей на “+“ заряд. Если поле создается “+“зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного “+“ заряда); если поле создается “-“зарядом, то вектор Е направлен к заряду Из ф-лы (1) следует, что ед-ца напряж-ти ЭП – (Н/Кл): 1 Кл действует с силой в 1 Н; 1 Н/Кл=1 В/ м, где В(вольт)- ед-ца потенциала ЭП.
|
№23. Электр. ток, сила и плотность тока. Электр. током наз-ют люб. упорядоченное (направл
е Для возн-ния и существ-ния электр. тока необх-мо, с одной стороны, наличие своб. носителей тока – заряженных частиц, способных перемещаться упорядоченно, а с другой – наличие электр. поля, энергия кот-го каким-то образом восполнялась, расходовалось бы на их упорядочен. движение. За напр-ние тока условно принимают напр-ние движения положит. зарядов. Количеств. мерой электр. тока служит сила тока I – скалярная физ. вел-на, определяемая электр. зарядом, порходящим ч/з поперечн. сечение пров-ка в ед-цу времени: I=dQ/dt Если сила тока и его напр-ние не измен-ся со временем, то такой ток наз-ся постоянным. Для пост. тока: I=Q/t, где Q – электр. заряд. проходящий за время t ч/з поперечное сечениепроводника. Изм-ся в Амперах. Физ величина, определяемая силой тока, проходящего ч/з ед-цу площади поперечн. сечения пров-ка, перпенд-го напр-ю тока, наз-ся плотностью тока: j=dI/dS┴ . Выразим силу и плотность тока ч/з скорость (v) упоряд. дв-ния зарядов в проводнике.Если конц-ция носителей тока равна n и каждый день носитель имеет элемент. заряд e (что не обяз-но для ионов), то за время dt ч/з поперечное сечение S пров-ка переносится заряд dQ=ne(v)Sdt Плотность тока – вектор ориентированный по напр-ию тока. т.е. напр-ие вектора j совпадает с напр-ем упорядоченного движения положит. зарядов. Ед-ца плотности тока- А/м2.
Сила тока сквозь
произвольную поверх-сть S
опр-ся как поток вектора j,
т.е.
Где dS=ndS (n – единичный вектор нормали к площадке dS, составляющей с вектором j угол α).
|
|
|
|
|
|
|
|
|
|
|
|
|

 торое
правило Кирхгофа получается из
обощенного закона Ома для разветвленных
цепей ( IR=(φ1-φ2)+ε12
). Рассм-м
контур, состоящий из 3 участков (рис.2).
Напр-ие обхода по час. стрелке примем
за полож-ое, отметив, что выбор этого
напр-ия совершенно производен. Все
токи. совпадающие по напр-ию с напр-ем
обхода контура, считаются положительными,
не совпадающие с напр-ем обхода-
отриц-м. Источники тока считаются
полоиж-ми, если они создают ток, напрвл-й
в сторону обхода контура. Применяя к
участкам з-н Ома м. записать:
торое
правило Кирхгофа получается из
обощенного закона Ома для разветвленных
цепей ( IR=(φ1-φ2)+ε12
). Рассм-м
контур, состоящий из 3 участков (рис.2).
Напр-ие обхода по час. стрелке примем
за полож-ое, отметив, что выбор этого
напр-ия совершенно производен. Все
токи. совпадающие по напр-ию с напр-ем
обхода контура, считаются положительными,
не совпадающие с напр-ем обхода-
отриц-м. Источники тока считаются
полоиж-ми, если они создают ток, напрвл-й
в сторону обхода контура. Применяя к
участкам з-н Ома м. записать: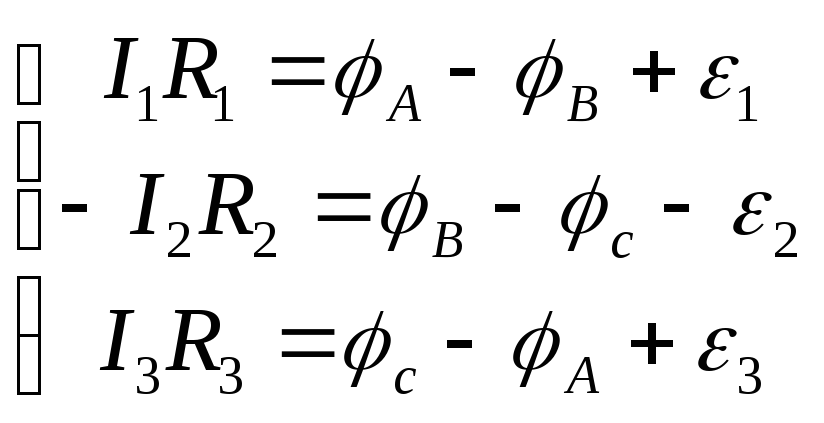
 -
вектор, модуль которого равен элементу
проводника dl.
-
вектор, модуль которого равен элементу
проводника dl.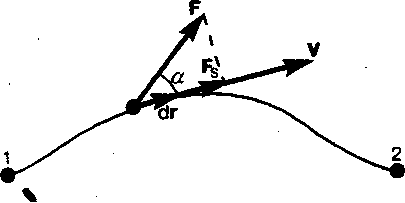
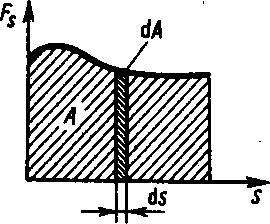 ля
выч-ния этого интеграла н. знать зав-сть
силы Fs
от
пути 5 вдоль траектории 1
— 2. Пусть
эта зав-сть представлена граф-ски,
тогда искомая
работа А
опр-ся
на графике площадью заштрих-й фигуры.
Если, напр-р, тело движется прямолинейно,
сила F=соnst
и α=соnst,
то получим
ля
выч-ния этого интеграла н. знать зав-сть
силы Fs
от
пути 5 вдоль траектории 1
— 2. Пусть
эта зав-сть представлена граф-ски,
тогда искомая
работа А
опр-ся
на графике площадью заштрих-й фигуры.
Если, напр-р, тело движется прямолинейно,
сила F=соnst
и α=соnst,
то получим