А.3 Анализ однородности ряда, содержащего максимальные расходы воды разного генетического происхождения

Ряд наблюдений за максимальными расходами воды р. Абавы у х. Сисени включает 21 расход воды весеннего половодья и 15 расходов дождевых паводков. Оценку однородности средних значений и дисперсий при сравнении двух генетически разнородных выборок осуществляют по критериям Стьюдента и Фишера. Вычисленные расчетные значения статистик критериев соответственно равны: t = 2,52 и F = 1,09. Критические значения статистик F* и t* определяют из таблиц [3] путем интерполяции между табличными значениями при n_x = n_y = 10 и п_x = п_y =25 для заданного уровня значимости a = 5 %, коэффициента автокорреляции r(1) = 0,2 и коэффициента межрядной корреляции R = 0. В результате получены критические значения t* = 2,04 (для n_x = n_у = 21), t* = 2,06 (для n_x = n_у = 15) и F* = 2,31. При сравнении с расчетными значениями статистик можно сделать вывод, что ряд наблюдений не может рассматриваться как единая совокупность вследствие неоднородности средних значений, так как расчетное значение статистики Стьюдента превышает критическое в обоих случаях (n = 15 и n = 21), при этом гипотеза об однородности дисперсий не отклоняется. Поэтому расчеты необходимо осуществлять отдельно для рядов весеннего половодья и дождевых паводков.

А.4 Оценка эффективности эмпирической зависимости

Для расчетов годового стока и слоя стока весеннего половодья при отсутствии данных гидрометрических наблюдений применяют зависимости от стокоформирующих факторов. Одной из таких существующих зависимостей является уравнение для определения слоя поверхностного стока весеннего половодья Y на р. Оке — с. Половское следующего вида:

Y = 0,80Х₁ + 0,86Х₂ - 104, (А.1)

где X₁ = S + S_л + X_ос;

S — максимальные запасы воды в снеге, мм;

S_л — запас воды в ледяной корке, мм;

X_ос — осадки за период половодья, мм;

X₂ = (L · e)/50;

здесь L — глубина промерзания почвы, см;

e — величина осеннего увлажнения почвы, см.

Для оценки эффективности эмпирической зависимости в соответствии с 4.15 применен анализ остатков и построены графики, приведенные на рисунке А.1.

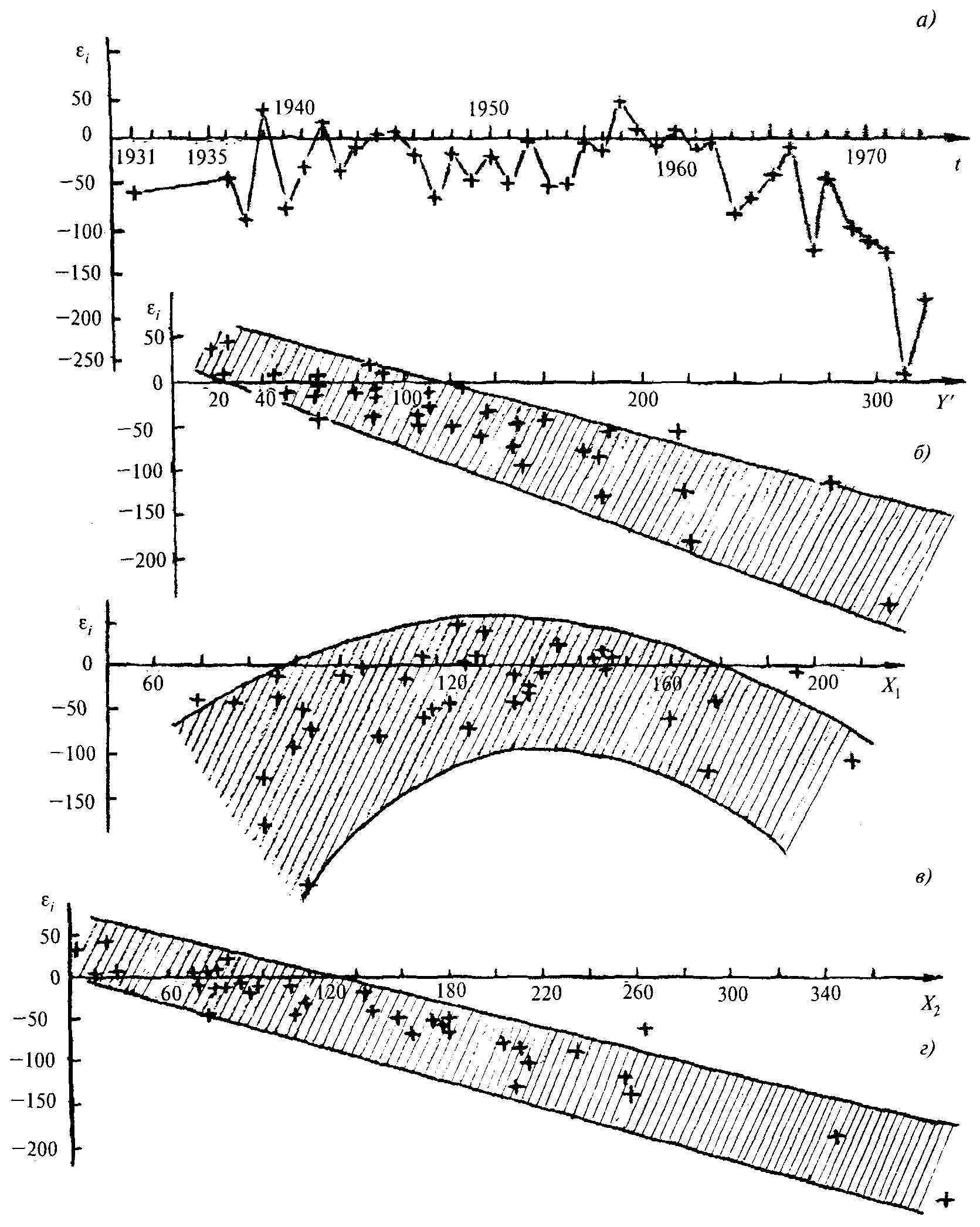
а) — зависимость остатков от времени (e = f(t)); б) — зависимость остатков от значений слоя стока, полученного по эмпирической зависимости (e = f(Y')); в) — зависимость остатков от первого фактора (e = f(Х₁)); г) — зависимость остатков от второго фактора (e = f(X₂))

Рисунок A.1 — Анализ остатков эмпирической зависимости для расчета слоев половодья

от метеорологических факторов

Из анализа графиков на рисунке А.1 можно сделать следующие выводы:

- с 1967 г. остатки зависят от времени и имеет место существенное систематическое завышение слоя стока половодья, вычисленного по эмпирической зависимости (рисунок А.1, а);

- наклонная полоса рассеяния на рисунке А.1, б показывает, что отклонения от полученной эмпирической зависимости носят систематический характер: отрицательные остатки соответствуют большим по величине значениям расчетных слоев стока, положительные — малым, что свидетельствует о неточном определении свободного члена в уравнении;

- изгиб полосы рассеяния на рисунке А.1, в показывает, что в уравнении необходимо учесть нелинейность зависимости Y от Х₁;

- из рисунка А.1, г следует, что коэффициент перед Х₂ также определен неверно.

Для уточнения вида и коэффициентов уравнения была собрана дополнительная информация, проведен анализ однофакторных зависимостей и использованы условия построения регрессионного уравнения (6.1). В результате получена следующая эмпирическая зависимость:

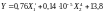, (А.1, а)

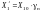где , здесь Х₁₀ — средний максимальный снегозапас в бассейне, мм, осредненный по 10 метеостанциям, для которых коэффициент корреляции снегозапасов со стоком половодья больше 0,5;

g_п = K_п·b_п, здесь K_п — модульный коэффициент приведенных запасов влаги в почве;

b_п = sin(a' + 10°), tg a' = K_H, здесь K_H — модульный коэффициент промерзания;

Х₂ — слой стока за март, мм.

Коэффициент корреляции полученного уравнения равен 0,89. Анализ остатков показал, что полученное эмпирическое уравнение является адекватным.