17. Формулы площадей треугольников, четырёхугольников (общего и частных видов), круга и его частей.

Треугольник:

1. Произвольный треугольник

a, b, c — стороны;  — угол между сторонами a и b; — полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; h_a — высота, проведенная к стороне a.

S = ah_a, S = ab sin , , S = pr,

2. Прямоугольный треугольник

a, b — катеты; c — гипотенуза; h_c — высота, проведенная к стороне c.

S = ab, S = ch_c

3. Равносторонний треугольник

Четырехугольники:

1. Произвольный выпуклый четырехугольник d₁, d₂ — диагонали; 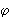— угол между ними; S — площадь. S = d₁d₂ sin

2. Параллелограмм a и b — смежные стороны; — угол между ними; h_a — высота, проведенная к стороне a.

S = ah_a, S = ab sin , S = d₁d₂ sin

3. Трапеция a и b — основания; h — расстояние между ними; l — средняя линия.

, S = lh

4. Прямоугольник

S = ab, S = d₁d₂ sin

5. Ромб

S = ah_a, S = a²sin , S = d₁d₂

6. Квадрат d — диагональ.

S = a² S = d²

Окружность:

Площадь круга равна половине произведения длины ограничивающей ее окружности на радиус:

Площадь кругового сектора вычисляется по формуле 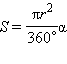, где r – радиус окружности, α – градусная мера соответствующего центрального угла.

Площадь сегмента, не равного полукругу, вычисляется по формуле 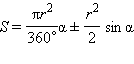, где r – радиус окружности, α – градусная мера соответствующего центрального угла, ограничивающего сегмент. Знак «+» выбирается, если α < 180º; знак «–» – если α > 180º.

18. Теоремы об отношениях площадей подобных треугольников и треугольников, имеющих общие или равные элементы.

    1. Площади подобных треугольников (и вообще любых фигур) относятся, как квадраты их линейных размеров

    2. Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих

треугольников равно отношению произведений сторон, заключающих равные углы