
- •Министерство образования украины
- •Донецкий государственный
- •Технический университет
- •Методические указания
- •Утверждено На заседании каф.Пм и и
- •Часть1.Решение типовых задач аналитической геометрии
- •Часть 1. Решение типовых задач аналитической геометрии……………3
- •Часть 2. Расчетные задания………………………………………………17
- •Учебное издание
- •Министерство образования украины
- •Донецкий государственный
- •Технический университет
- •Методические указания
- •Утверждено На заседании каф.Пм и и
- •22 Марта 2000 г.
Министерство образования украины
Донецкий государственный
Технический университет
Методические указания
и задания к расчетно-графической работе
по разделу курса высшей математики
«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
(для студентов специальностей 7.080403
«Программное обеспечение автоматизированных систем»
и 7.050102 «Экономическая кибернетика»)
Утверждено На заседании каф.Пм и и
22 марта 2000 г.
-ДонГТУ-
Донецк - 2000
УДК 517
Методические указания и задания к расчетно-графической работе по разделу курса высшей математики «Аналитическая геометрия» (для студентов специальностей 7.080403 “Программное обеспечение автоматизированных систем” и 7.050102 “Экономическая кибернетика” ) / Составители: Скворцов А.Е., Губарев А.А
– Донецк : ДГТУ , 2000.- с.30
Приведены решения типовых задач по всем темам раздела «Аналитическая геометрия».Даны рекомендации общего и конкретного характера . Приведены расчетные задания : 12 задач по 25 вариантов .
Составители А.Е. Скворцов , доц .
А.А. Губарев , асс.
Отв.за выпуск Е.А. Башков , проф.
Рецензент
Часть1.Решение типовых задач аналитической геометрии
Задача
1. Какому
условию должны удовлетворять векторы
![]() и
и
![]() , чтобы имело место соотношение
, чтобы имело место соотношение
![]() ?
?
Решение. Возведем обе части данного равенства в квадрат и воспользуемся известным фактом : скалярный квадрат вектора равен квадрату его длины . Будем иметь:
![]() .
.
Но для скалярного произведения справедливы формулы сокращенного умножения , поэтому после упрощения получим
![]() .
.
По
определению
![]() φ
, где φ- угол между векторами . Сравнивая
это определение с последней формулой
, делаем вывод : cos
φ = -1 т.е. φ = π , значит векторы противоположно
направлены . Кроме того ,
φ
, где φ- угол между векторами . Сравнивая
это определение с последней формулой
, делаем вывод : cos
φ = -1 т.е. φ = π , значит векторы противоположно
направлены . Кроме того ,
![]() , значит
не короче
.
, значит
не короче
.
Ответ : ↑↓ и ≥ .
Задача 2. Найти вектор , направленный по биссектрисе угла , образованного векторами и .
Решение. Сумма векторов – это одна из диагоналей параллелограмма , построенного на векторах . Но в общем случае диагональ параллелограмма не является биссектрисой его углов . Чтобы это было так , параллелограмм должен быть ромбом , т.е. векторы-слагаемые должны иметь равные длины . Перейдем к ортам векторов и , для чего разделим эти векторы на их длины :
![]() ,
,
![]() .
.
Направления ортов совпадают с направлениями самих векторов (т.к. векторы делятся на положительные числа ) , а длины одинаковы . Значит сумма ортов , как диагональ ромба , направлена по биссектрисе угла , образованного ими , т.е. по биссектрисе угла , образованного векторами и .
Ответ
: искомый
вектор имеет вид
![]() +
+
![]() .
.
Задача
3. Векторы
и
- взаимно перпендикулярные орты . Выяснить
при каких значениях параметра t
векторы
![]() и
и
![]() : 1)перпендикулярны; 2) коллинеарны .
: 1)перпендикулярны; 2) коллинеарны .
Решение.
Будем
использовать известные условия
![]() ,
,
![]() .
.
Напомним
, что при скалярном и векторном умножении
векторных “многочленов” скобки
раскрываем обычным образом , учитывая
следующее : скалярный квадрат вектора
– это квадрат его длины , “векторный”
квадрат – это всегда нуль-вектор,
скалярное умножение коммутативно , а
векторное антикоммутативно
![]() .
.
Итак , имеем :
![]() ,
,
![]() , ибо
, ибо
![]() ;
;
![]() .
.
Из полученных соотношений делаем выводы :
векторы
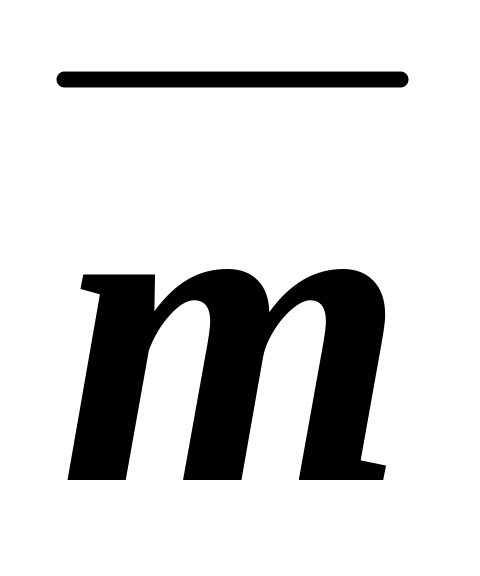 и
и
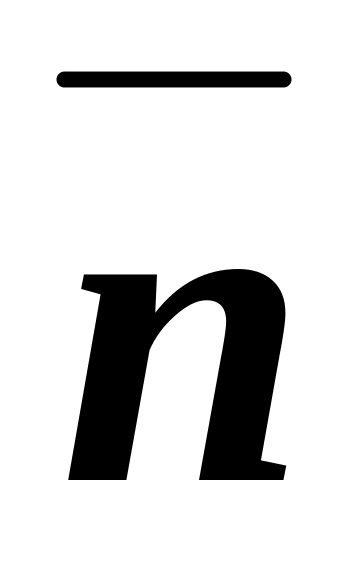 перпендикулярны , если t
–2=0 , т.е.
t=2
;
перпендикулярны , если t
–2=0 , т.е.
t=2
;векторы коллинеарны , если 2 t+1=0 ,т.е. t=-1/2
![]() ,
ибо
и
неколлинеарны .
,
ибо
и
неколлинеарны .
Замечание.
На второй
вопрос задачи можно ответить и другим
образом . Коллинеарность векторов
и
означает
= λ
, где λ - некоторое число , т.е.
![]() или
или
![]() . Но векторы
и
- неколлинеарны, значит образуют базис
, поэтому разложение любого вектора ( в
частности ,вектора
. Но векторы
и
- неколлинеарны, значит образуют базис
, поэтому разложение любого вектора ( в
частности ,вектора
![]() )
по
и
единственно , другими словами , коэффициенты
двух равных линейных комбинаций
и
равны : 1= λ
t
и 2=- λ .
Отсюда t=-1/2.
)
по
и
единственно , другими словами , коэффициенты
двух равных линейных комбинаций
и
равны : 1= λ
t
и 2=- λ .
Отсюда t=-1/2.
Ответ
:
![]() при t=2
;
при t=2
;
![]() при t=-0,5
.
при t=-0,5
.
Задача
4. Найти
вектор
![]() , удовлетворяющий условиям : 1)
, удовлетворяющий условиям : 1)![]() и
и
![]() ;
2)
;
2)
![]() ;
3)
образует с осью Оу тупой угол .
;
3)
образует с осью Оу тупой угол .
Решение
. Из первого
условия следует , что искомый вектор
коллинеарен векторному произведению
![]() , ибо по определению
- это вектор , перпендикулярный каждому
из векторов-сомножителей . Вычисляем
по известной формуле
, ибо по определению
- это вектор , перпендикулярный каждому
из векторов-сомножителей . Вычисляем
по известной формуле
 ,
,
где
![]() ,
,
![]() :
:
![]()
![]()
![]() .
.
Итак
,
![]() , т.е.
, т.е.
![]() , где
, где
![]() .
.
Далее , используя второе условие , находим
![]() ,
,
![]() , т.е.
, т.е.
![]() .
.
Чтобы
определить знак множителя λ , обратимся
к третьему условию , которое означает
, что проекция искомого вектора на ось
Оу отрицательна . А так как проекция
вектора
![]() на ось Оу положительна , то λ<0
.Окончательно , λ =-2 и искомый вектор
имеет вид
на ось Оу положительна , то λ<0
.Окончательно , λ =-2 и искомый вектор
имеет вид
![]() .
.
Замечание.
Условия
задачи можно использовать и другим
способом . Например : так как
![]() , то
, то
![]() , т.е.
3x+2y+2z=0
; а равенство
означает
, т.е.
3x+2y+2z=0
; а равенство
означает
![]() (здесь x,y,z-
проекции искомого вектора). При этом
пришлось бы решать нелинейную систему
из трех уравнений с тремя неизвестными.
(здесь x,y,z-
проекции искомого вектора). При этом
пришлось бы решать нелинейную систему
из трех уравнений с тремя неизвестными.
Ответ:
![]() .
.
Задача 5. Даны вершины треугольника : А(-1;-2) , В(4;7) , С(-4;2) . Требуется: 1) составить уравнение и найти длину биссектрисы AD угла треугольника при вершине А ; 2) составить уравнение и найти длину высоты AH , опущенной из вершины А на противоположную сторону ; 3) найти площадь треугольника S .
Решение . Уравнение биссектрисы будем искать в канонической форме , а именно :
![]() ,
где
,
где
![]() - точка , принадлежащая прямой р,
- точка , принадлежащая прямой р,
![]() - направляющий вектор прямой р
. В качестве точки
- направляющий вектор прямой р
. В качестве точки
![]() возьмем вершину А , а в качестве
направляющего вектора – вектор ,
направленный по биссектрисе угла,
образованного векторами
возьмем вершину А , а в качестве
направляющего вектора – вектор ,
направленный по биссектрисе угла,
образованного векторами
![]() и
и
![]() ( смотри задачу 2) . Найдем сначала эти
векторы и их длины , используя известные
формулы : если
( смотри задачу 2) . Найдем сначала эти
векторы и их длины , используя известные
формулы : если
![]() , то
, то
![]() ; если
; если
![]() , то
, то
![]() .
Для нашей задачи имеем :
.
Для нашей задачи имеем :
![]()
![]()
Вектор
![]() направлен по биссектрисе угла ,
образованного векторами
и
направлен по биссектрисе угла ,
образованного векторами
и
![]() .
Находим его :
.
Находим его :
![]() .
.
Но
векторы вида
и
![]() - коллинеарны , т.е. являются направляющими
векторами одной и той же прямой . Поэтому
в качестве направляющего вектора
биссектрисы AD
можно взять вектор
- коллинеарны , т.е. являются направляющими
векторами одной и той же прямой . Поэтому
в качестве направляющего вектора
биссектрисы AD
можно взять вектор
![]() . Итак , уравнение биссектрисы имеет вид
:
. Итак , уравнение биссектрисы имеет вид
:
![]() , или после упрощения
, или после упрощения
AD : 7x – y + 5 =0 .
Длину
биссектрисы найдем как расстояние от
вершины А до точки пересечения D
биссектрисы с противоположной стороной
. Составим сначала уравнение стороны
ВС, как уравнение прямой , проходящей
через две точки![]() :
:
![]() .
.
Берем
![]() и
и
![]() . Получаем :
. Получаем :
![]() или
после упрощения
или
после упрощения
ВС : 2x – 11y + 30 = 0 .
Координаты точки D - это решение системы линейных уравнений
![]() или
или
![]()
Решив ее , например , методом Крамера ,
![]() ,
,
![]() ,
,
получим D (-1/3 ; 8/3 ) . Тогда искомая длина биссектрисы равна
AD
= d(A,D) =
![]() .
.
Замечание. Эту часть задачи можно решать в ином порядке . Сначала можно найти координаты точки D , используя известный из элементарной геометрии факт : точка D делит сторону ВС в отношении λ = BD/DC = AB/AC . В нашей задаче λ=10/5 = 2 . Теперь координаты точки , делящей отрезок в заданном отношении , находим по формулам
![]() ,
,
![]() .
.
Теперь уравнение биссектрисы находим как уравнение прямой , проходящей через две точки .
2)Длину высоты АН , опущенной из вершины А , находим как расстояние от точки А до прямой ВС . Общая формула :
![]() ,
где
,
где
![]() .
.
Имеем в нашей задаче :
АН=![]() .
.
Уравнение высоты ищем в общем виде :
![]() , где
, где
![]() - нормальный вектор прямой р . В нашем
случае
- нормальный вектор прямой р . В нашем
случае
![]() , а
, а
![]() :
:
АН : -11 (x + 1)-2 (y + 2) = 0 или после упрощения
AH : 11 x + 2 y + 15 = 0 .
Замечание.
Из уравнения прямой ВС (полученного
ранее) легко найти нормальный вектор
этой прямой :
![]() . Для высоты АН этот вектор является
направляющим и уравнение АН можно
находить в канонической форме :
. Для высоты АН этот вектор является
направляющим и уравнение АН можно
находить в канонической форме :
![]() .
.
3)Для
вычисления площади треугольника
используем геометрический смысл
:
длина векторного произведения двух
векторов есть площадь параллелограмма
, построенного на этих векторах . А
площадь треугольника – это половина
площади параллелограмма . Векторы
![]() и
и
![]() мы уже знаем . Находим их векторное
произведение :
мы уже знаем . Находим их векторное
произведение :
![]() .
.
Итак ,
![]() (ед.кв.) .
(ед.кв.) .
Замечание. Этот способ вычисления площади треугольника является наиболее рациональным в случае , когда известны координаты его вершин .
Задача 6. Определить параметры , входящие в уравнения прямых и плоскостей, используя данные об их взаимном расположении : 1) прямые
![]() и
и
![]()
пересекаются
под прямым углом ; 2) для точки
![]() , плоскости
, плоскости
![]() и прямой
и прямой
![]() известно , что
известно , что
![]() и
и
![]() .
.
Решение
. 1)Общий вид
канонических и параметрических уравнений
прямой :
![]() и
и
![]()
В
этих уравнениях :
![]() - точка , принадлежащая прямой ,
- точка , принадлежащая прямой ,
![]() - направляющий вектор прямой (т.е. вектор
, лежащий на прямой , или параллельный
ей ) . Из условий задачи сразу получаем
:
- направляющий вектор прямой (т.е. вектор
, лежащий на прямой , или параллельный
ей ) . Из условий задачи сразу получаем
:
![]()
![]()
Условие
![]() означает , что
означает , что
![]() , т.е.
, т.е.
![]() . Отсюда :
. Отсюда :
![]() , значит l
= 1 .Тот факт , что p
и q
пересекаются означает , что эти прямые
определяют некоторую плоскость и в этой
плоскости лежат или параллельны ей
векторы
, значит l
= 1 .Тот факт , что p
и q
пересекаются означает , что эти прямые
определяют некоторую плоскость и в этой
плоскости лежат или параллельны ей
векторы
![]() и
и
![]() . Другими словами , эти векторы компланарны
, а значит их смешанное произведение
равно 0 :
. Другими словами , эти векторы компланарны
, а значит их смешанное произведение
равно 0 :
![]() .
.
Отсюда
![]() . Параметры найдены .
. Параметры найдены .
2)Известно
, что в общем уравнении плоскости
![]() коэффициенты при переменных – это
координаты нормального вектора плоскости
(т.е. вектора перпендикулярного ей ) . В
нашем случае нормальный вектор плоскости
α
имеет вид
коэффициенты при переменных – это
координаты нормального вектора плоскости
(т.е. вектора перпендикулярного ей ) . В
нашем случае нормальный вектор плоскости
α
имеет вид
![]() . Из уравнений прямой р
получаем :
. Из уравнений прямой р
получаем :
![]() - направляющий вектор прямой ,
- направляющий вектор прямой ,
![]() - точка , принадлежащая прямой .
- точка , принадлежащая прямой .
Отличное
от нуля расстояние
![]() означает , что
означает , что
![]() , т.е.
, т.е.
![]() . Отсюда получим :
. Отсюда получим :
![]() , значит А=2 .
, значит А=2 .
Теперь
воспользуемся известными формулами
для расстояния от точки до прямой и
плоскости ( очевидно , что
=
![]() ):
):
![]() ,
,
![]() .
.
Вычислим эти расстояния :
![]() ;
;
![]() ;
;
![]() ;
;
=
![]() .
.
Приравняв полученные выражения к числам , данным в условии задачи , получим систему двух уравнений с одним неизвестным :
![]()
Решениями
первого уравнения являются числа
![]() . Но второму уравнению удовлетворяет
только значение
. Но второму уравнению удовлетворяет
только значение
![]() . Итак , параметры , входящие в уравнения
, найдены А
= 2 , t
= -1 .
. Итак , параметры , входящие в уравнения
, найдены А
= 2 , t
= -1 .
Задача
7. Составить
уравнение плоскости α
, если известно
, что 1) :
![]() и
и
![]() , где
, где
![]() ; 2) α проходит
через точку пересечения прямой
; 2) α проходит
через точку пересечения прямой
![]() и плоскость
и плоскость
![]() , причем
, причем
![]() .
.
Решение
. Наиболее
общий прием составления уравнения
плоскости состоит в следующем . Берем
произвольную (текущую) точку искомой
плоскости , т.е. точку с переменными
координатами M(x,y,z)
. Далее находим три вектора
![]() ,лежащие в искомой плоскости или
параллельны ей , причем конец одного из
них – это текущая точка М , и векторы
попарно неколлинеарны . Записываем
условие компланарности этих векторов
, т.е.
,лежащие в искомой плоскости или
параллельны ей , причем конец одного из
них – это текущая точка М , и векторы
попарно неколлинеарны . Записываем
условие компланарности этих векторов
, т.е.
![]() .
Это и будет уравнение искомой плоскости
.
.
Это и будет уравнение искомой плоскости
.
Если
же известны некоторый вектор
![]() , перпендикулярный искомой плоскости
, и точка
, перпендикулярный искомой плоскости
, и точка
![]() , принадлежащая ей , то уравнение такой
плоскости имеет вид
, принадлежащая ей , то уравнение такой
плоскости имеет вид
![]() .
.
1)Из
канонических уравнений прямых находим
их направляющие векторы
![]() и точки
и точки
![]() , принадлежащие соответствующим прямым
. Берем текущую точку
, принадлежащие соответствующим прямым
. Берем текущую точку
![]() . Так как
. Так как
![]() , то вектор
, то вектор
![]() лежит в плоскости α
. Далее ,так
как по условию
лежит в плоскости α
. Далее ,так
как по условию
![]() и
, то
и
, то
![]() и
и
![]() . Итак , у нас есть требуемая тройка
компланарных векторов . Находим их
смешанное произведение
. Итак , у нас есть требуемая тройка
компланарных векторов . Находим их
смешанное произведение
![]() .
.
Приравняем это выражение к нулю и после упрощения получим уравнение искомой плоскости α : 23x – 16y + 10z – 153 = 0 .
2)Так
как
, то направляющий вектор прямой р является
одним из нормальных векторов плоскости
α :
![]() . Теперь найдем точку пересечения
плоскости и прямой . Для этого запишем
уравнения прямой в параметрическом
виде, обозначив каждое из трех отношений
, составляющих канонические уравнения
, через t
:
. Теперь найдем точку пересечения
плоскости и прямой . Для этого запишем
уравнения прямой в параметрическом
виде, обозначив каждое из трех отношений
, составляющих канонические уравнения
, через t
:
![]() или
или
![]()
Подставив
эти уравнения в уравнение плоскости β
, получим
![]() , откуда t
= -3 . Это значение параметра соответствует
точке пересечения . Её координаты
, откуда t
= -3 . Это значение параметра соответствует
точке пересечения . Её координаты
![]() ,
,
![]() и
и
![]() .
.
Составляем
общее уравнение плоскости проходящей
через точку
![]() с нормальным вектором
:
с нормальным вектором
:
![]() .
.
После упрощения получим
![]() .
.
Задача 8. Даны вершины треугольника А(1;2;-1) , В(7;9;-3) и С(4;8;8) . Составить каноническое уравнение его высоты , опущенной из вершины В на противоположную сторону .
Решение
. Спроектируем
вершину В на сторону АС (или ее продолжение)
, для чего через точку В проведем плоскость
α
, перпендикулярную стороне АС .Для этой
плоскости вектор
![]() является нормальным . Поэтому уравнение
плоскости α
имеет вид
является нормальным . Поэтому уравнение
плоскости α
имеет вид
![]() ,
,
или после упрощения
α
:
![]() .
.
Проекцией
точки В на сторону АС является точка
пересечения плоскости α
и прямой р , на которой лежит сторона АС
. Для этой прямой р вектор
![]() является направляющим вектором . Зная
, что р проходит через точку А(1;2;-1) , можно
составить параметрические уравнения
р :
является направляющим вектором . Зная
, что р проходит через точку А(1;2;-1) , можно
составить параметрические уравнения
р :
![]()
Найдем точку пересечения р и α :
![]() ,
,
откуда t =1/3 , x=1+1 = 2 , y = 2+2 = 4 , z = -1+3 = 2 .
Итак , проекция точки В на АС , т.е. основание высоты имеет координаты D(2;4;2) . Составим уравнения высоты AD как уравнения прямой , проходящей через две точки. Общий вид таких уравнений
![]() .
.
В нашей задач имеем
![]() .
.
После упрощения получим требуемые уравнения высоты треугольника
![]() .
.
Замечание.
Эту задачу можно решить и другим способом
, заметив , что высота BD
является линией пересечения двух
плоскостей , а именно : плоскости α
, проходящей через точку В перпендикулярно
АС и плоскости β
, проходящей через вершины треугольника
. Уравнение плоскости β
можно легко найти , используя общий
прием. Если M(x,y,z)–
текущая точка β
, то векторы
![]() и
лежат в β.
и
лежат в β.
Записав
условие компланарности этих векторов
![]() , получим уравнение β
. Объединив уравнения плоскостей α
и β
в систему , получим общие уравнения
высоты BD
(переход от общих уравнений к каноническим
разобран в следующей задаче ) .
, получим уравнение β
. Объединив уравнения плоскостей α
и β
в систему , получим общие уравнения
высоты BD
(переход от общих уравнений к каноническим
разобран в следующей задаче ) .
Задача
9. Найти
канонические уравнения проекции q прямой
![]() на плоскость α
:
на плоскость α
:
![]() .
.
Решение
. Найдем
уравнение проектирующей плоскости β
, т.е. плоскости , содержащей в себе прямую
р
, и перпендикулярной плоскости α
.Направляющий вектор прямой
![]() и нормальный вектор плоскости α
и нормальный вектор плоскости α
![]() параллельны плоскости β
. Точка
параллельны плоскости β
. Точка
![]() и , если
и , если
![]() - текущая точка β
, то вектор
- текущая точка β
, то вектор
![]() лежит в плоскости β
. Векторы
лежит в плоскости β
. Векторы
![]() и
и
![]() -
компланарны . Запишем условие этого
-
компланарны . Запишем условие этого
![]()
![]() .
.
После
упрощения получаем β
:
![]() . Объединив это уравнение проектирующей
плоскости с уравнением плоскости
проекции α
, получим общие уравнения искомой
проекции q
прямой р :
. Объединив это уравнение проектирующей
плоскости с уравнением плоскости
проекции α
, получим общие уравнения искомой
проекции q
прямой р :
![]() (1)
(1)
Последний
шаг в решении задачи – переход от общих
уравнений (1) к каноническим, для чего
надо найти направляющий вектор прямой
q
и точку , ей принадлежащую (или две точки)
. Нормальные векторы плоскостей α
и β
, будучи перпендикулярными своим
плоскостям , перпендикулярны и линии
их пересечения q
. А значит их векторное произведение
параллельно q
,(по определению
![]() и
и
![]() т.е. может служить направляющим вектором
этой прямой:
т.е. может служить направляющим вектором
этой прямой:
![]() .
.
Чтобы найти точку , принадлежащую q , найдем какое-нибудь решение системы (1). Так как неизвестных больше уравнений , то одно из неизвестных , например z, можно выбрать произвольно . Пусть z = 0 . Тогда система (1) имеет вид
![]() .
.
Решив
ее , находим : x
= 1 , y
= 2 . Итак , теперь можно составить
канонические уравнения проекции q
прямой р на плоскость α
как прямой , проходящей через
![]() в направлении
в направлении
![]()
![]() .
.
Задача
10. Поворотом
системы координат исключить из уравнения
![]() член
, содержащий произведение переменных
.
член
, содержащий произведение переменных
.
Решение . Решим задачу в общем виде . Уравнение линии второго порядка имеет вид
![]() (2)
(2)
При
повороте системы координат на угол α
старые координаты точки (x,y)
связаны с новыми
![]() известными формулами
известными формулами
![]()
После подстановки этих формул в уравнение (2) и элементарных преобразований получим уравнение линии в новой системе координат :
![]() .
.
Здесь :
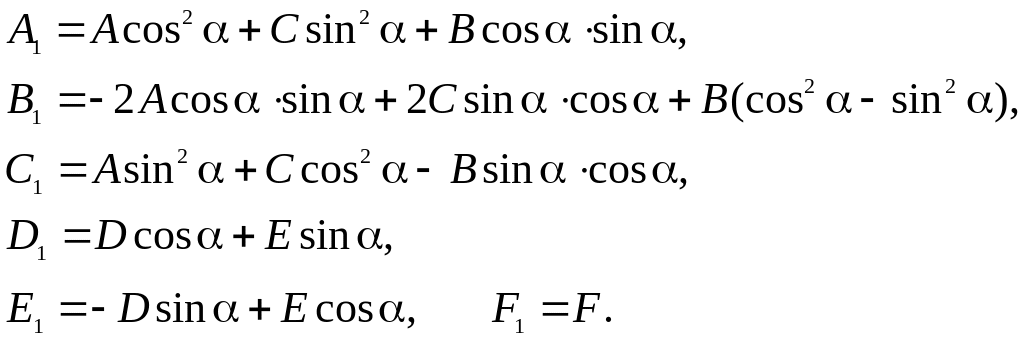
Если
мы хотим , чтобы пропал член , содержащий
произведение переменных , то угол α
необходимо выбрать таким , чтобы
![]() ,
т.е.
,
т.е.
![]() .
.
Итак, ответ в общем виде такой : угол поворота α должен удовлетворять уравнению
![]() .
.
В
нашей задаче имеем : А=5 , В=8, С=5 . Значит
![]() ,т.е.
,т.е.
![]() .
Одно из решений этого уравнения
.
Одно из решений этого уравнения
![]() .
Вычисляем новые коэффициенты по
приведенным выше формулам :
.
Вычисляем новые коэффициенты по
приведенным выше формулам :
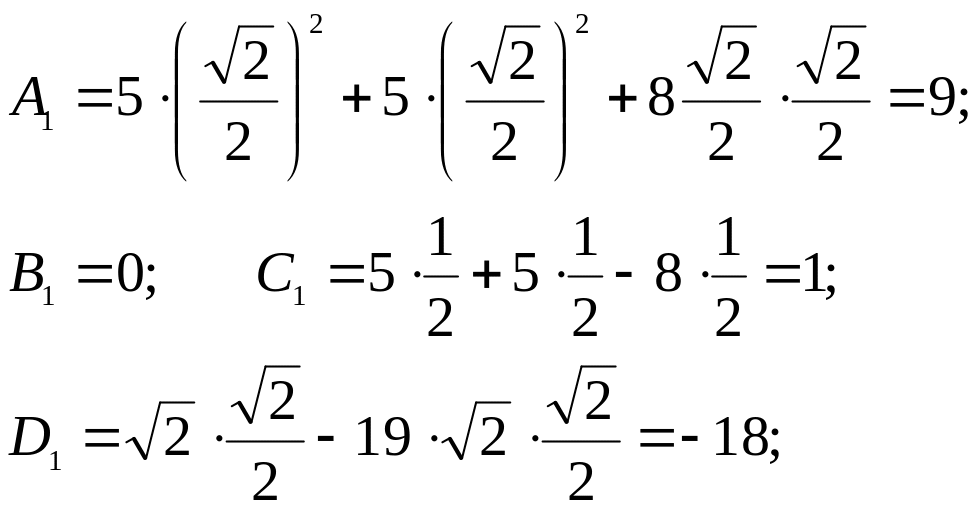
![]()
Итак
, повернув систему координат на
![]() , мы получим уравнение
, мы получим уравнение
![]() .
.
Замечание. Старшие коэффициенты полученного уравнения (не содержащего произведения переменных ! ) позволяют частично определить вид линии : т.к. эти коэффициенты имеют одинаковый знак , то данное уравнение определяет эллипс , или одну точку , или , вообще , ничего не определяют ( в последних двух случаях говорят, что уравнение определяет вырожденный или мнимый эллипс ) .
Ответ:
в новой системе координат линия имеет
уравнение
![]() .
.
Задача
11. Уравнение
линии
![]() привести к нормальному виду .
привести к нормальному виду .
Решение . Группируем одноименные переменные и выделяем в каждой группе полный квадрат :
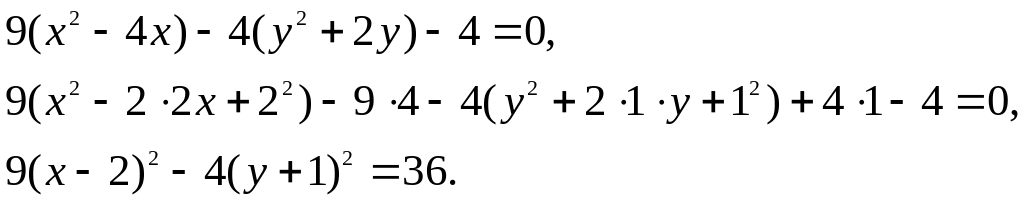
Разделив обе части последнего уравнения на правую часть , мы и получим нормальное уравнение линии :
![]() (3) .
(3) .
Это
уравнение определяет гиперболу , оси
которой параллельны осям координат
(это вытекает и из общего уравнения –
в нем отсутствует член , содержащий
![]() )
. Центр гиперболы расположен в точке
)
. Центр гиперболы расположен в точке
![]() ,
действительная полуось а=2
, мнимая b=3,
половина расстояния между фокусами
,
действительная полуось а=2
, мнимая b=3,
половина расстояния между фокусами
![]() .Вершины
:
.Вершины
:
![]() .Фокусы
:
.Фокусы
:
![]()
Гипербола
(3) получается из канонической гиперболы
![]() путем параллельного переноса центра в
точку
. Асимптоты канонической гиперболы
имеют уравнения
путем параллельного переноса центра в
точку
. Асимптоты канонической гиперболы
имеют уравнения
![]() , т.е.
, т.е.
![]() .
.
Для нашей гиперболы уравнения асимптот таковы
![]()
Ответ:
нормальное уравнение
![]()
Задача
12. Провести
касательную q
к линии : 1)
![]() , параллельную прямой
, параллельную прямой
![]() 2)
2)
![]() ,
перпендикулярную прямой
,
перпендикулярную прямой
![]() 3)
3)
![]() через точку М(-5;-4), принадлежащую линии;
4)
через точку М(-5;-4), принадлежащую линии;
4)
![]() через точку N(5;-7)
.
через точку N(5;-7)
.
Решение . Сделаем несколько общих замечаний относительно касательных к линиям второго порядка . Касательные к окружности , эллипсу , гиперболе и параболе можно определить как прямые , имеющие с линией единственную общую точку . Из этого определения надо сделать два исключения : прямые , параллельные оси параболы , и прямые ,параллельные одной из асимптот гиперболы . Эти прямые имеют с соответствующей линией одну общую точку , не являясь при этом касательными .
Если требуется провести касательную к линии через точку лежащую на ней , то можно использовать следующие свойства касательных : а) касательная к окружности перпендикулярна радиусу , проведенному в точку касания; b)касательная к эллипсу перпендикулярна биссектрисе угла , образованного фокальными радиусами точки касания ; с) касательная к гиперболе сама является биссектрисой этого угла ; d)касательная к параболе перпендикулярна биссектрисе угла , образованного осью параболы и фокальным радиусом точки касания .
1)В
качестве нормального вектора касательной
q
берем нормальный вектор данной прямой
![]() ,
а именно
,
а именно
![]() (т.к. по условию
(т.к. по условию
![]() )
. Уравнение касательной запишем в общем
виде
)
. Уравнение касательной запишем в общем
виде
![]() , а неизвестный параметр С определяем
из того условия , что q
и
, а неизвестный параметр С определяем
из того условия , что q
и
![]() имеют единственную общую точку . Другими
словами , система уравнений
имеют единственную общую точку . Другими
словами , система уравнений
![]()
должна иметь единственное решение. Выразим из первого уравнения y через x и подставим во второе уравнение. После преобразований получим
![]() .
.
Это квадратное уравнение имеет единственное решение (лучше , конечно , говорить о двух совпадающих решениях ) , если только его дискриминант равен 0 . Итак , для определения параметра С имеем условие
![]() .
.
Решая
его , находим :
![]() Итак , имеется две касательные к
Итак , имеется две касательные к
![]() , параллельные
.
Это
, параллельные
.
Это
![]() и
и
![]() .
.
2)Уравнение
прямой
![]() запишем в форме уравнения прямой с
угловым коэффициентом :
запишем в форме уравнения прямой с
угловым коэффициентом :
![]() . И уравнение касательной q
будем искать в такой же форме :
. И уравнение касательной q
будем искать в такой же форме :
![]() . А так как угловые коэффициенты
перпендикулярных прямых обратны по
величине и противоположны по знаку , то
k
=-2 . Неизвестный параметр b
находим , как и в предыдущем пункте , из
того условия , что система
. А так как угловые коэффициенты
перпендикулярных прямых обратны по
величине и противоположны по знаку , то
k
=-2 . Неизвестный параметр b
находим , как и в предыдущем пункте , из
того условия , что система
![]()
имеет
единственное решение . Другими словами
, дискриминант квадратного уравнения
![]() равен 0 . После преобразований получаем
уравнение для b
:
равен 0 . После преобразований получаем
уравнение для b
:
![]() .
.
Откуда
![]() .
Итак , имеется две касательных к
.
Итак , имеется две касательных к
![]() , перпендикулярные
:
, перпендикулярные
:
![]() ,
,
![]() .
.
3)Линия
![]() - это гипербола (старшие коэффициенты
противоположных знаков). Ее каноническое
уравнение
- это гипербола (старшие коэффициенты
противоположных знаков). Ее каноническое
уравнение
![]() .
.
Из
него находим :
![]() Ее
фокусы лежат на оси Ох (коэффициент
перед
Ее
фокусы лежат на оси Ох (коэффициент
перед
![]() положительный ) и имеют координаты
положительный ) и имеют координаты
![]() . Найдем векторы , направленные по
фокальным радиусам точки М(-5;-4) :
. Найдем векторы , направленные по
фокальным радиусам точки М(-5;-4) :
![]() и
и
![]() .
.
Теперь нетрудно найти вектор , направленный по биссектрисе угла , образованного фокальными радиусами точки М :
![]() .
.
Используя
свойство касательной к гиперболе , можно
сделать вывод : вектор
![]() является ее направляющим вектором .
Запишем уравнение касательной в
канонической форме :
является ее направляющим вектором .
Запишем уравнение касательной в
канонической форме :
![]() .
.
Итак , искомая касательная имеет вид
![]()
4)Уравнение
касательной будем искать в форме
![]() , где
, где
![]() , а k
– угловой коэффициент прямой q
. В нашем случае
, а k
– угловой коэффициент прямой q
. В нашем случае
![]() , а неизвестный параметр k
находим , как и в пунктах 1) и 2) , из того
условия , что система
, а неизвестный параметр k
находим , как и в пунктах 1) и 2) , из того
условия , что система
![]()
имеет единственное решение . После преобразований находим уравнение для ординат точек пересечения параболы и прямой :
![]() .
.
Дискриминант
этого уравнения приравняем к нулю и
получим уравнение для
![]() . Отсюда :
. Отсюда :
![]() Теперь
можно составить уравнения искомых
касательных :
Теперь
можно составить уравнения искомых
касательных :
![]() и
и
![]() .
.
Задача 13. Установить , какая линия определяется уравнением
![]() . (4)
. (4)
Решение . Уединим корень в правой части уравнения и возведем обе его части в квадрат :
![]() .
.
В уравнении имеется квадрат только одной переменной , значит оно определяет параболу . Приводим уравнение к нормальной форме :
![]() . (5)
. (5)
Эта
форма позволяет сказать о линии следующее
: вершина параболы находится в точке
V(-3;2)
, её ось – параллельна оси Оу , ветви
направлены вниз (знак ”-” перед правой
частью ) . Параметр параболы равен р=4 ,
поэтому фокус
![]() и директриса
и директриса
![]() .
.
Однако
, при возведении в квадрат обеих частей
исходного уравнения могли появиться
и появились посторонние решения . Так
как выражение
![]() всегда неотрицательно , то получаем ,
что абсциссы точек линии (4) удовлетворяют
условию
всегда неотрицательно , то получаем ,
что абсциссы точек линии (4) удовлетворяют
условию
![]() , то есть эта линия лежит левее прямой
, то есть эта линия лежит левее прямой
![]() .Итак , данное уравнение определяет
левую половину параболы (5) .
.Итак , данное уравнение определяет
левую половину параболы (5) .
Ответ:
уравнение
определяет восходящую ветвь параболы
![]() .
.
Какому условию должны удовлетворять векторы
 и
и
 ,
чтобы имело место указанное соотношение.
,
чтобы имело место указанное соотношение.
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() при
всяких значениях
при
всяких значениях
![]() и
и
![]() .
.
2.
Найти вектор
![]() ,
удовлетворяющий указанным условиям.
,
удовлетворяющий указанным условиям.
![]()
![]()
![]()
![]()
![]()
![]() где
где
![]()
![]()
![]()
![]()
![]()
![]() где
где
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() где
где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.1 - 18. Выполнить указанные действия над векторами, заданными в различных формах.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.19
– 25. Найти проекцию вектора
![]() на направление вектора
на направление вектора
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. Треугольник ACD задан координатами своих вершин. В каждой задаче, кроме указанного в условии, вычислить площадь треугольника, не находя длины его сторон. Принятые обозначения: точки B, H и M – точки пересечения биссектрис, высот и медиан треугольника соответственно; BA – биссектриса угла при вершине A; HC – высота, опущенная из вершины C на противоположную сторону; MD – медиана проведенная из вершины D. Сделать чертеж.
4.1 A(3;-5), C(-1;-2), D(-3;3). Найти: 1) уравнение и длину BA; 2) уравнение MC;3) угол между BA и HC.
4.2 A(2;8), C(6;4), D(-4;2). Найти: 1) уравнение и длину MA; 2) уравнение HA;3) угол между BA и MA.
4.3 A(0;5), C(-3;4), D(5;0). Найти: 1) уравнение и длину MA; 2) точку H; 3)угол между MA и HA.
4.4 A(-8;2), C(2;2), D(10;8). Найти: 1) уравнение и длину BC; 2) точку H; 3)угол между HD и MC.
4.5 A(-2;-3), C(6;-6), D(2;3). Найти: 1) уравнение и длину HD; 2) точку M; 3) угол между MD и MA.
4.6 A(4;-4), C(0;1), D(-2;4). Найти: 1) уравнение и длину HD; 2) уравнение BA;3) угол между HD и BA.
4.7 A(-3;-8), C(9;0) D(3;8). Найти: 1) уравнение и длину BD; 2) точку M; 3)угол между BD и MD.
4.8 A(0;10), C(4;6) D(-6;4). Найти: 1) уравнение и длину MD; 2) центр описанной окружности и ее радиус; 3) углы треугольника.
4.9 A(1;7), C(-2;-2) D(6;2). Найти: 1) уравнение AK║CD; 2) точку H; 3) угол между HC и MA.
4.10 A(8;6), C(2;0) D(6;8). Найти: 1) уравнение и длину HC; 2) уравнение KL, где K и L – середины сторон CD и CA; 3) угол ACM.
4.11 A(8;14), C(16;-2) D(2;-4). Найти: 1) уравнение и длину MD; 2) центр описанной окружности и ее радиус; 3) угол между HA и MD.
4.12 A(4;2), C(6;-12) D(18;0). Найти: 1) уравнение и длину MA; 2) центр вписанной окружности и ее радиус; 3) угол CBA.
4.13 A(-7;-3), C(1;9) D(9;3). Найти: 1) уравнение и длину HC; 2) точку M; 3)угол между HC и MA.
4.14 A(-5;-1), C(5;-1) D(13;5). Найти: 1) уравнение и длину MС; 2) точку H; 3) угол между BC и HD.
4.15 A(1;-2), C(-2;0) D(5;6). Найти: 1) уравнение и длину BA; 2) центр описанной окружности и ее радиус; 3) уравнение HA.
4.16 A(2;14), C(-4;-4) D(12;4). Найти: 1) уравнение и длину PQ, где P и Q – середины сторон AC и AD; 2) точку H; 3) угол между MA и HA.
4.17 A(-6;-13), C(12;-7) D(4;17). Найти: 1)уравнение и длину HC; 2)точку B; 3) угол между MC и HC.
4.18 A(2;-8), C(2;2) D(8;10). Найти: 1) уравнение и длину HC; 2) центр описанной окружности и ее радиус; 3) угол DMC.
4.19 A(0;-1), C(4;5) D(8;-4). Найти: 1) уравнение DK║AC; 2) точку M; 3)угол между HD и MD.
4.20 A(0;4), C(2;-10) D(14;2). Найти: 1) уравнение CD; 2) центр вписанной окружности и ее радиус; 3) угол между HC и MA.
4.21 A(4;5), C(-3;-1) D(0;-3). Найти: 1) уравнение и длину BD; 2) уравнение AK║CD; 3) углы треугольника.
4.22 A(3;0), C(-3;2), D(3;8). Найти: 1) уравнение и длину HA; 2) центр описанной окружности и ее радиус; 3) угол между HA и MC.
4.23 A(-2;1), C(6;-5) D(-2;11). Найти: 1) уравнение и длину BA; 2) точку H; 3) угол MAC.
4.24 A(2;4), C(-12;6) D(0;18). Найти: 1) уравнение и длину HA; 2) точку B; 3) расстояние от B до стороны AD.
4.25 A(2;-6), C(-2;-3) D(-4;2). Найти: 1) уравнение и длину MC; 2)уравнение HD;3)угол между HD и MC.
5.Установить, какую линию определяет уравнение, определить фокусы, вершины, оси линии, нарисовать ее.
5.1. 4x2 – y2 –8x – 4y – 4 = 0.
x2 + y2 –2x – 4y + 1 = 0.
4y2 – 8x – 4y + 9 = 0.
x2 – 4y2 + 8y + 4 = 0.
x2 + 2x + 4y – 7 = 0.
4x2 + 4y2 – 8x – 24y + 31 = 0.
x2 + 4y2 + 4x – 8y + 4 = 0.
x2 – y2 – 6x – 4y + 1 = 0.
y2 + 8x – 6y + 25 = 0.
x2 + y2 + 8x + 2y + 1 = 0.
4x2 + y2 – 8x + 4y + 4 = 0.
4x2 – y2 – 8x – 6y – 9 = 0.
y2- 16x + 6y + 25 = 0.
2x2 + 2y2 + 16x – 28y + 53 = 0.
x2 + 9y2 –2x +18y + 1 = 0.
x2 – 4y2 – 8x +8y + 16 = 0.
x2 – 4x – 4y + 12 = 0.
x2 + y2 – 8x + 2y + 16 = 0.
9x2 + 4y2 – 18x + 24y + 9 = 0.
x2 – 9y2 – 8x + 18y – 2 = 0.
3x2 + 3y2 – 42x + 6y + 146 = 0.
y2 + 10x – 10y + 55 = 0.
9x2 – 16y2 – 36x + 32y + 164 = 0.
y2 – 20x – 14y + 37 = 0.
9x2 + 16y2 – 18x + 96y + 9 = 0.
6.Установить , какая линия определяется уравнением , нарисовать ее.
6.1. ![]() 6.2.
6.2. ![]()
6.3. ![]() 6.4.
6.4. ![]()
6.5. ![]() 6.6.
6.6. ![]()
6.7. ![]() 6.8.
6.8. ![]()
6.9. ![]() 6.10.
6.10. ![]()
6.11. ![]() 6.12.
6.12. ![]()
6.13. ![]() 6.14.
6.14. ![]()
6.15. ![]() 6.16.
6.16. ![]()
6.17. ![]() 6.18.
6.18. ![]()
6.19. ![]() 6.20.
6.20. ![]()
6.21. ![]() 6.22.
6.22. ![]()
6.23. ![]() 6.24.
6.24.![]()
6.25. ![]()
7.1-8.Провести касательные к линии l , параллельные прямой p.
7.1. l: ![]() , p: 2x+y-7=0.
, p: 2x+y-7=0.
7.2. l: ![]() , p: 4x-2y+23=0.
, p: 4x-2y+23=0.
7.3. l: ![]() , p: 10x-3y+9=0.
, p: 10x-3y+9=0.
7.4. l: ![]() , p: 3x-2y+13=0.
, p: 3x-2y+13=0.
7.5. l: ![]() , p: 3x-4y+7=0.
, p: 3x-4y+7=0.
7.6. l: ![]() , p: 2x+2y-13=0.
, p: 2x+2y-13=0.
7.7. l: ![]() , p: x-y-7=0.
, p: x-y-7=0.
7.8. l: ![]() , p: 2x-y+3=0.
, p: 2x-y+3=0.
7.9-16.Провести касательные к линии l , перпендикулярные прямой p.
7.9. l: ![]() , p: x-2y+9=0.
, p: x-2y+9=0.
7.10. l: ![]() , p: 2x-2y-5=0.
, p: 2x-2y-5=0.
7.11. l: ![]() , p: 4x+3y-7=0.
, p: 4x+3y-7=0.
7.12. l: ![]() , p: 4x+2y-1=0.
, p: 4x+2y-1=0.
7.13. l: ![]() , p: y-2x-4=0.
, p: y-2x-4=0.
7.14. l: ![]() , p: 3x-2y-6=0.
, p: 3x-2y-6=0.
7.15. l: ![]() , p: 5x+2y+8=0.
, p: 5x+2y+8=0.
7.16. l: ![]() , p: x+y-17=0.
, p: x+y-17=0.
7.17-21.Через точку М провести касательную к линии l .
7.17. M(-9;3), l: ![]() .
.
7.18. M(
2;2), l: ![]() .
.
7.19. M(0;-6), l: ![]() .
.
7.20. M(0;11), l: ![]() .
.
7.21. M(
7;0), l: ![]() .
.
7.22-25.Вывести условие, при котором прямая y=kx+b касается линии l .
7.22. l
: ![]() .
.
7.23. l
: ![]() .
.
7.24. l
: ![]() .
.
7.25. l
: ![]() .
.
8. Определить параметры, входящие в уравнения прямых и плоскостей, используя данные об их взаимном расположении.
8.1
![]()
![]()
![]()
![]()
![]()
8.2
![]()
![]()
![]()
![]()
8.3
![]()
![]()
![]()
8.4
![]()
![]()
![]()
8.5
![]()
![]()
![]()
![]()
![]()
8.6
![]()
![]()
8.7
![]()
![]()
8.8
![]()
![]()
![]()
8.9
![]()
![]()
8.10
![]()
![]()
8.11
![]()
![]()
8.12
![]()
![]() )
)
8.13
![]()
![]()
8.14
![]()
![]()
8.15
![]()
![]()
8.16
![]()
![]()
8.17
![]()
![]()
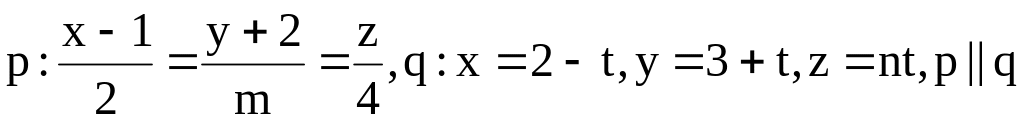
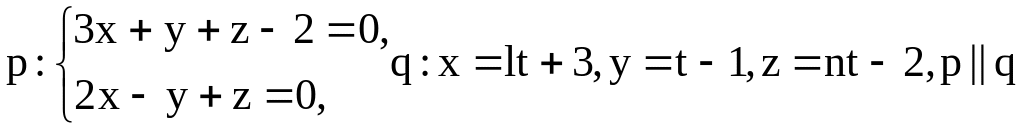

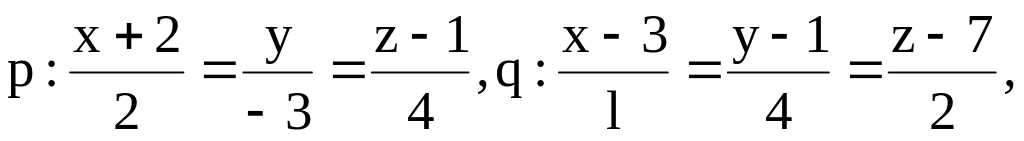
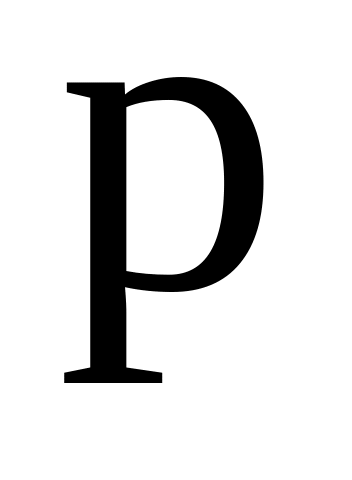

 -
пересекаются
-
пересекаются p
и q
– пересекаются
p
и q
– пересекаются p
и q
– пересекаются
p
и q
– пересекаются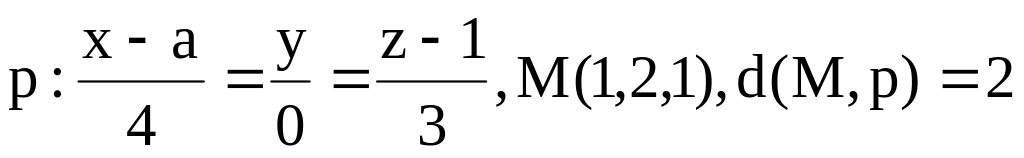
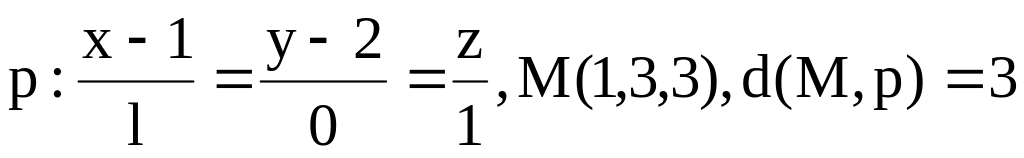
9.
Составить уравнение плоскости
![]() и найти расстояние точки N
от неё. Выяснить, лежат ли точка N
и начало координат по одну или по разные
стороны относительно плоскости
и найти расстояние точки N
от неё. Выяснить, лежат ли точка N
и начало координат по одну или по разные
стороны относительно плоскости
![]() .
.
9.1
А![]() .
.
9.2
![]() .
.
9.3
![]() .
.
9.4
![]() линии
пересечения плоскостей
линии
пересечения плоскостей
![]() .
.
9.5
![]() .
.
9.6
![]() .
.
9.7
![]() .
.
9.8
![]() .
.
9.9
![]() .
.
9.10
![]() проходит через линию пересечения
плоскостей
проходит через линию пересечения
плоскостей
![]() .
.
9.11
![]() .
.
9.12
![]()
![]() .
.
9.13
![]() .
.
9.14
![]() .
.
9.15
![]() .
.
9.16
![]() .
.
9.17
![]() .
.
9.18
![]() .
.
9.19
![]() .
.
9.20
![]() .
.
9.21
![]() .
.
9.22
![]() .
.
9.23
![]() .
.
9.24
![]() .
.
9.25
![]()
10.Составить канонические, параметрические или общие уравнения прямой р,проходящей через точку N, используя данные о расположении p относительно других объектов.
N (-1,2,-3) , p|| q:
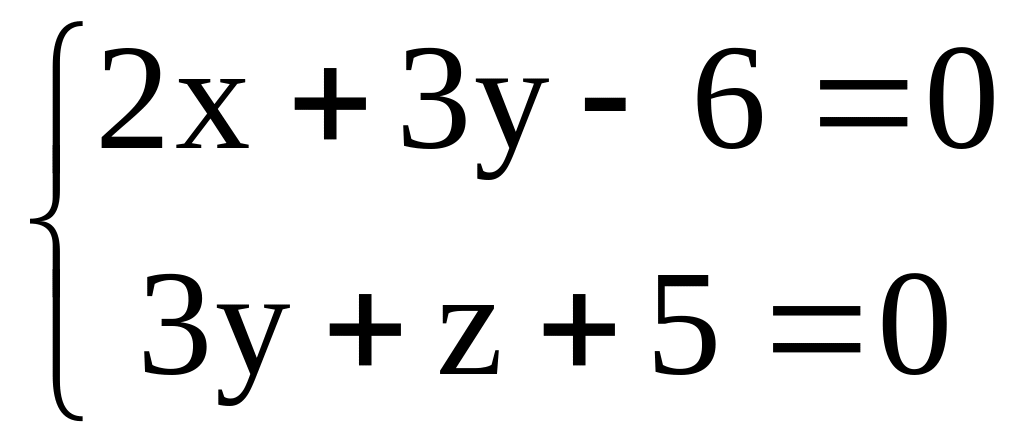 .
.N (2,2,5) , p
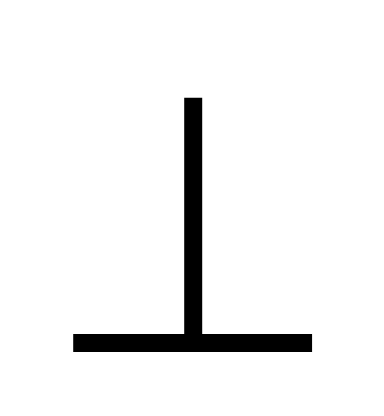
 ={1,2,0},
={1,2,0},
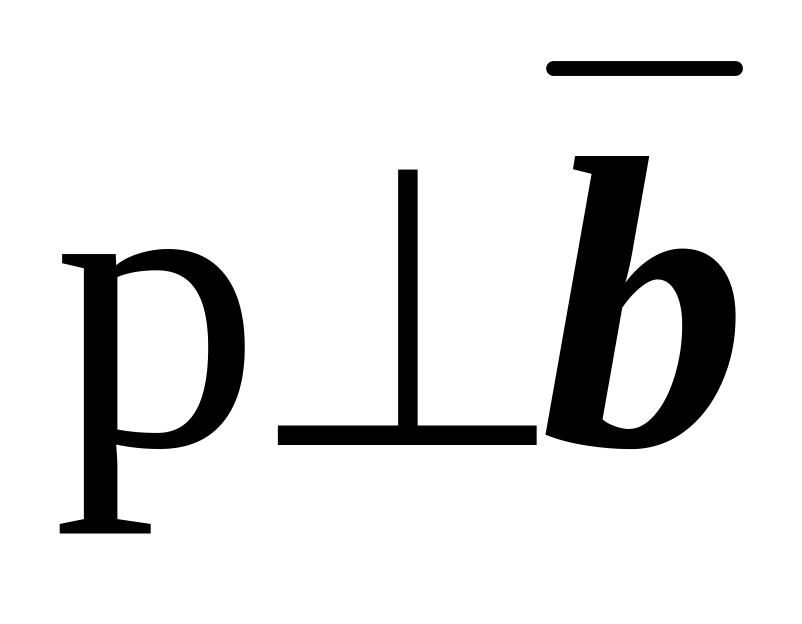 ={0,3,7}.
={0,3,7}.N (1,0,5) , p|| : 3x-y+7z=0 , p пересекается с прямой
q: ![]() =
=![]() =
=![]()
N (2,-3,1) , p ={2,1,-1} , p пересекается с прямой q:
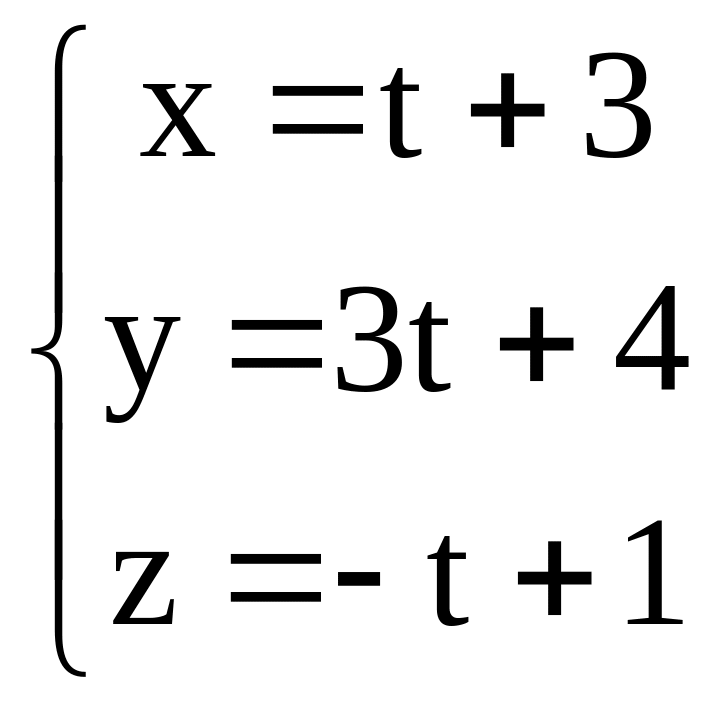 .
.N (3,1,0) , p|| : x-3y+z-1=0 , p||
 :
2x+3y+z+3=0.
:
2x+3y+z+3=0.N (4,-3,1) , p|| : x+2y-3z-1=0 , p пересекается с прямой
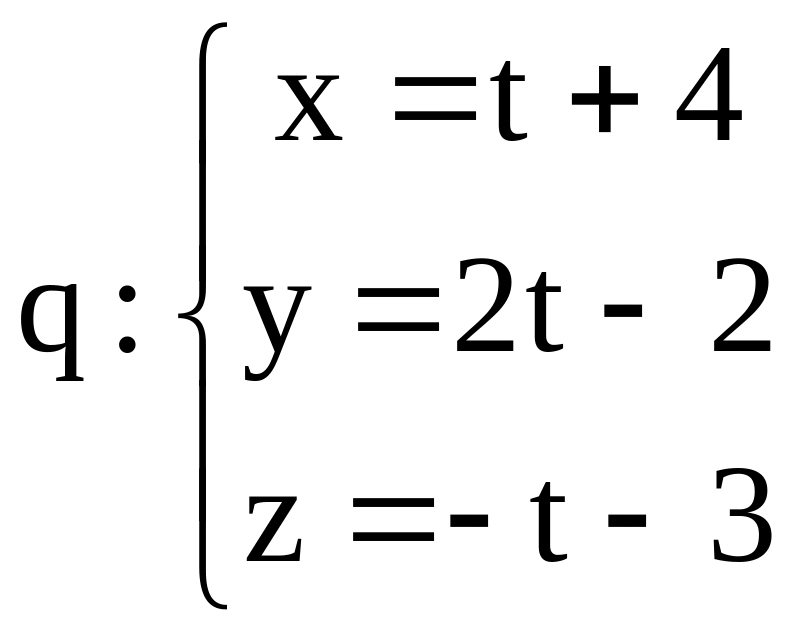 .
.N (5,7,-5) , p q:
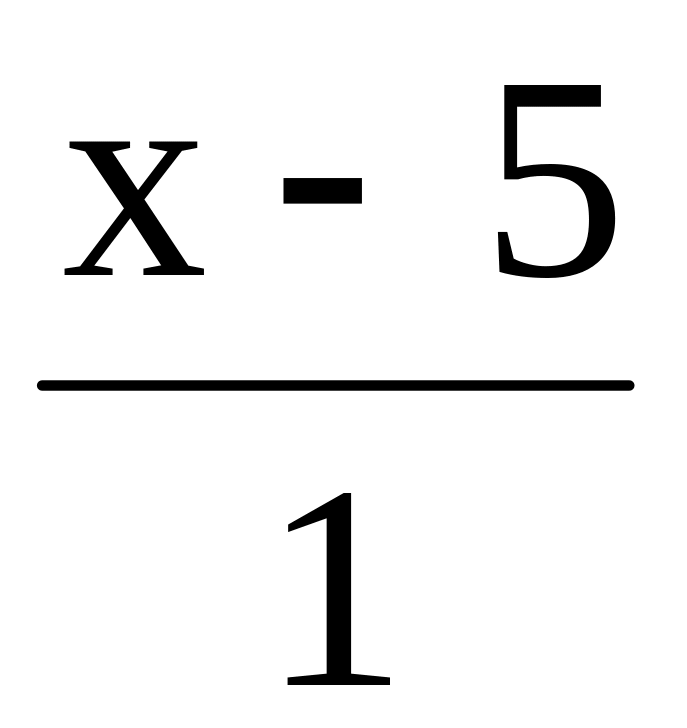 =
=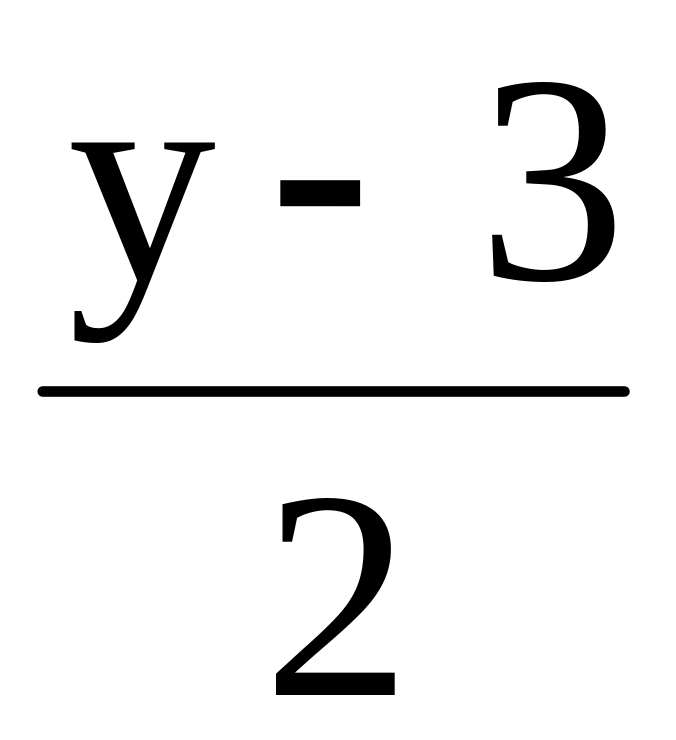 =
=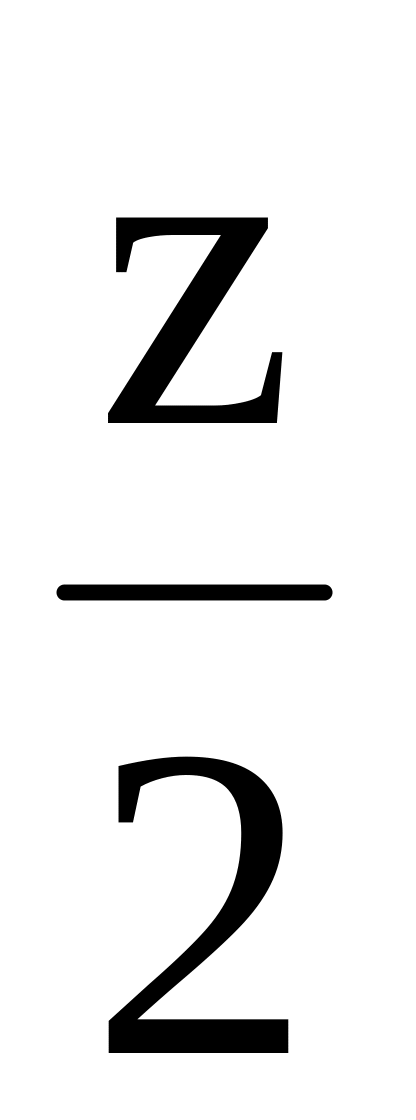 , p
и q
– пересекаются.
, p
и q
– пересекаются.N (3,2,-2) , p пересекается с прямыми q:
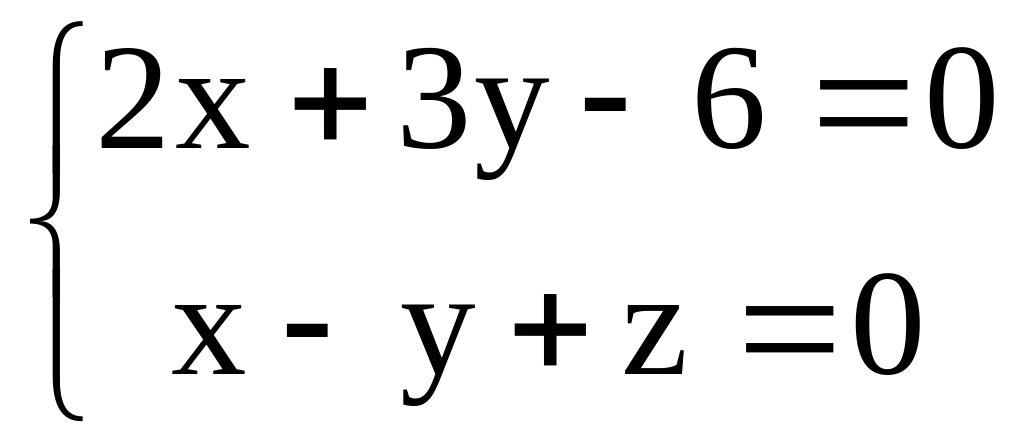 и r:
и r: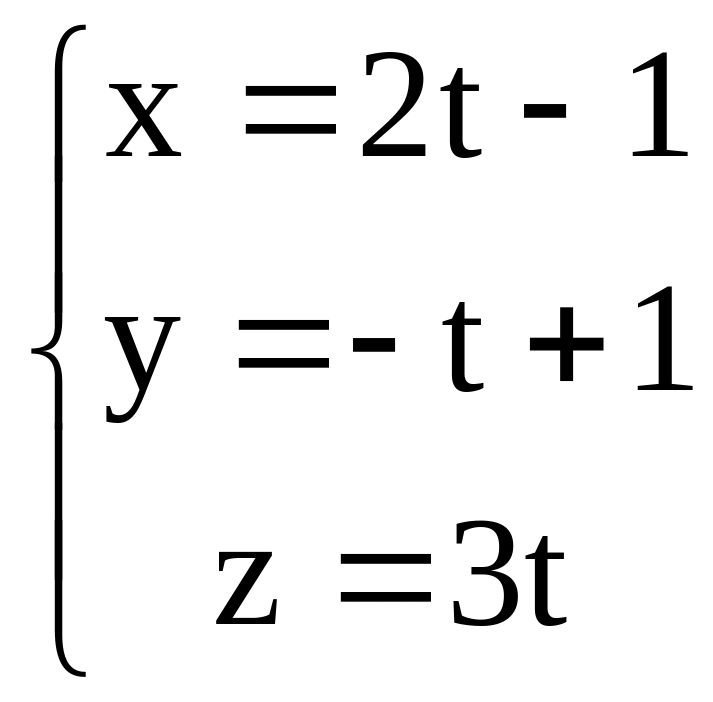 .
.N (4,1,-3) , p
 ={3,-2,1}
, p
пересекается с прямой
q:
={3,-2,1}
, p
пересекается с прямой
q:
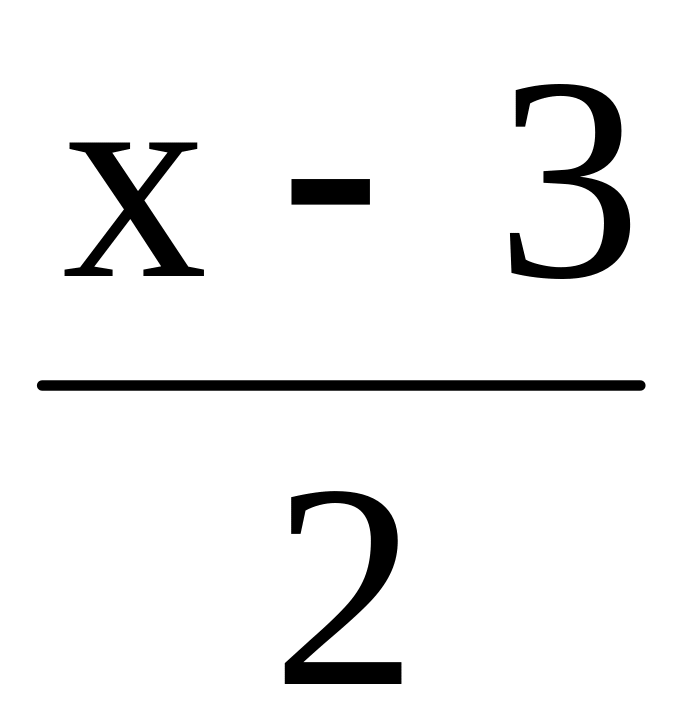 =
=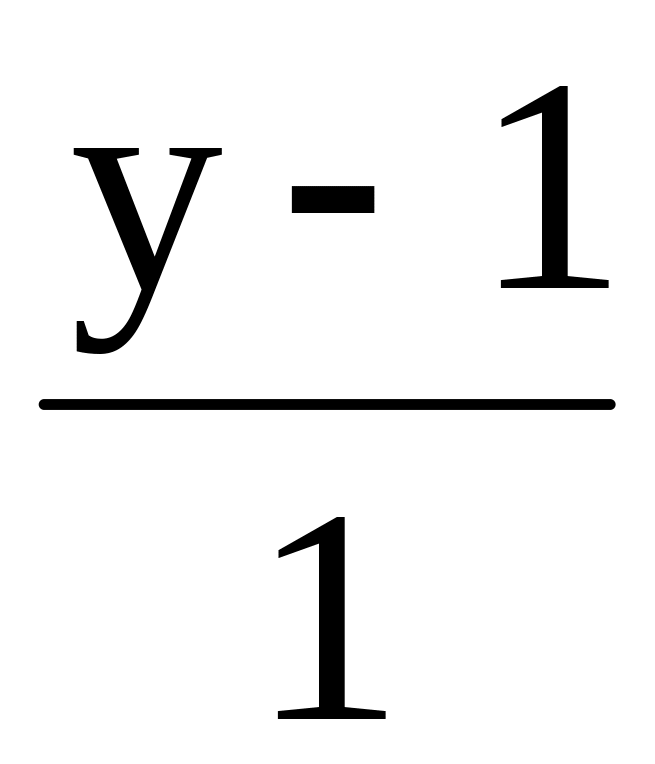 =
=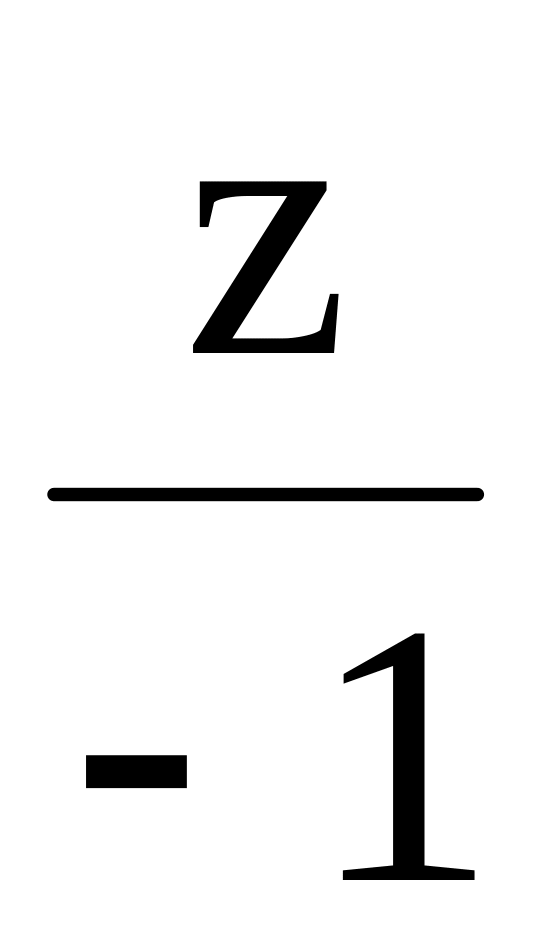 .
.N (5,7,3) , p пересекается с прямой q:
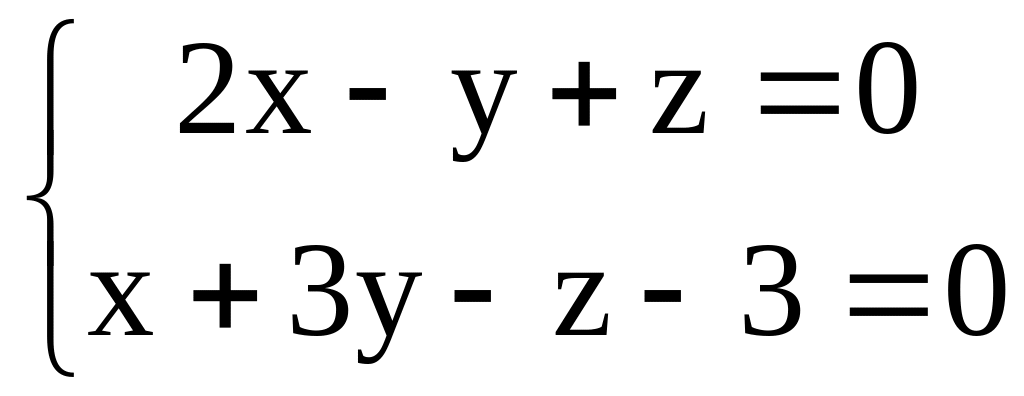 и
p
q.
и
p
q.N (7,1,1) , p ={3,4,-1} , p|| : 2x-3z+6=0.
N (-2,3,1) , p
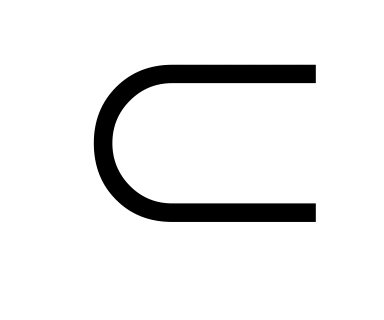 :
3x+y+3=0 , p||
:
2y-z+1=0.
:
3x+y+3=0 , p||
:
2y-z+1=0.N (4,2,1) , p
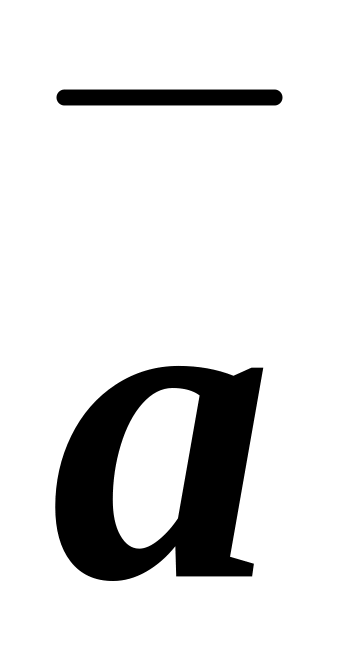 ={7,1,2}
, p
q:
={7,1,2}
, p
q:
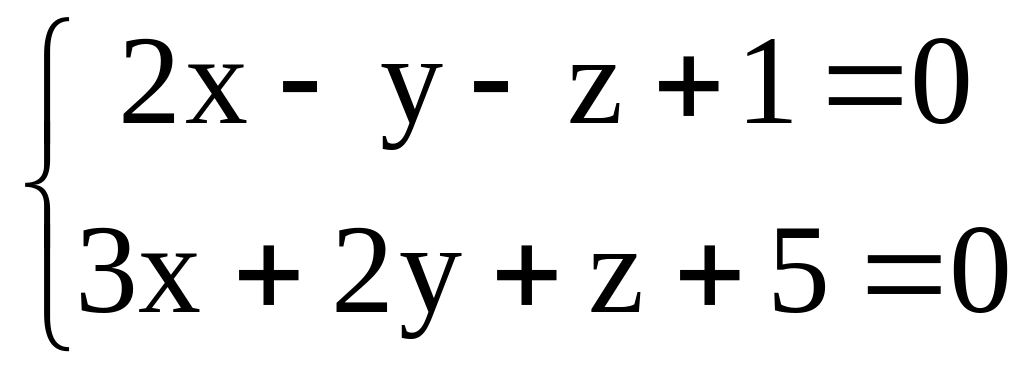 .
.N (2,3,2) , p
 :
3x-2y+z-2=0 , p
:
3x-2y+z-2=0 , p ={2,0,1}.
={2,0,1}.N (-3,-,5) , p|| :2x-3y-z+1=0 , p q:
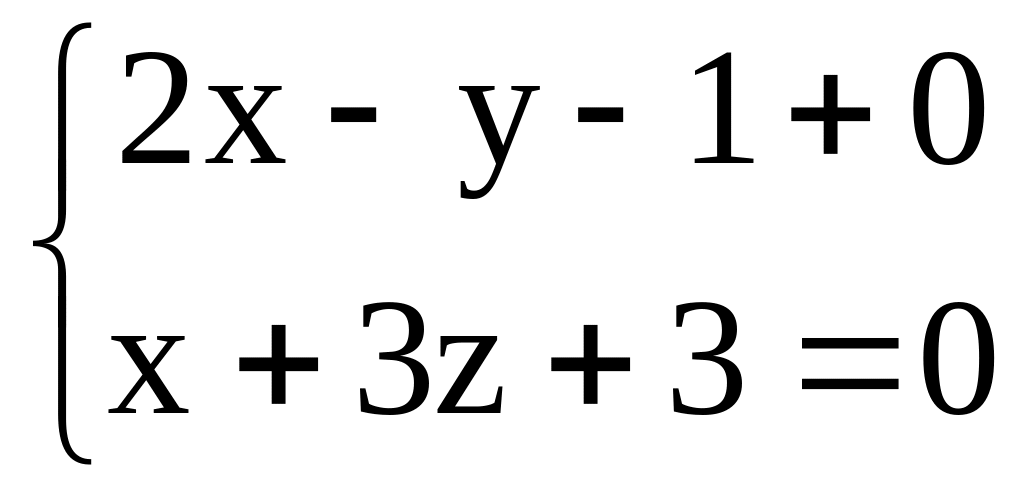 .
.N (1,7,9) , p q:
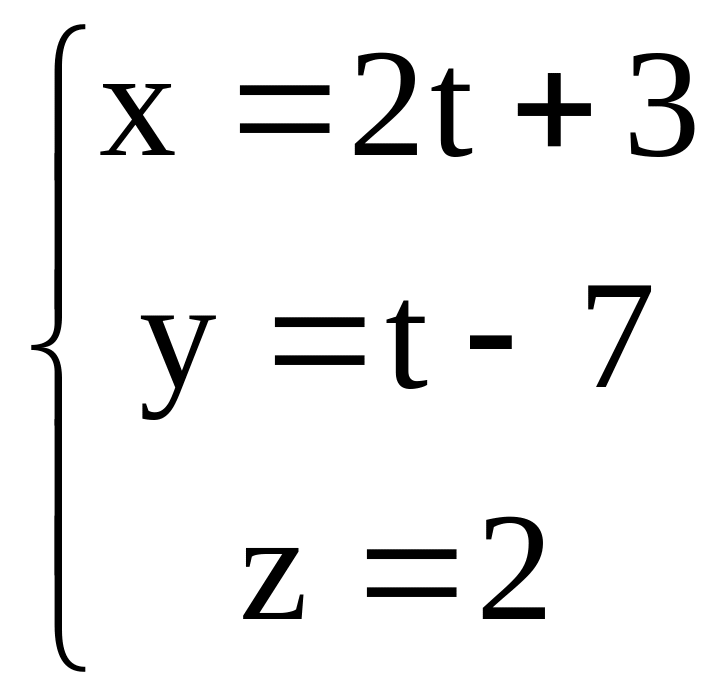 , p
и q
–пересекаются.
, p
и q
–пересекаются.N (2,-3,-5) , p
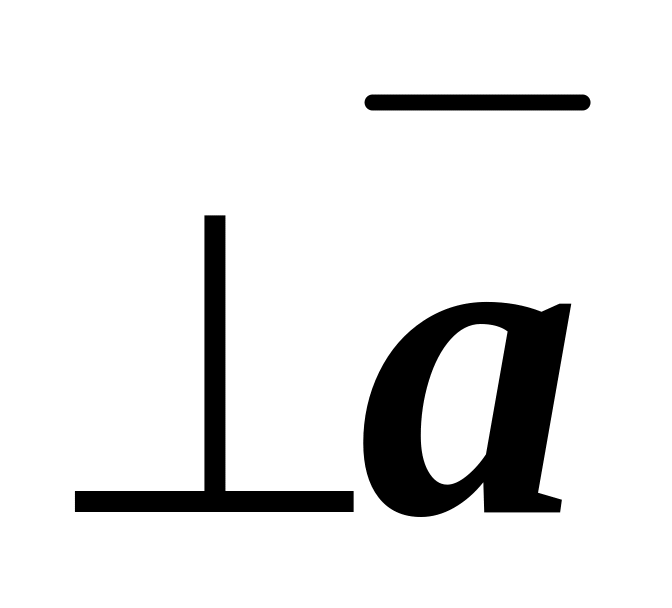 ={2,-1,-3}
, p
q:
={2,-1,-3}
, p
q:
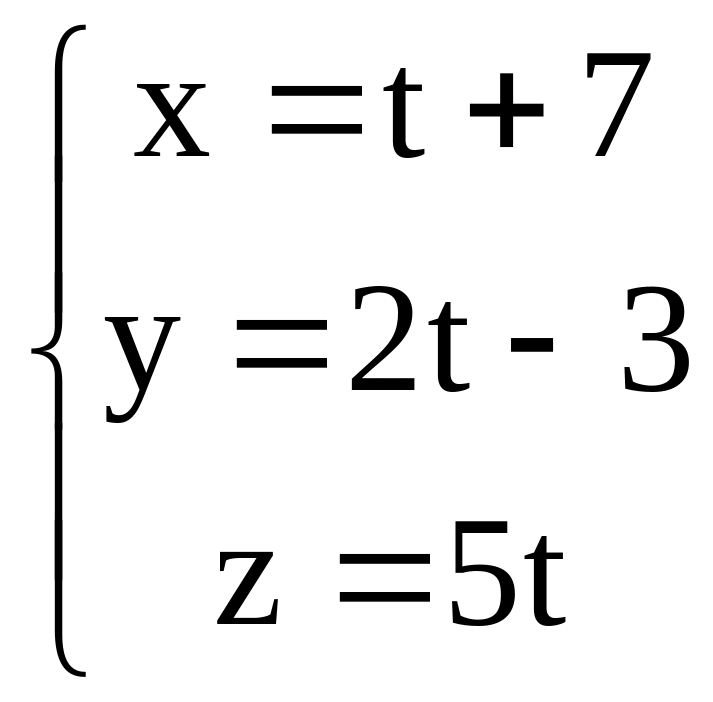 .
.
10.18
N
(7,-3,1) , p
={1,-1,2}
, p
пересекается с прямой q:![]() .
.
10.19
N
(-1,2,1) , p![]() ={3,5,1}
, p
={3,5,1}
, p
![]() ={1,2,2}.
={1,2,2}.
10.20
N
(6,3,7) , p![]() :3x-y+z-2=0
, p
q:
:3x-y+z-2=0
, p
q:![]() =
=![]() =
=![]() .
.
N (4,2,2) , p q:
 ,
p
r:
,
p
r: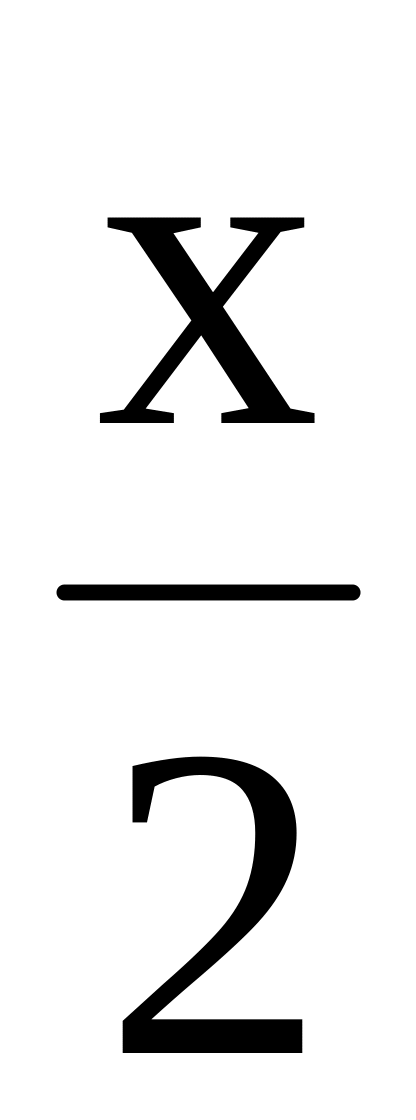 =
=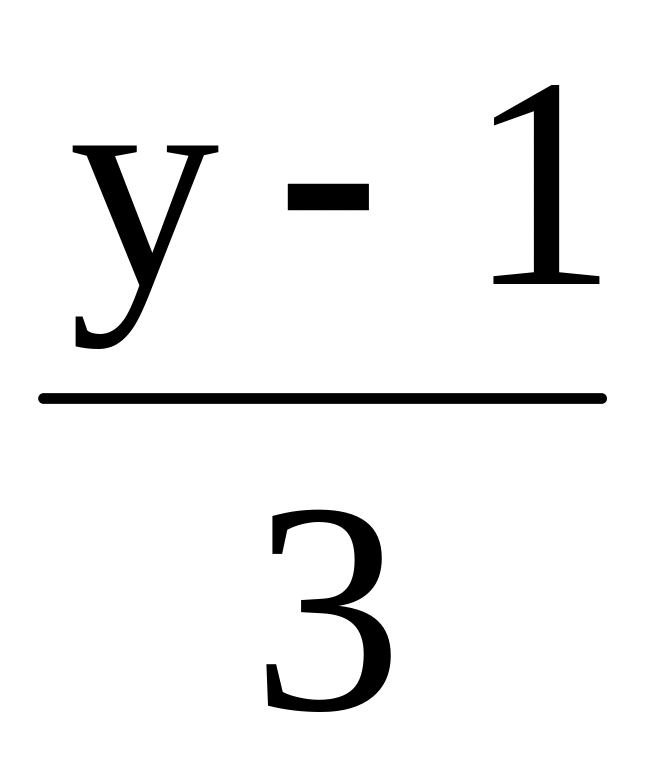 =
=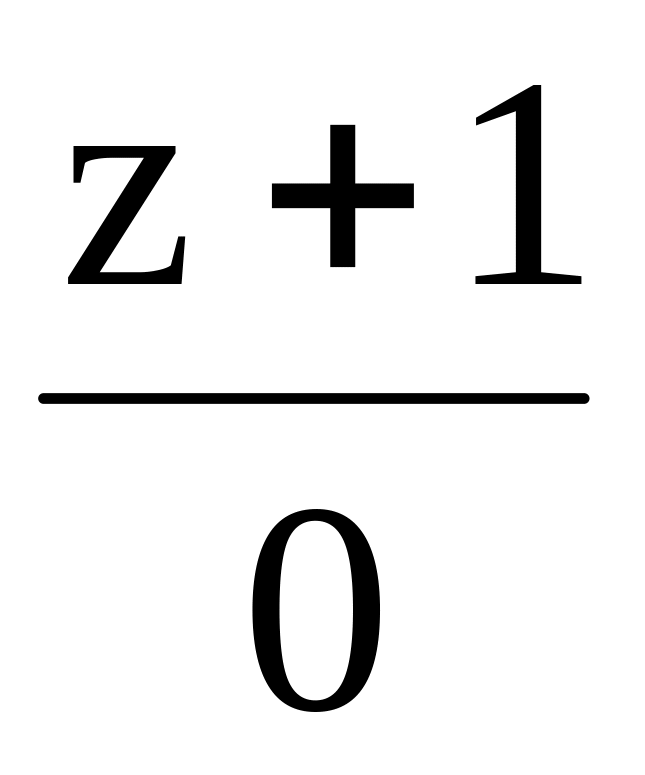 .
.N (1,1,3) , p|| :2x-3y-z=0 , p q:
 .
.N (5,0,1) , p|| :x-3y+z=0 , p|| :2x+3z-1=0.
N=q
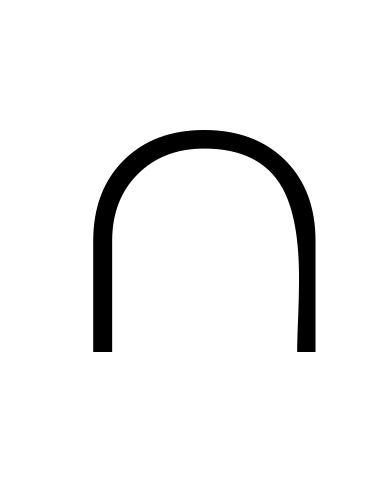 , где q:
=
=
, где q:
=
=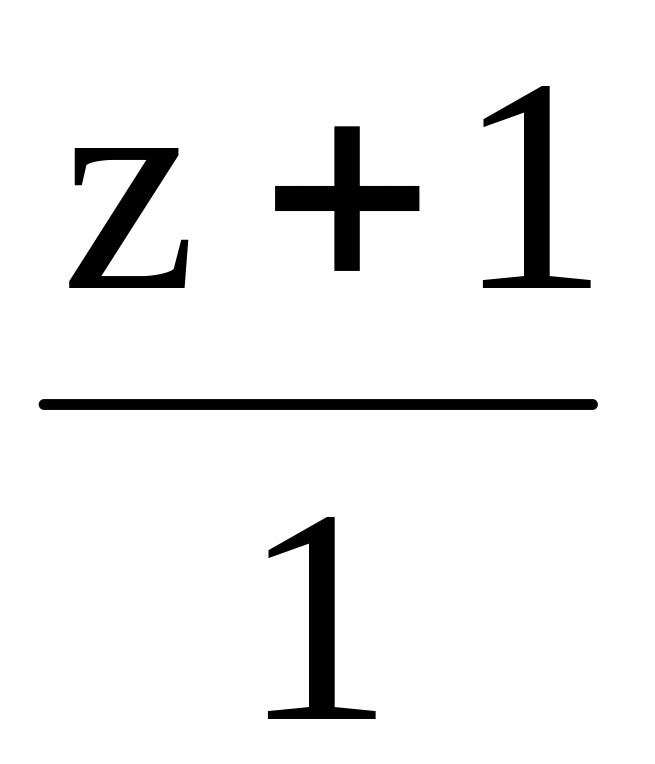 ,
:2x+7y-z+0
,p|| r:
,
:2x+7y-z+0
,p|| r: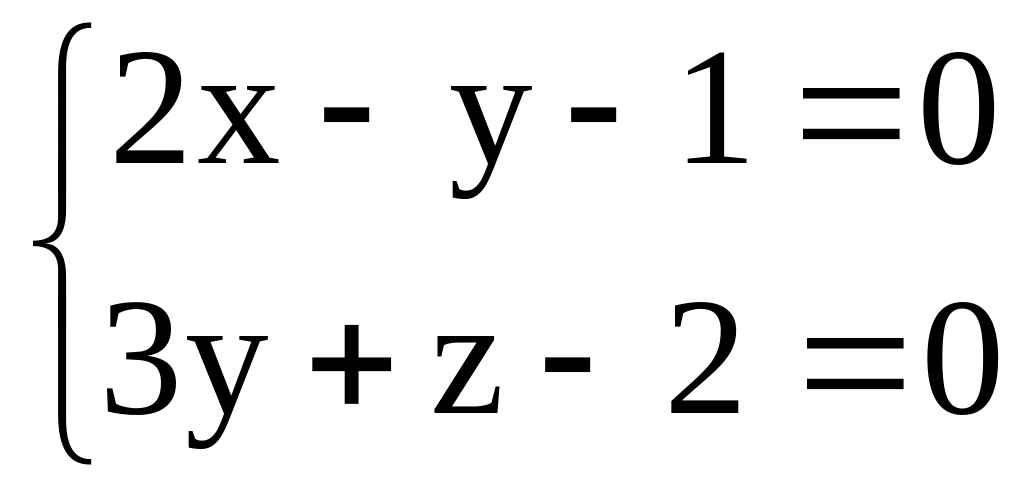 .
.N=q
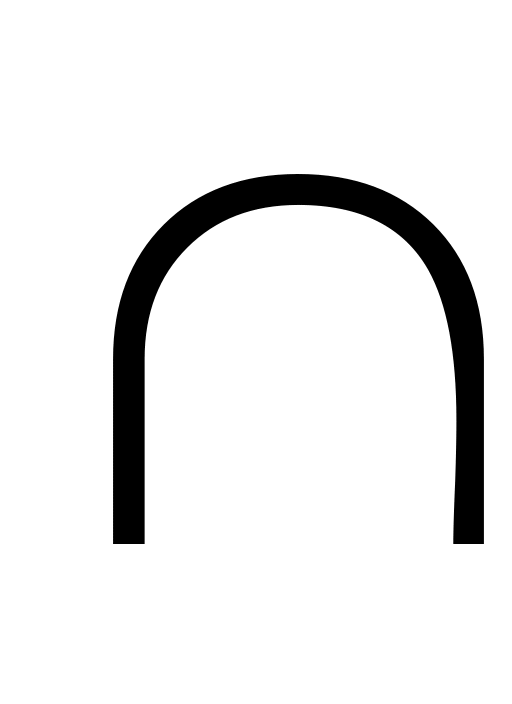 , где,
, где,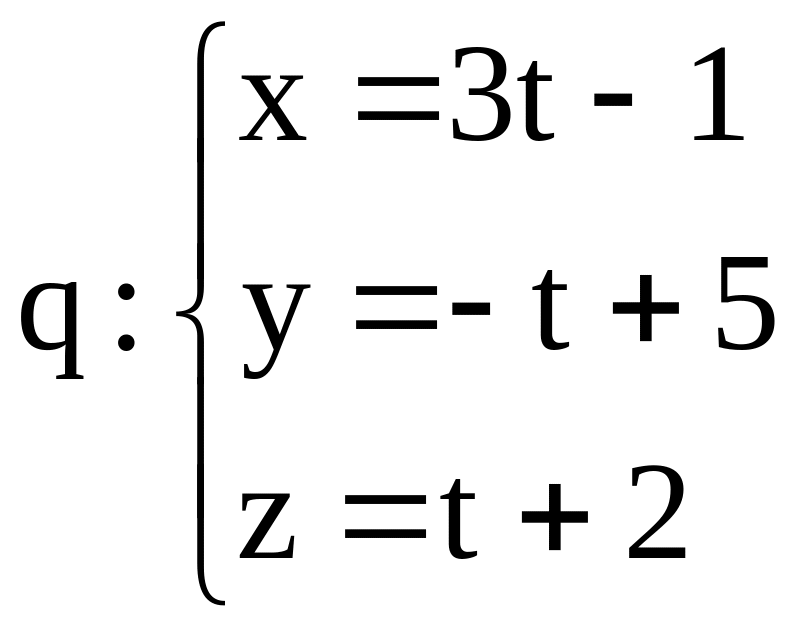 :
x+2y+z-13=0
, p
:
x+2y+z-13=0
, p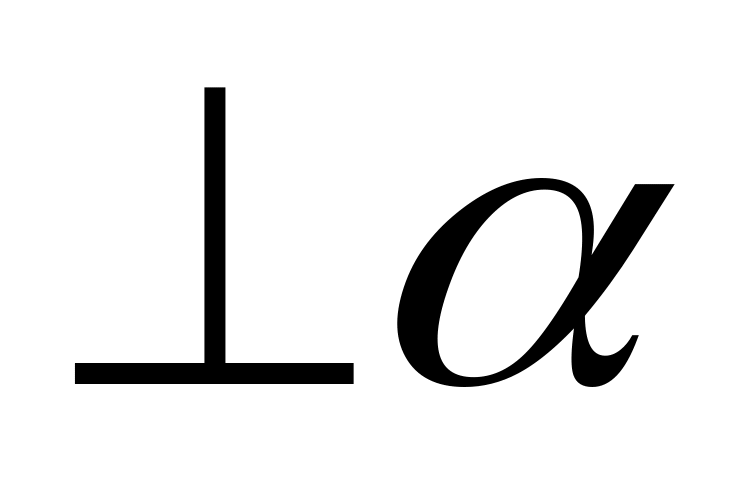 .
.
11. Найти угол между прямой р из задачи 10 и плоскостью из задачи 9.
12.1-4. Найти проекцию точки М на прямую р или плоскость .
![]()
![]()
![]()
![]()
12.5-7.Найти расстояние от точки M до прямой p.
![]()
![]()
![]()
12.8-11.Найти точку N , симметричную точке М относительно плоскости или прямой р .
![]()
![]()
![]()
![]()
12.12-15.Не находя точку пересечения , доказать , что прямые p и q пересекаются.
![]()
![]()
![]()
![]()
12.16-18.Составить уравнение плоскости ,проходящей через прямую р и параллельную прямой q.
![]()
![]()
![]()
12.19-22.Найти расстояние между прямыми p и q .
![]()
![]()
![]()
![]()
12.23-25.Составить каноническое уравнение проекции прямой р на плоскость .
![]()
![]()
![]()
Список рекомендованной литературы
1.Ильин В.А., Позняк Э.Г. Аналитическая геометрия . –М.: Наука . –223с.
2.Пак В.В., Носенко Ю.Л. Вища математика : Підручник . –К.: Либідь, 1996. –440с.
3.Клетеник Д.В. Сборник задач по аналитической геометрии. - СПб.: Спец. лит.,1998. –200с.
4.Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. –М.: Наука , 1970. –336с.
5.Сборник задач по математике для ВТУЗов . Линейная алгебра и основы математического анализа . / Под ред. Ефимова А.В., Демидовича Б.П. – М.:Наука,1986. -462 с.
6.Кузнецов Л.А. Сборник заданий по высшей математике . –М.: Высш.шк., 1983. –175с.
7.Ефимов Н.В. Краткий курс аналитической геометрии . –М. : Наука , 1975. –272с.
Содержание
