Контрольная 1

Задание

Задание согласно варианта представлено в таблице 1.

Номер ветви	Начало - конец	Сопротивления, Ом	Источники
			ЭДС, В	тока, А
1	61	540	0	0
2	13	420	0	1
3	32	230	0	0
4	24	310	0	0
5	45	160	0	0
6	56	610	200	0
7	36	130	0	0
8	14	320	300	6

Определить токи и напряжение U₅₁. Составить баланс мощностей. Методом эквивалентного генератора определить ток в ветви R₁.

Решение.

Изобразим граф схемы

Рис. 1. Граф схемы

Включим ветви цепи сопротивления и источники ЭДС. Источники тока подключаем параллельно соответствующим ветвям (рисунок 2).

Расчёт токов методом контурных токов

На рисунке 2обозначим направления контурных токов.

Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на (n-1).Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока - контурного тока, являющегося расчётной величиной.

Считаем, что в каждом независимом контуре течёт свой контурный ток: I_I, I_II, I_III. Составим уравнения по второму закону Кирхгофа относительно контурных токов:

Рис. 2. Схема цепи

или

Подставим в систему уравнений числовые значения:

Полученную систему решим методом Крамера. Вычислим определитель системы:

 = = 1.357·10⁹.

Вычислим три дополнительные определители системы, полученные из определителя системы заменой одного из его столбцов свободными членами:

₁ = =-3.786·10⁸.

₂ = = -1.640·10⁹.

₃ = = 1.567·10⁹.

Контурные токи равны:

Найдём токи в ветвях цепи:

I₁ = I_III- I_I = 1.434 (А),

I₂ = I_I - I_II + J₀₂ = 1.930 (А),

I₃ =- I_II = 1.209 (А),

I₄ =I₃ = 1.209 (А),

I₅ =I_III = 1.155 (А),

I₆ =I₅ = 1.155 (А),

I₇ =- I_I= 0.279 (А),

I₈ = I_II - I_III + J₀₈ = 3.636 (А).

Определение напряжения U₅₁

Для определения напряжения U₅₁ воспользуемся рисунком 2. Примем условно потенциал точки 1 равным нулю: φ₁=0. Тогда на основании второго закона Кирхгофа можно записать

Отсюда

Составление баланса мощностей

Мощность источника ЭДС положительна при совпадающих направлениях ЭДС и тока в ветви и отрицательна при противоположном направлении ЭДС и тока в ветви. Направление тока через источник ЭДС E₆ соответствуют направлению ЭДС этого элемента, а направление тока через источник ЭДС E₈ не соответствуют направлению своего ЭДС (рис.2). Значит, источник E₆ отдаёт мощность в цепь (т.е. его мощность положительна), а источник E₈ поглощает мощность из цепи (мощность источника ЭДС E₈ отрицательна).

Мощность источника тока определяется произведением тока и напряжения на его зажимах. Она положительна при противоположных направлениях напряжения на зажимах источника тока и тока источника. Направления напряжений на зажимах источников тока J₀₂ и J₀₈ противоположны соответствующим направлениям токов, поэтому их мощности положительны.

Составим уравнения баланса мощностей.

Мощность источников энергии равна:

Мощность потребителей энергии равна:

Так как мощность источников равна мощности тепловых потерь, то значения рассчитанных токов верны.

Определение тока в резисторе R₁ методом эквивалентного генератора

Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи.

Разделим электрическую цепь на две части: эквивалентный генератор и потребитель (рис. 3):

Рис. 3 Эквивалентная схема замещения

На схеме (рис. 3) искомый ток I₁ определим по закону Ома для замкнутой цепи:

,

где Е_э – ЭДС эквивалентного генератора. Её величину определяют как напряжения на зажимах генератора в режиме холостого хода (Е_э=U_хх);

R_э – внутреннее сопротивление эквивалентного генератора. его величина определяется как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов.

Для определения на зажимах генератора в режиме холостого хода исключим из рассматриваемой цепи (рис. 2) ветвь, содержащую сопротивление R₁, и представим остальную часть цепи (режим холостого хода):

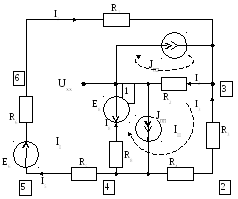
Рис. 4 К расчёту Е_э

Методом контурных токов определим токи в ветвях схемы. Составим уравнения по второму закону Кирхгофа относительно контурных токов:

или

В этих уравнениях контурные токи J₀₂ и J₀₈ равны токам источников тока. После подстановки численных значений получается система уравнений

Отсюда

I_I=0.791 (A), I_II=-0.949 (A).

тогда токи в ветвях схемы равны

I₇ = I_I =0.791 (А),

I₂ = I₁+ J₀₂ - I_II =2.740 (А).

Знание токов I₂ и I₇ позволяет определить напряжение холостого хода

Для расчёта внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник (рис. 4) в пассивный, при этом источники ЭДС закорачиваются а источники тока размыкаются:

Рис. 5 К расчёту R_э

Необходимо найти сопротивление между точками 6 и 1.

Заменим треугольник резисторов R₂ R₃, R₄ и R₈ звездой. Схема замещения представлена на рисунке 6.

Рис. 6. Схема замещения треугольника звездой

Найдём сопротивления R₂₈, R₃₄₈, R₂₃₄:

Тогда

Зная Е_э=U_xx и R_э, найдём ток в исследуемой ветви

7