
Инструкционная карта № 13 Проценты. Решение задач на проценты. 7 класс.
1. Процент – это сотая часть числа.
2. Чтобы перевести процент в десятичную дробь, нужно этот процент разделить на 100. Например: 15% = 0,15; 3% = 0,03; 135% = 1,35; 0,2% = 0,002.
Чтобы перевести десятичную дробь в процент, нужно эту дробь умножить на 100. Например: 0,42 = 42%; 0,5 = 50%; 1,23 = 123%; 0,0067 = 0,67%.
3. Чтобы найти процент от числа, нужно: 1) записать процент в виде десятичной дроби; 2) умножить данное число на эту дробь.
Например: найти 21% от 60. Решение: 1) 21% = 0, 21; 2) 60∙0,21 = 12,6.
4. Чтобы найти число по проценту, нужно: 1) записать процент в виде десятичной дроби; 2) разделить данное число на эту дробь.
Например: найти число, если 15% этого числа равны 12.
Решение: 1) 15% = 0,15; 2) 12 : 0,15 = 1200 : 15 = 80.
5. Выражение отношения в процентах. Нужно: 1) Разделить одно число на другое; 2)Умножить результат на 100.
Например: Из 150 писавших контрольную работу семиклассников 18 человек получили «5». Выразите в процентах, сколько учащихся выполнили работу на «5».
Решение:
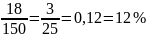 .
.
6. Решение задач на проценты.
Очень часто удобно решать задачи на проценты, используя пропорцию. Рассмотрим несколько примеров.
Задача 1. Цех по производству стульев перевыполнил свой месячный план на 7%, что составило 84 стула. Определите план выпуска стульев.
Решение. Пусть цех должен был сделать х стульев.
84 стула – 7%
Х стульев – 100%.
План
и количество выпущенных стульев
пропорциональны.
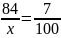 ;
х =
;
х =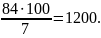
Итак, цех должен был выпустить 1200 стульев. Ответ: 1200 стульев.
Задача 2. Сколько процентов составляла праздничная скидка в магазине, если Маша приобрела товар стоимостью 125 рублей за 100 рублей?
Решение. Пусть скидка составила х процентов.
125 рублей – 100%
100 рублей – х %.
Зависимость
пропорциональная.
 ;
х =
;
х =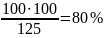 ;
Найдем скидку: 100% - 80% = 20%. Итак, скидка
в магазине 20%. Ответ:
20%.
;
Найдем скидку: 100% - 80% = 20%. Итак, скидка
в магазине 20%. Ответ:
20%.
7. Тренировочные задачи.
1. Оля взяла 800 г картофеля. После того как она почистила картофель, 15% ушло в отходы. Сколько граммов картофеля осталось?
2. Банковская ставка по вкладу составляет 8% годовых. Какой станет сумма вклада в 50 000 рублей через 3 года?
3. По итогам всероссийской переписи населения 2002 года численность мужского населения составляет 46% общей численности населения. Определите, сколько мужчин проживает на территории РФ, если численность постоянного населения составляет 145,2 млн. человек.
4. Сколько процентов
составляет
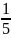 часть этого числа?
часть этого числа?
5. Килограмм картофеля в начале осени стоил 25 рублей. К середине осени цена на картофель понизилась на 20%, а к концу осени понизилась еще на 25%. Сколько рублей стоил килограмм картофеля в конце осени?
6. В двух сосудах различной формы находится одинаковое количество воды. Через некоторое время в первом сосуде испарилось 40% воды, а во втором сосуде количество воды уменьшилось в полтора раза. В каком сосуде осталось больше воды?
7. Суточная норма потребления белков в среднем составляет 70 г. В 100 г отварного мяса содержится 20% белков. Кусок мяса какого веса содержит суточную норму белков?
8. В одном школьном классе находится 24 компьютера, а в другом компьютерном классе их на 25% больше. Сколько компьютеров находится во втором классе?
9. Турист шел по ровной местности со скоростью 8 км/ч, а затем по холмистой – со скоростью 2 км/ч. На сколько процентов снизилась скорость туриста?
10. Повышение цены
товара на 5% можно записать различными
способами. В какой из четырех записей
содержится ошибка? (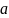 - первоначальная цена товара).
- первоначальная цена товара).
А. 𝑎
+ 5 Б.
𝑎
+
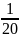 𝑎
В.
𝑎
+ 0,05𝑎
Г. 1,05𝑎
𝑎
В.
𝑎
+ 0,05𝑎
Г. 1,05𝑎
11. Скорость набора текста на клавиатуре компьютера у Димы на 60% больше, чем у Толи. Во сколько раз скорость набора Димы больше скорости набора Толи?
12. Сколько граммов спирта надо добавить к 600 граммам 16%-ного раствора йода в спирте, чтобы получить 10%-ный раствор йода?
13. На один вид товаров в магазине предоставлялась скидка 15%, а на другой – 20%. До того как в магазине начали действовать скидки, цена изделия первого вида составляла 300 рублей, а цена изделия второго вида – 320 рублей. Выясните, цена изделия какого вида будет меньшей после начала действия скидок.
14. Туристы за первый день похода прошли 30 км, за второй день – 36 км, за третий день – 43,2 км. На сколько процентов ежедневно увеличивалась протяженность маршрута туристов?
15. Количество осадков в 3 раза превысило среднее количество осадков за данный период. На сколько процентов было превышено количество осадков?
16. Из 59 девятиклассников школы 22 человека приняли участие в городских спортивных соревнованиях. Сколько примерно процентов девятиклассников приняли участие в соревнованиях?
17. В 9-х классах школы 92 учащихся. В районных соревнованиях по спортивному ориентированию участвовали 15 девятиклассников. Сколько примерно процентов девятиклассников участвовали в соревнованиях?
18. Масса сплава, состоящего из олова и свинца, равна 600 г. В сплаве 68% олова. Найдите массу свинца.
19. Смешали 3 кг шоколадных конфет и 2 кг карамели. Сколько процентов составляет карамель от полученной смеси конфет?
20. Сталь содержит 6% примесей. Сколько тонн примесей в 20 т стали?
21. Цену на товар снизили сначала на 20%, а затем еще на 15%. После этого товар стал стоить 238 рублей. Какова была первоначальная цена товара?
! 22. Разность двух чисел составляет 80% уменьшаемого. На сколько процентов уменьшаемое больше вычитаемого? (80%)
23. Сколько процентов соли содержится в растворе, если в 200 г раствора содержится 150 г воды?
! 24. На сколько процентов увеличится дробь, если ее числитель увеличить на 60%, а знаменатель уменьшить на 20%?
25. Яблоки при сушке теряют 84% своей массы. Сколько надо взять свежих яблок, чтобы получить 20 кг сушеных?
26. Цену на костюм снизили на 15%, в результате чего он стоит теперь 1700 рублей. Сколько стоил костюм до снижения цены?
27. Цену на книгу снизили на 10%, в результате чего она стоит теперь 45,9 рублей. Сколько стоила книга до снижения цены?
28. При помоле пшеницы получается 80% муки. Сколько пшеницы нужно смолоть, чтобы получить 220 кг пшеничной муки?
29. Из 2000 зерен пшеницы взошло 1800. Определите процент всхожести семян.
30. Найдите 60% от
числа 1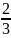 .
.
31. Цех по производству стульев перевыполнил свой месячный план на 7%, что составило 84 стула. Определите план выпуска стульев.
32. Кондитерская фабрика перевыполнила свой годовой план на 207 тонн конфет, что составило 9% от годового плана. Определите годовой план выпуска конфет (в тоннах). 33. Цех должен изготовить 690 деталей за неделю. Известно, что за два дня цех успел изготовить 40% недельного плана. Определите, сколько деталей изготовил цех за два дня?
34. Магазин закупает товар по 800 рублей. И повышает цену на 176 рублей. На сколько процентов магазин поднимает цену товара?
35. За полгода бригада успела провести 1 079 м газового трубопровода, что составляет 65% от годового плана. Определите годовой план бригады.
36. Магазин во время распродажи делает скидку на товар в размере 350 рублей. На сколько процентов магазин снизил цену товара, если до распродажи его цена составляла 4375 рублей?
37. В таблице представлено распределение числа мальчиков и девочек, обучающихся в 9 «А» и 9«Б» классах некоторой школы. Сколько процентов составляет общее количество девочек от общего числа всех девятиклассников?
|
9«А» |
9«Б» |
Мальчиков |
15 |
15 |
Девочек |
9 |
11 |
38. Цена установки окна в квартире составляет 12% от его стоимости. Определите стоимость окна, если известно, что его установка стоит 498 рублей.
39. Магазин, во время распродажи, делает скидку на товар в размере 182 рублей. На сколько процентов магазин снизил цену товара, если до распродажи его цена составляла 3640 рублей?
40. Стоимость установки входной двери в квартире составляет 5% от ее цены. Определите цену двери, если известно, что ее установка стоит 342 рубля.
41. Цех по производству колбасных изделий за полмесяца выработал 56% месячной нормы, что составило 2520 кг. Определите месячный план этого цеха.
42. В таблице представлено распределение оценок за контрольную работу по математике в 6 классе. Сколько процентов учащихся получили оценку «3»?
Оценка |
«2» |
«3» |
«4» |
«5» |
число учащихся |
3 |
6 |
12 |
3 |
