
Опорный конспект лекций / Опорный конспект к лекции №6
.docxОПОРНЫЙ КОНСПЕКТ
по теме «Монотонные последовательности. Критерий сходимости. Число e»
|
Монотонные последовательности |
Характеристическое
свойство
|
Обозначение |
|
Возрастающая (неубывающая) |
|
|
|
Строго возрастающая |
|
|
|
Убывающая (невозрастающая) |
|
|
|
Строго убывающая |
|
|
Теорема о существовании предела монотонной последовательности |
|
|
Критерий сходимости монотонной последовательности |
|
Монотонная последовательность ограничена тогда и только тогда, когда она сходится |
Подпоследовательностью
последовательности
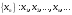 называется
последовательность, составленная из
подмножества членов данной последовательности
в порядке возрастания их номеров
называется
последовательность, составленная из
подмножества членов данной последовательности
в порядке возрастания их номеров
|
Т |
Если
последовательность
|
|
С |
Если
две подпоследовательности одной и
той же последовательности
|
|
Лемма Больцано – Вейерштрасса |
|
|
Признак сходимости Больцано – Коши |
|
Для
того чтобы у последовательности
|
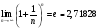








 монотонно
возрастает (убывает) и ограничена
сверху (снизу), то у нее существует
конечный предел, равный
монотонно
возрастает (убывает) и ограничена
сверху (снизу), то у нее существует
конечный предел, равный
 (
( )
) монотонно
возрастает (убывает), но сверху (снизу)
не ограничена, то
монотонно
возрастает (убывает), но сверху (снизу)
не ограничена, то
 (
( )
) сходится
и ее предел равен
сходится
и ее предел равен
 ,
то любая ее подпоследовательность
также сходится и имеет тот же самый
предел
,
то любая ее подпоследовательность
также сходится и имеет тот же самый
предел сходятся
к различным пределам, то
сходятся
к различным пределам, то
 не
существует
не
существует существовал
конечный предел, необходимо и достаточно,
чтобы
существовал
конечный предел, необходимо и достаточно,
чтобы
