
Опорный конспект лекций / Опорный конспект к лекции №7
.docxОПОРНЫЙ КОНСПЕКТ
по теме «Предел функции в точке и на бесконечности»
Определение предела функции
|
Название
предела функции
|
Определение |
Обозначение |
|
|
в точке x0 |
по Коши |
|
|
|
по Гейне |
|
||
|
на беско- нечности |
|
|
|
Свойства предела функции в точке
|
№ |
Свойство |
|
|
Если
функция
|
|
|
Если функция f(x) имеет предел в точке х0, то существует окрестность этой точки (за исключением, быть может, самой точки х0), на которой функция ограничена |
|
|
Если
существует предел функции f(x)
в точке х0,
равный числу
|
|
|
Если
функции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
всех элементарных функций в любой
точке их области определения имеет
место равенство
|
|
Критерий Коши существования предела функции в точке |
|
|
Т-13 |
Для
того чтобы функция
|













 в точке
в точке
 имеет предел, то он единственный
имеет предел, то он единственный то существует такая окрестность точки
х0,
на которой функция имеет тот же знак,
что и число А
то существует такая окрестность точки
х0,
на которой функция имеет тот же знак,
что и число А и
и
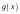 имеют пределы в точке
имеют пределы в точке
 то справедливы формулы:
то справедливы формулы: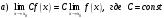




 имела предел при
имела предел при
 ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
