
Опорный конспект лекций / Опорный конспект к лекции №3
.docОПОРНЫЙ КОНСПЕКТ
по теме «Комплексные числа и действия над ними»
Понятие комплексного числа (к.ч.)
|
Название |
Определение |
Обозначение |
|
Комплексное
число
|
упорядоченная
пара действительных чисел
|
|
|
Мнимая единица |
комплексное
число
|
|
|
Действительная
часть к.ч. |
число
|
|
|
Мнимая
часть к.ч. |
число
|
|
|
Равные комплексные числа
|
действительные и мнимые части чисел соответственно равны
|
|
|
Комплексно сопряженное число к
числу
|
число, у которого действительная часть остается без изменения, а мнимая часть меняется на противоположную |
|
|
Комплексная плоскость |
прямоугольная
декартова система координат, где
комплексное число
|
|
|
Алгебраическая форма записи к.ч. |
сумма действительной и мнимой части, умноженной на мнимую единицу |
|
|
Модуль к.ч. |
длина
радиус-вектора точки |
|
|
Аргумент к.ч. |
угол
между радиус-вектором точки
|
|
|
Главное значение аргумента к.ч. |
угол
|
|
|
Тригонометрическая форма записи к.ч. |
|
|
|
Формула Эйлера |
|
|
|
Показательная форма записи к.ч. |
|
|
Свойства комплексно сопряженных чисел
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
|
5) |
|
|
6) |
|
Действия над комплексными числами в алгебраической форме
Пусть



|
Действие |
Формула |
|
Сложение |
|
|
Вычитание |
|
|
Умножение |
|
|
Деление |
|
Действия над комплексными числами
в тригонометрической и показательной формах
Пусть
 ,
,
 ,
,

|
Действие |
Формула |
|
Умножение |
|
|
Деление |
|
|
Возведение в степень (формула Муавра) |
|
|
Извлечение корня
|
|


 и
и

 или
или

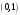
 ,
причем
,
причем







 и
и

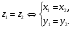


 изображается точкой
изображается точкой
 с
абсциссой
с
абсциссой
 и ординатой
и ординатой







 и положительным направлением оси
и положительным направлением оси



 между радиус-вектором точки
между радиус-вектором точки
 и положительным направлением оси
и положительным направлением оси
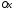 в границах
в границах

 причем
причем








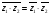

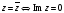



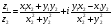



 -й
степени из к.ч.
-й
степени из к.ч.
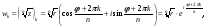
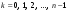 ,
причем все
значения корня
,
причем все
значения корня
 ,
,
 расположены на окружности с центром
в начале системы координат и радиусом
расположены на окружности с центром
в начале системы координат и радиусом
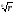 в вершинах правильного вписанного в
окружность n-угольника
в вершинах правильного вписанного в
окружность n-угольника