
Опорный конспект лекций / Опорный конспект к лекции №5
.docxОПОРНЫЙ КОНСПЕКТ
по теме «Бесконечно большие и бесконечно малые последовательности.
Свойства сходящихся последовательностей. Виды неопределенностей»
Бесконечно большие и бесконечно малые последовательности
|
Название |
Определение |
|
Бесконечно
малая
последовательность
|
|
|
Бесконечно
большая
последовательность
|
|
Свойства бесконечно малых и бесконечно больших последовательностей
|
№ |
Свойство |
Обозначение |
|
|
Сумма, разность и произведение конечного числа бесконечно малых последовательностей есть также бесконечно малая последовательность |
|
|
|
Бесконечно малая последовательность ограничена |
|
|
|
Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность |
|
|
|
Если
|
|
|
|
Если
|
|
|
|
Если
|
|
|
|
Если
|
|
|
|
Если
|
|
|
|
Если
|
|
Свойства сходящихся последовательностей
|
№ |
Свойство |
|
|
Если последовательность имеет предел, то он всегда определен единственным образом |
|
|
Если все элементы числовой последовательности принимают одно и то же постоянное значение, то предел этой последовательности будет равен самой постоянной |
|
|
Для
того чтобы последовательность
|
|
|
Сходящаяся последовательность ограничена |
|
|
Если
|
|
|
(Предельный
переход в неравенстве)
Если
|
|
|
(Лемма
о сжатой переменной)
Если
|
|
|
Если
|
|
|
Если
|
Виды неопределенностей
Чтобы
вычислить предел в случае неопределенности
вида
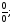





 ,
необходимо тождественно преобразовать
выражение, стоящее под знаком предела
,
необходимо тождественно преобразовать
выражение, стоящее под знаком предела




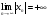
 –
бесконечно большая последовательность,
то, начиная с некоторого номера
–
бесконечно большая последовательность,
то, начиная с некоторого номера
 ,
определена последовательность
,
определена последовательность
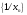 ,
и она есть бесконечно малая
последовательность. Наоборот, если
,
и она есть бесконечно малая
последовательность. Наоборот, если
 –
бесконечно малая последовательность
и все
–
бесконечно малая последовательность
и все
 ,
то
,
то
 есть
бесконечно большая последовательность
есть
бесконечно большая последовательность и
и
 –
бесконечно большие последовательности,
причем
–
бесконечно большие последовательности,
причем

 ,
то
,
то


 и
и
 –
бесконечно большие последовательности,
причем
–
бесконечно большие последовательности,
причем
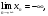
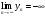 ,
то
,
то


 –
бесконечно большая последовательность,
причем
–
бесконечно большая последовательность,
причем
 а
а
 –
сходящаяся последовательность, причем
–
сходящаяся последовательность, причем
 ,
то
,
то


 и
и
 –
бесконечно большие последовательности,
то
–
бесконечно большие последовательности,
то


 –
бесконечно большая последовательность,
а
–
бесконечно большая последовательность,
а
 –
сходящаяся последовательность, причем
–
сходящаяся последовательность, причем
 ,
то
,
то
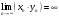

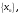 была
сходящейся и
была
сходящейся и
 необходимо
и достаточно, чтобы выполнялось
равенство
необходимо
и достаточно, чтобы выполнялось
равенство
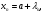 где
где
 – бесконечно малая последовательность
– бесконечно малая последовательность
 ,
причем
,
причем
 ,
то, начиная с некоторого номера
,
то, начиная с некоторого номера
 ,
,


 и, начиная с некоторого номера
и, начиная с некоторого номера
 ,
,
 ,
то
,
то

 и, начиная с некоторого номера
и, начиная с некоторого номера
 ,
,
 ,
то
,
то


 ,
то
,
то
 , то
, то
 ,
, ,
,