
- •Опорный конспект
- •Формула бинома Ньютона
- •Треугольник Паскаля
- •Метод математической индукции
- •Основные понятия математической логики
- •Логические операции над высказываниями
- •Типы теорем
- •Основные понятия теории множеств
- •Операции над множествами
- •Сравнение свойств операций над высказываниями и множествами
- •Ограниченные и неограниченные множества. Грани числовых множеств
- •Функции действительной переменной
Ограниченные и неограниченные множества. Грани числовых множеств
|
Название |
Определение |
|
Множество
М – верхняя грань множества Х |
|
|
Множество
т – нижняя грань множества Х |
|
|
Множество
|
|
|
Множество
|
|
|
Супремум
|
Наименьшая
из верхних граней множества
Х, т.е.
//////////////////////
|
|
Инфимум
|
Наибольшая из нижних граней множества Х, т.е.
//////////////////////////
|
|
Теорема о существовании супремума и инфимума числового множества |
|
|
Т-1 |
Если
числовое множество
|
Функции действительной переменной
|
Название |
Определение |
Обозначение |
|
Функция
(отображение)
из
|
Правило,
по которому каждому элементу множества
|
|
|
Обратная функция |
Правило,
по которому каждому элементу множества
|
или
|
|
Взаимно обратные функции |
Функции
|
|
|
Сложная функция |
Функция
|
|
|
Основные способы задания функции |
||
|
Название |
Сущность способа |
Пример |
|
Табличный |
Приводится таблица, указывающая значения функции для значений аргумента |
таблицы значений тригонометрических функций |
|
Графический |
Изображается
график функции (График
функции
|
|
|
Явный аналитический |
Приводится формула, связывающая значения аргумента со значениями функции |
|
|
Неявный аналитический |
Говорят,
что функция
|
|
|
Параметрическими уравнениями |
Зависимость
значений функции от аргумента выражена
опосредованно через некоторый параметр
(Параметрическими
уравнениями
линии называют уравнения вида
|
|

 ограниченное
сверху;
ограниченное
сверху;

 ограниченное
снизу;
ограниченное
снизу;
 ограниченное
ограниченное
 неограниченное
неограниченное
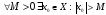
 ,
или
точная верхняя грань множества
Х
,
или
точная верхняя грань множества
Х

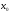






 ,
или
точная нижняя грань множества
Х
,
или
точная нижняя грань множества
Х








 не является пустым и ограничено сверху,
то у него существует
не является пустым и ограничено сверху,
то у него существует
 .
Если числовое множество
.
Если числовое множество
 не является пустым и ограничено снизу,
то у него существует
не является пустым и ограничено снизу,
то у него существует

 в
в
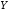
 ставится
в соответствие единственный элемент
ставится
в соответствие единственный элемент

 или
или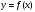
 – аргумент
функции
– аргумент
функции –
значение
функции
–
значение
функции –
область
определения
–
область
определения –
множество
значений
–
множество
значений –
образ
элемента
–
образ
элемента

 –
прообраз
элемента
–
прообраз
элемента

 ставится
в соответствие единственный элемент
ставится
в соответствие единственный элемент



 и
и
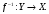 Их графики симметричны относительно
прямой
Их графики симметричны относительно
прямой


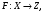 если
даны две функции
если
даны две функции
 и
и

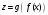
 – это множество пар вида
– это множество пар вида
 ,
изображаемых точками на плоскости)
,
изображаемых точками на плоскости)


 задана
неявно
уравнением
задана
неявно
уравнением
 где
F
– выражение от переменных x,
y
при условии
где
F
– выражение от переменных x,
y
при условии




 где
где
 – параметр, а
– параметр, а
 и
и
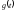 – функции параметра
– функции параметра
 )
)
