
- •Опорный конспект
- •Формула бинома Ньютона
- •Треугольник Паскаля
- •Метод математической индукции
- •Основные понятия математической логики
- •Логические операции над высказываниями
- •Типы теорем
- •Основные понятия теории множеств
- •Операции над множествами
- •Сравнение свойств операций над высказываниями и множествами
- •Ограниченные и неограниченные множества. Грани числовых множеств
- •Функции действительной переменной
Опорный конспект
по теме «Бином Ньютона. Метод математической индукции.
Элементы математической логики и теории множеств. Грани числовых множеств»
Формула бинома Ньютона

где
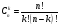 – биномиальные
коэффициенты
– биномиальные
коэффициенты
Свойства формулы бинома Ньютона:
-
в разложении двучлена
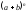 по формуле
Ньютона содержится
по формуле
Ньютона содержится
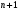 член;
член; -
в разложении
 показатель степени
показатель степени
 убывает от
убывает от
 до
до
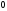 ,
а показатель степени
,
а показатель степени
 возрастает от
возрастает от
 до
до
 ;
; -
сумма показателей степеней
 и
и
 в каждом члене равна
в каждом члене равна
 ;
; -
биномиальные коэффициенты членов, равноудаленных от концов разложения, равны между собой.
Треугольник Паскаля
Числа
в строке с определенным номером
 ,
,
 ,
являются последовательными коэффициентами
в формуле для данного
,
являются последовательными коэффициентами
в формуле для данного
 .
.
Показатель степени

Метод математической индукции
Доказательство
истинности утверждения
 при всех значениях натуральной переменной
при всех значениях натуральной переменной
 методом
математической индукции:
методом
математической индукции:
-
непосредственной проверкой убедиться в истинности
 ;
; -
допустить, что
 истинно
для любого
истинно
для любого
 ;
; -
доказать, что
 истинно
для всех
истинно
для всех
 ,
,
 .
.
Основные понятия математической логики
|
Понятие |
Определение |
|
Высказывание |
повествовательное предложение, относительно которого имеет смысл говорить, что его содержание истинно (1) или ложно (0) в данных условиях места и времени |
|
Элементарное высказывание |
высказывание, представляющее собой одно утверждение, нерасчленимое на более простые высказывания без потери его смысловой нагрузки |
|
Составное высказывание |
высказывание, которое можно расчленить на элементарные высказывания |
|
Предикат |
неопределенное
высказывание, т.е. предложение
|
|
Тавтология |
составное высказывание, истинное при любых предположениях о входящих в него элементарных высказываниях |
Логические операции над высказываниями
|
Название |
Определение |
Обозначение |
Чтение |
|
Отрицание |
логическая
операция, которая утверждает, что
высказывание
|
|
не
|
|
Двойное отрицание |
утверждение
о том, что высказывание
|
|
не
|
|
Импликация |
высказывание,
которое считается ложным, если
|
|
из
|
|
Эквиваленция |
высказывание
« |
|
|
|
Конъюнкция (логическое и, логическое умножение) |
одновременное
выполнение двух свойств
|
|
|
|
Дизъюнкция (логическое или, логическое сложение) |
высказывание,
когда либо имеет место
|
|
|
Таблица истинности алгебраических операций над высказываниями
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |

 ,
которое при каждом конкретном
,
которое при каждом конкретном
 превращается
в некоторое высказывание
превращается
в некоторое высказывание не выполняется
не выполняется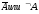

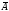 не выполняется
не выполняется

 истинно, а
истинно, а
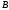 –
ложно, и истинным во всех остальных
случаях
–
ложно, и истинным во всех остальных
случаях
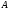 следует
следует
 тогда и только тогда, когда
тогда и только тогда, когда
 »
»
 равносильно
равносильно

 и
и

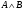 или
или
 &
&

 и
и

 (но не
(но не
 ),
либо имеет место
),
либо имеет место
 (но не
(но не
 ),
либо имеют место
),
либо имеют место
 и
и
 одновременно
одновременно
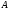 или
или








