
Опорный конспект лекций / Опорный конспект к лекции №9
.docxОПОРНЫЙ КОНСПЕКТ
по теме «Гиперболические функции и их пределы. Сравнение функций.
Эквивалентные функции и их применение»
Гиперболические функции и их графики
|
Название |
Определение |
Графики |
|
Гиперболический синус |
|
|
|
Гиперболический косинус |
|
|
|
Гиперболический тангенс |
|
|
|
Гиперболический котангенс |
|
|
Свойства
гиперболического синуса


Свойства
гиперболического косинуса


Свойства
гиперболического тангенса


Свойства
гиперболического котангенса


Основные тождества
|
№ |
Название |
Формула |
|
|
|
Основное тождество |
|
|
|
|
Четность, нечетность |
|
|
|
|
|||
|
|
Формулы сложения |
|
|
|
|
|
||
|
|
Формулы двойного угла |
|
|
|
|
|||
|
|
|
||
|
|
|||
|
|
Формулы суммы |
|
|
|
|
|
||
|
|
|||
|
|
Формулы понижения степени |
|
|
Пределы гиперболических функций



Сравнение бесконечно малых функций
Пусть
 ,
,
 – бесконечно малые функции при
– бесконечно малые функции при
 ,
причем
,
причем
 – конечная или бесконечная точка, в
которой функции могут быть не определены.
– конечная или бесконечная точка, в
которой функции могут быть не определены.
|
№
|
Название |
Обозначение (при
|
Признак |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом введенных определений можно заметить, что:
-
 – бесконечно
малая функция при
– бесконечно
малая функция при
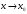 тогда и только тогда, когда
тогда и только тогда, когда
 ;
; -
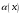 – ограниченная
функция при
– ограниченная
функция при
 тогда и только тогда, когда
тогда и только тогда, когда
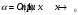 .
.
Для определения порядка k одной бесконечно малой функции относительно другой можно рекомендовать такой порядок действий:
-
написать под знаком предела отношение
 и упростить его;
и упростить его; -
предположить возможное значение
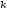 ,
при котором будет существовать конечный
предел, не равный нулю;
,
при котором будет существовать конечный
предел, не равный нулю; -
проверить предположение, вычислив предел.
Сравнение бесконечно больших функций
|
№ п/п |
Название |
Обозначение (при
|
Признак |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Свойства эквивалентных функций
-
Предел отношения бесконечно малых функций при
 равен пределу отношения эквивалентных
им бесконечно малых функций при
равен пределу отношения эквивалентных
им бесконечно малых функций при
 .
. -
Предел отношения бесконечно больших функций при
 равен пределу отношения эквивалентных
им бесконечно больших функций при
равен пределу отношения эквивалентных
им бесконечно больших функций при
 .
. -
Две бесконечно малые при
 функции
функции
 и
и
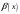 эквивалентны тогда и только тогда,
когда их разность является бесконечно
малой функцией более высокого порядка,
чем каждая из этих функций, т.е.
эквивалентны тогда и только тогда,
когда их разность является бесконечно
малой функцией более высокого порядка,
чем каждая из этих функций, т.е.
 и
и
 при
при
 .
. -
Сумма конечного числа бесконечно малых функций эквивалентна тому слагаемому, которое имеет самый низкий порядок.
-
(О замене переменных) Если
 и
и
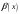 – бесконечно малые функции при
– бесконечно малые функции при
 ,
а в некоторой проколотой окрестности
точки
,
а в некоторой проколотой окрестности
точки
 функция
функция
 отлична от нуля и при
отлична от нуля и при
 стремится к
стремится к
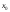 ,
то сложные функции
,
то сложные функции
 и
и
 эквивалентны при
эквивалентны при

Нахождение пределов
Асимптотическую эквивалентность удобно применять при вычислении пределов отношений или произведений. Тогда каждый член отношения или произведения можно заменить эквивалентной ему функцией, отчего искомый предел не изменится. При вычислении предела показательно-степенной функции часто возникает необходимость применить формулу
 .
.




















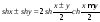






 )
) и
и
 – бесконечно
малые одинакового порядка малости
– бесконечно
малые одинакового порядка малости



 – бесконечно
малая более высокого порядка малости,
чем
– бесконечно
малая более высокого порядка малости,
чем
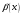


 – бесконечно
малая более низкого порядка малости,
чем
– бесконечно
малая более низкого порядка малости,
чем


 и
и
 – эквивалентные
бесконечно малые
– эквивалентные
бесконечно малые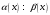

 – бесконечно
малая
– бесконечно
малая
 -го
порядка малости относительно бесконечно
малой
-го
порядка малости относительно бесконечно
малой




 и
и
 –
несравнимые бесконечно малые функции
–
несравнимые бесконечно малые функции
 )
)
 и
и
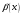 – бесконечно
большие одинакового порядка роста
– бесконечно
большие одинакового порядка роста


 – бесконечно
большая более высокого порядка роста,
чем
– бесконечно
большая более высокого порядка роста,
чем



 – бесконечно
большая более низкого порядка роста,
чем
– бесконечно
большая более низкого порядка роста,
чем


 и
и
 – эквивалентные
бесконечно большие
– эквивалентные
бесконечно большие

 – бесконечно
большая
– бесконечно
большая
 -го
порядка роста относительно бесконечно
большой
-го
порядка роста относительно бесконечно
большой



 и
и
 –
несравнимые бесконечно большие функции
–
несравнимые бесконечно большие функции