
Опорный конспект лекций / Опорный конспект к лекции №4
.docОПОРНЫЙ КОНСПЕКТ
по теме «Основная теорема алгебры.
Разложение многочлена на множители.
Предел числовой последовательности»
Многочлены
|
Название |
Определение |
|
Многочлен (полином)
|
выражение
вида
|
|
Коэффициенты многочлена |
числа
|
|
Старший коэффициент |
число
|
|
Свободный член многочлена |
число
|
|
Одночлен |
слагаемое
вида
|
|
Приведенный многочлен |
многочлен,
у которого
|
|
Многочлен нулевой степени |
многочлен
вида
|
|
Равные многочлены |
многочлены, у которых равны все их коэффициенты при соответствующих степенях переменной х |
|
Корень
многочлена
|
число
|
|
Корень
кратности
|
число
|
Операции над многочленами
Пусть
 ,
,

|
Операция |
Суть операции |
|
Умножение многочлена на
число
|
|
|
Сложение многочленов |
|
|
Умножение многочленов |
каждый член одного многочлена умножают на каждый член второго многочлена, полученные результаты складывают и приводят подобные |
|
Деление многочленов |
если
степень делителя
|
Многочлен
 делится нацело на
делится нацело на
 если остаток
если остаток
 равен нулю, т.е.
равен нулю, т.е.

|
Теорема Безу |
|
|
Т-2 |
Остаток
от деления многочлена
|
|
Следствие из теоремы Безу |
|
|
С-1 |
Число
х0
является корнем многочлена
|
|
Основная теорема алгебры |
|
|
Т-3 |
Всякий отличный от константы многочлен с комплексными коэффициентами имеет комплексный корень |
|
Следствие из основной теоремы алгебры |
|
|
С-2 |
Любой
многочлен
|
Разложение многочлена на множители
Разложение
на множители многочлена
 с действительными коэффициентами имеет
вид:
с действительными коэффициентами имеет
вид:
 где
где
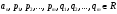 ;
;
 –
корни многочлена
–
корни многочлена
 кратности
кратности
 соответственно;
соответственно;
 ,
причем
,
причем

Квадратные
трехчлены
 не имеют действительных корней и
соответствуют паре комплексно сопряженных
корней некоторой кратности.
не имеют действительных корней и
соответствуют паре комплексно сопряженных
корней некоторой кратности.
|
Т-4 |
Если
|
|
Т-5 |
Пусть
|
Понятие числовой последовательности
Числовой
последовательностью
называется
функция натурального аргумента
 которая каждому натуральному числу
которая каждому натуральному числу
 ставит в соответствие число
ставит в соответствие число
 ,
причем
,
причем
 называют
называют
 -м
членом (общим членом) последовательности,
а формулу
-м
членом (общим членом) последовательности,
а формулу
 –формулой
общего члена последовательности
–формулой
общего члена последовательности
Виды числовых последовательностей
|
Название
последовательности
|
Определение |
|
Ограниченная сверху последовательность |
|
|
Ограниченная снизу последовательность |
|
|
Ограниченная последовательность |
последовательность, одновременно ограниченная и снизу, и сверху, т.е.
|
Действия над числовыми последовательностями
-
Умножение последовательности на число:
 .
.
-
Сложение и вычитание последовательностей:
 .
.
-
Умножение последовательностей:
 .
.
-
Деление последовательностей:
 ,
,
 .
.
Предел числовой последовательности
|
Название |
Определение |
Обозначение |
|
Предел последовательности |
Число
|
или
|
|
Сходящаяся последовательность |
Последовательность
|
|
|
Расходящаяся последовательность |
Последовательность
|
|






 -й
степени
от переменной
-й
степени
от переменной








 ,
который представляет собой число
,
который представляет собой число
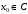 ,
для которого
,
для которого

 многочлена
многочлена

 ,
для которого
,
для которого
 и
и
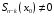



 меньше
или равна степени делимого
меньше
или равна степени делимого ,
деление выполняется по правилу «деления
углом»:
,
деление выполняется по правилу «деления
углом»:


 где
где
 – частное, представляющее собой
многочлен,
– частное, представляющее собой
многочлен,
 – остаток, причем степень остатка
меньше степени делителя
– остаток, причем степень остатка
меньше степени делителя на
на
 ,
где
,
где
 ,
равен значению многочлена в точке
,
равен значению многочлена в точке
 ,
т.е.
,
т.е.

 тогда и только тогда, когда
тогда и только тогда, когда
 делится нацело на
делится нацело на

 -й
степени
может
быть представлен в виде разложения
на множители:
-й
степени
может
быть представлен в виде разложения
на множители:
 ,
где
,
где
 ,
т.е. имеет
,
т.е. имеет
 корней
корней
 является корнем многочлена
является корнем многочлена
 -й
степени
с действительными коэффициентами, то
-й
степени
с действительными коэффициентами, то
 также является корнем этого многочлена
также является корнем этого многочлена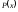 – приведенный многочлен с целыми
коэффициентами. Если он имеет целые
корни, то они содержатся среди целых
делителей свободного члена
– приведенный многочлен с целыми
коэффициентами. Если он имеет целые
корни, то они содержатся среди целых
делителей свободного члена



 называется пределом
последовательности
называется пределом
последовательности
 при
при
 ,
если
,
если



 называется
сходящейся,
если число
называется
сходящейся,
если число
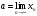 конечное
конечное называется
расходящейся,
если
называется
расходящейся,
если
 или предел не существует
или предел не существует

