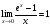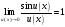Опорный конспект лекций / Опорный конспект к лекции №8
.docxОПОРНЫЙ КОНСПЕКТ
по теме «Бесконечно большие и бесконечно малые функции.
Замечательные пределы»
Бесконечно большие и бесконечно малые функции
|
Название |
Определение |
Обозначение |
|
Бесконечно
большая функция
при
|
|
|
|
Бесконечно
большая функция
при
|
|
|
|
Бесконечно малая функция
при
|
|
|
|
Бесконечно малая функция
при
|
|
|
Свойства бесконечно больших и бесконечно малых функций
|
№ |
Свойство |
|
|
Число
|
|
|
Если
|
|
|
Если
|
|
|
Сумма,
разность и произведение конечного
числа бесконечно малых (бесконечно
больших) функций при
|
|
|
Произведение
бесконечно малой функции при
|
|
|
Произведение бесконечно малой (бесконечно большой) функции на число есть бесконечно малая (бесконечно большая) функция |
|
|
Сумма бесконечно большой функции и ограниченной функции есть бесконечно большая функция
|
|
|
Частное
при делении постоянной
|
|
|
Частное
при делении постоянной
|
Замечательные пределы и их следствия
|
1. |
|
2. |
|
|
1.1 |
|
2.1. |
|
|
1.2 |
|
2.2. |
|
|
1.3 |
|
2.3. |
|
|
1.4 |
|
2.4. |
|
|
1.5 |
|
2.5. |
|
|
1.6 |
|
2.6. |
|
Обобщенная таблица замечательных пределов
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|






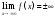








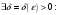
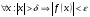

 является пределом функции
является пределом функции
 в точке
в точке
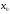 тогда и только тогда, когда существует
бесконечно малая функция
тогда и только тогда, когда существует
бесконечно малая функция
 при
при
 такая, что
такая, что

 –
бесконечно малая функция и выполняется
неравенство
–
бесконечно малая функция и выполняется
неравенство то
то
 – также бесконечно малая функция
– также бесконечно малая функция –
бесконечно большая функция и выполняется
неравенство
–
бесконечно большая функция и выполняется
неравенство ,
то
,
то
 –
также бесконечно большая функция
–
также бесконечно большая функция является бесконечно малой (бесконечно
большой функцией)
является бесконечно малой (бесконечно
большой функцией)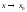 на ограниченную функцию является
бесконечно малой
на ограниченную функцию является
бесконечно малой на бесконечно малую функцию при
на бесконечно малую функцию при
 является
бесконечно большой при
является
бесконечно большой при

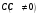 на бесконечно большую функцию при
на бесконечно большую функцию при
 является
бесконечно малой при
является
бесконечно малой при