КР 1, Вар 2

Контрольная работа № 1.

Основы векторной алгебры и аналитической геометрии

Задачи 1–10

Даны четыре вектора , , и , заданные в прямоугольной декартовой системе координат. Требуется: 1) вычислить скалярное произведение ; 2) вычислить векторное произведение ; 3) показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Задача  2: ; ; ; .

Решение:

1) Вычислим скалярное произведение

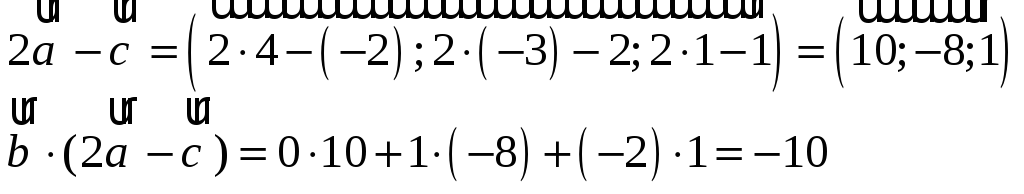
2) Вычислим векторное произведение

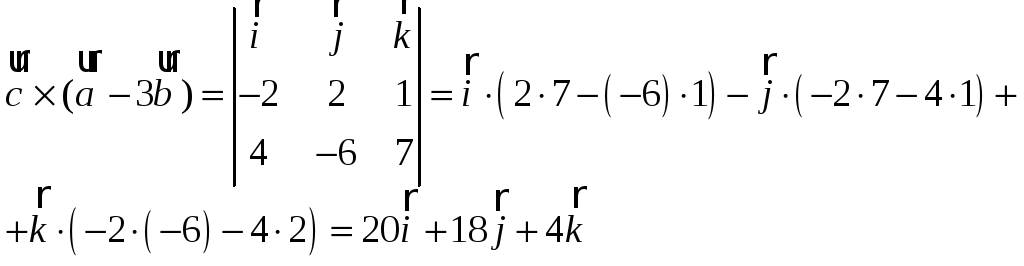
3) Покажем, что векторы образуют базис и найти координаты вектора в этом базисе.

Базис образуют линейно независимые векторы.

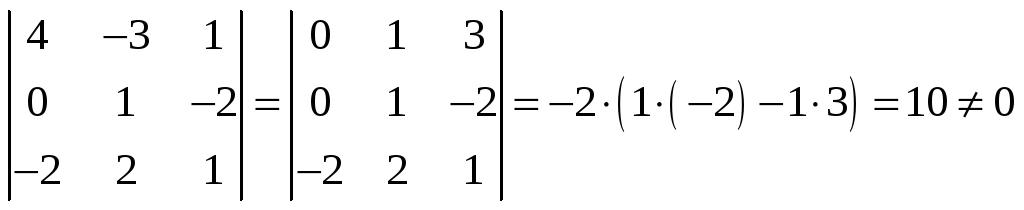
Таким образом, векторы линейно независимы и, соответственно, могут образовывать базис.

Найдем координаты вектора x в этом базисе.

Получим систему уравнений.

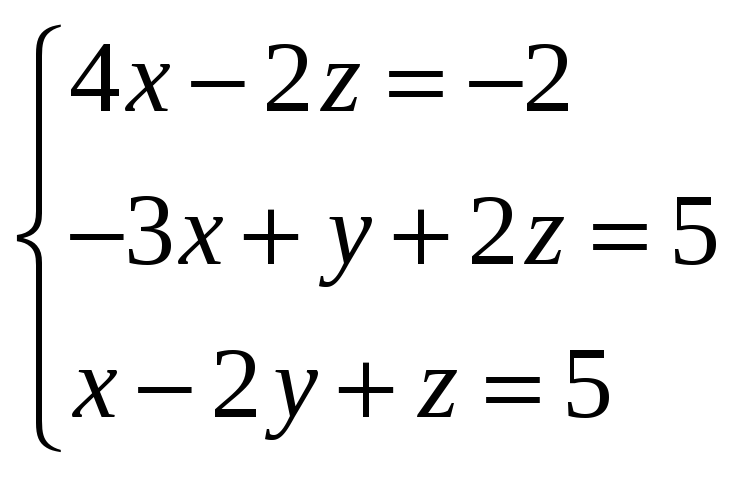
Для решения системы линейных уравнений воспользуемся методом Крамера.

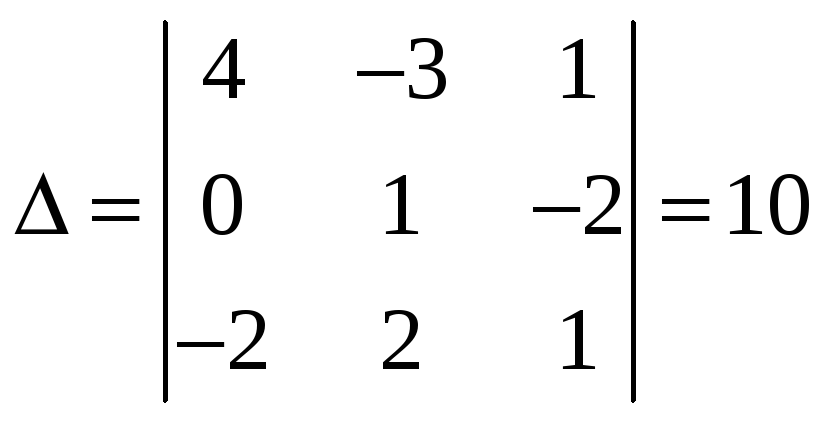
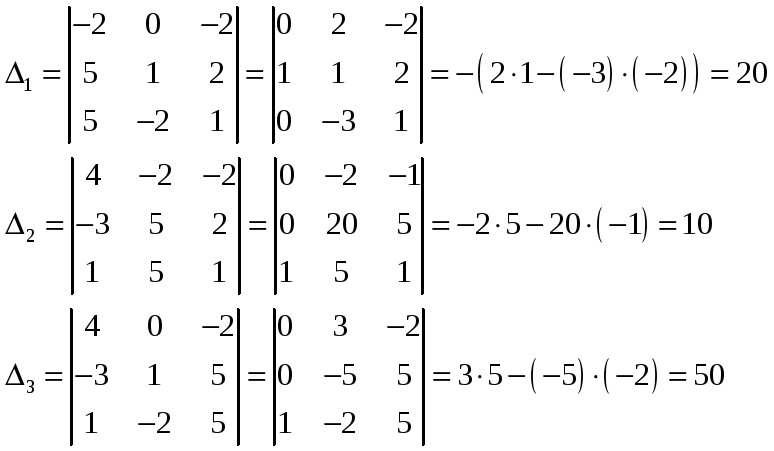
По формулам Крамера находим решение системы:

Таким образом, вектор в базисе векторов имеет вид:

Задачи 11–20

Даны координаты вершин пирамиды . Найти: 1) длину ребра ; 2) уравнение прямой ; 3) угол между рёбрами и ; 4) уравнение плоскости ; 5) угол между ребром и гранью ; 6) уравнение высоты, опущенной из вершины на грань ; 7) площадь грани ; 8) объём пирамиды; 9) сделать чертёж.

Задача 12: ; ; ; .

Решение:

1) Вычислим длину ребра А₁А₂.

Длина ребра численно равна расстоянию между точками и , которое в прямоугольной декартовой системе координат вычисляется по формуле

,

где координаты точки , координаты точки .

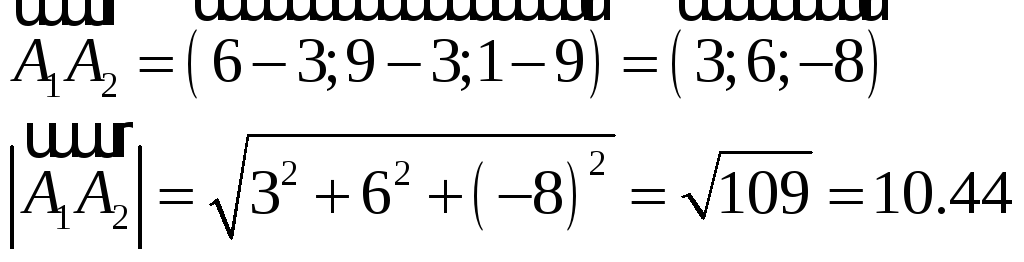
2)  Для составления уравнений прямой воспользуемся формулой: , где координаты точки , координаты точки . Тогда уравнение прямой будет иметь вид:

3) Найдем угол между ребрами А₁А₂ и А₁А₄

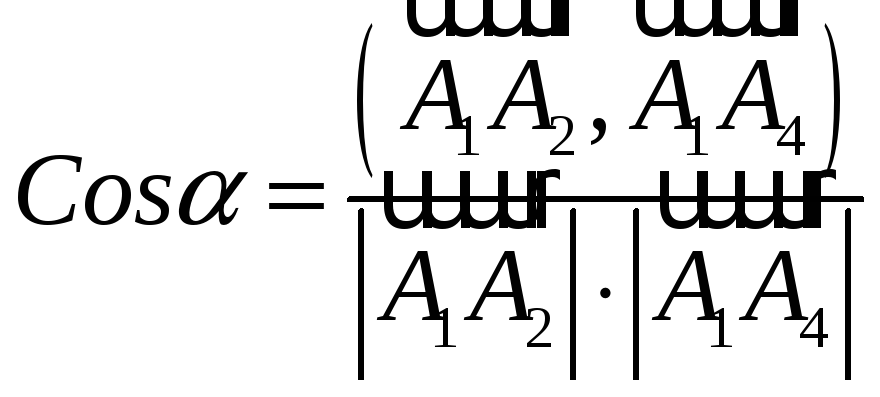
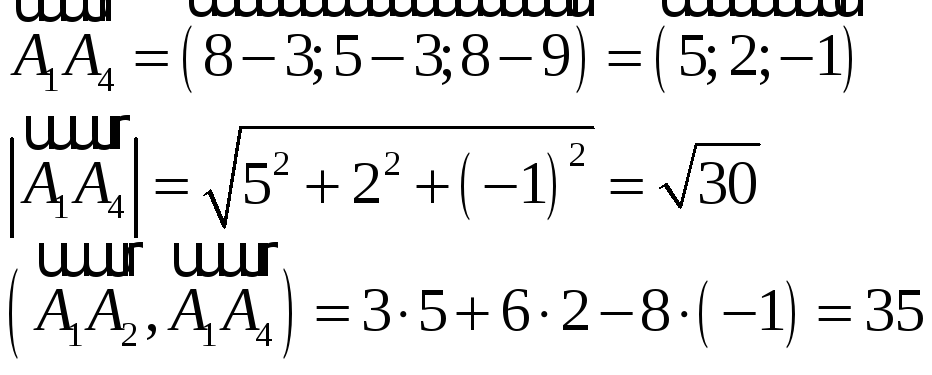
Таким образом,

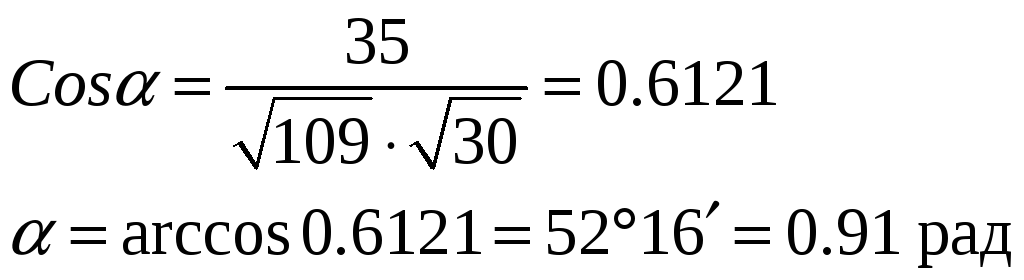
4) Составим уравнение плоскости

- нормаль искомой плоскости

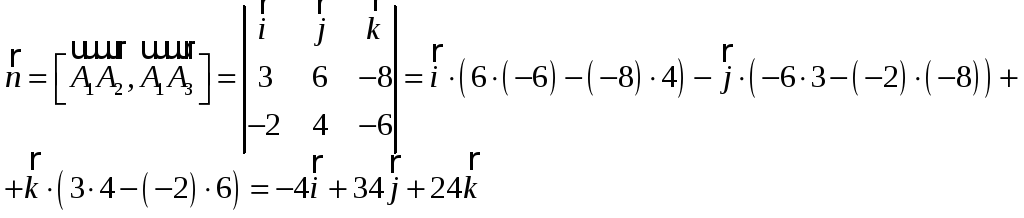
Таким образом, уравнение плоскости имеет вид:

_{-4x + 34 y +24z + с = 0}

_{2x – 17y – 12z + с = 0}

_{Для определения с подставим координаты точки А1 в уравнение.}

_{2 · 3 – 17 · 3 – 12 · 9 + с = 0}

_{– 153 + с = 0}

_{с = 153}

Таким образом, уравнение плоскости имеет вид:

_{2x – 17y – 12z + 153 = 0}

5) угол между ребром и гранью

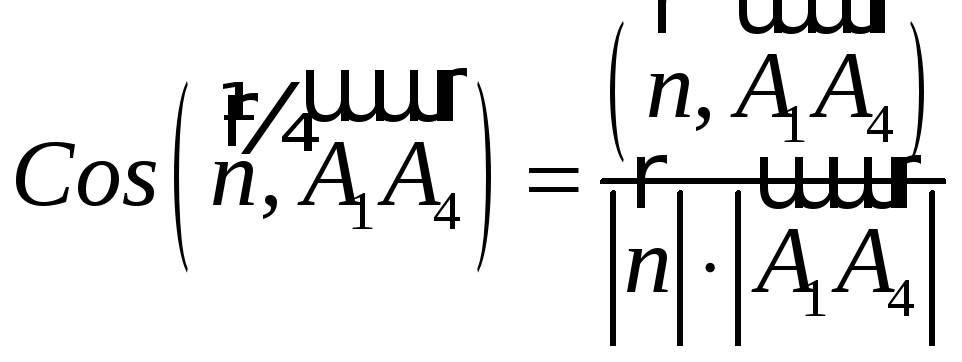
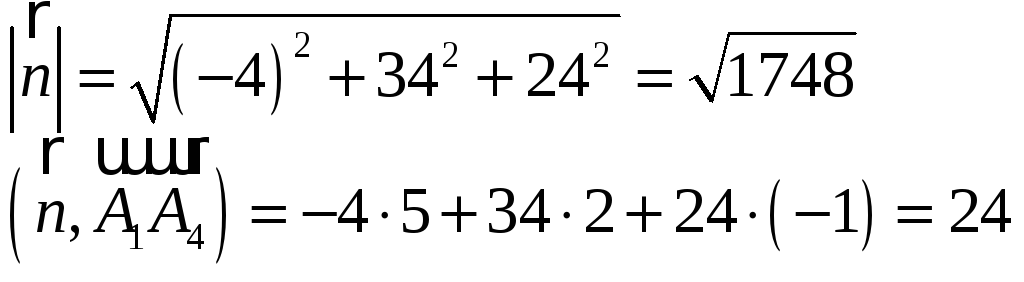
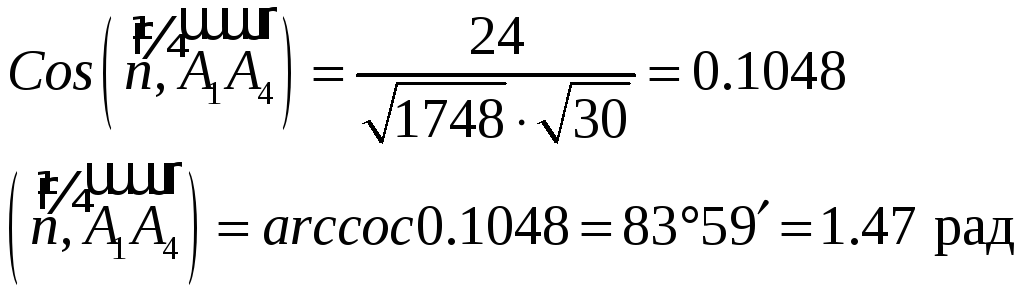
β – искомый угол между ребром и гранью

6) Искомое уравнение высоты получим из канонических уравнений прямой

,

где точка, лежащая на искомой прямой; координаты направляющего вектора , параллельного искомой прямой. При этом в качестве точки возьмем точку , из которой по условию задачи должна быть опущена высота на плоскость , а в качестве вектора возьмем нормальный вектор плоскости , т.е. . уравнение высоты, опущенной из вершины на грань

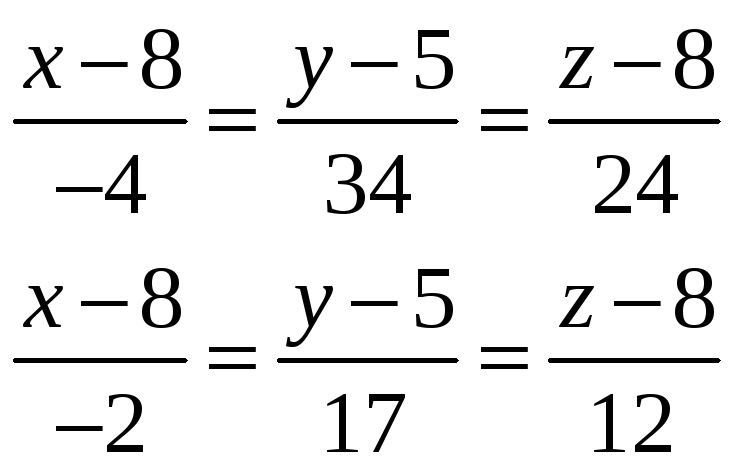
7) площадь грани А₁А₂А₃

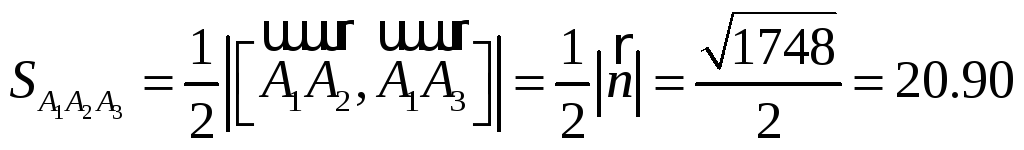
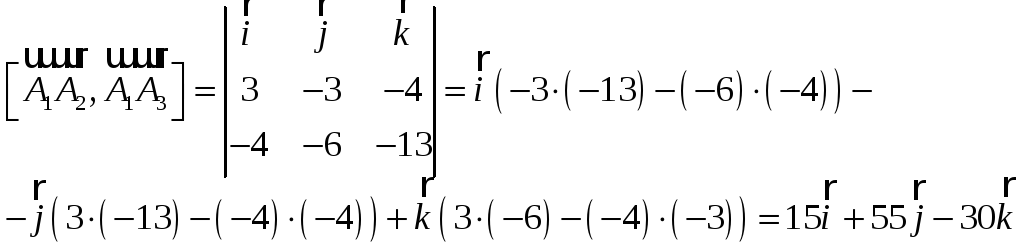
8) объем пирамиды

9) сделать чертёж

А1

А3

А2

z

y

x

А4

Задача 22. Найти координаты точки , симметричной точке относительно плоскости .

Решение:

Уравнение прямой, которая проходит через точку  перпендикулярно заданной плоскости будет:

.

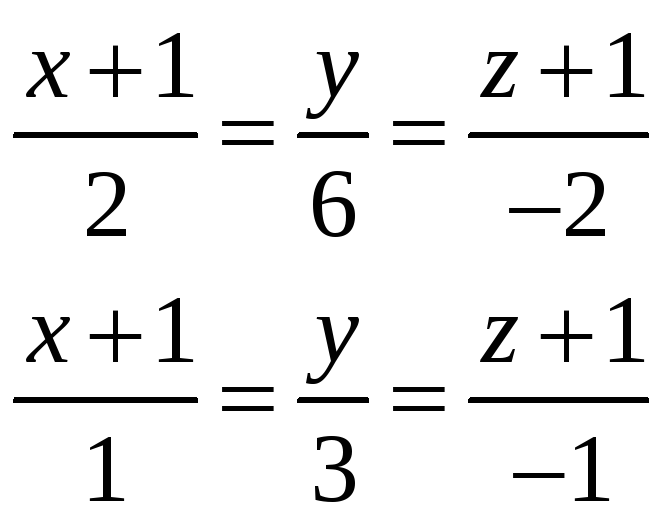Найдем точку пересечения прямой и плоскости.

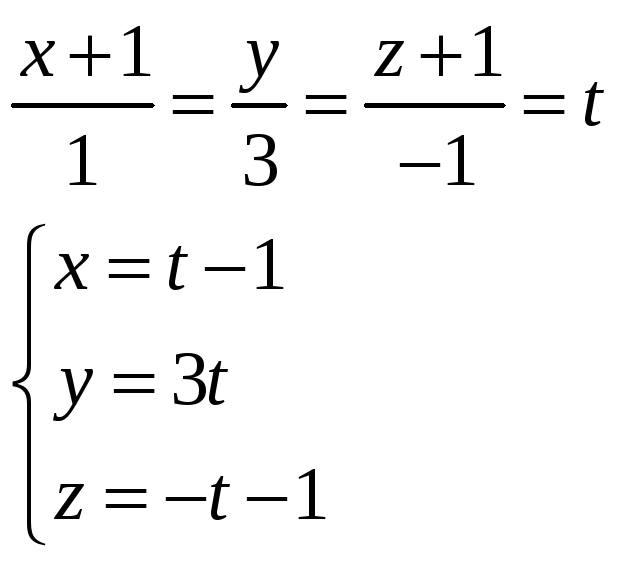
Подставим полученные выражения в уравнение заданной плоскости.

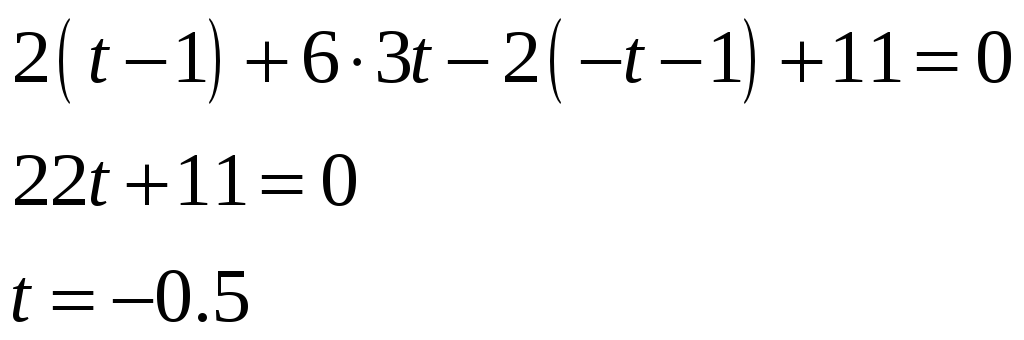
Откуда  – точка пересечения прямой и плоскости.  является серединой отрезка MM’, поэтому

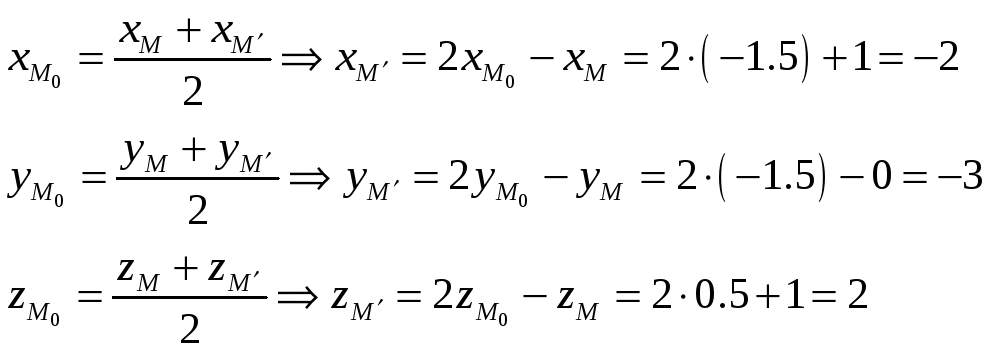
Т.е. .

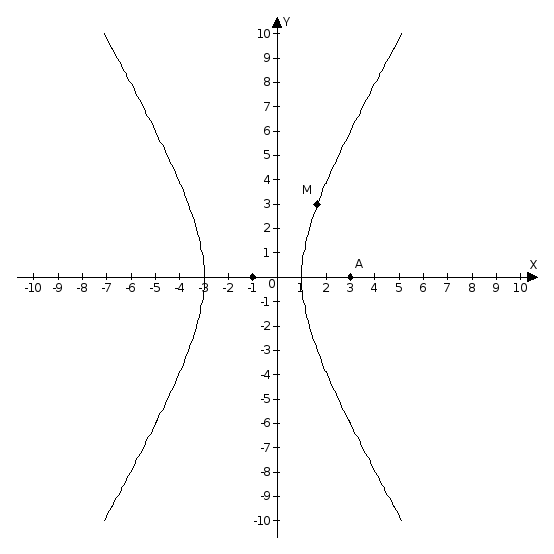
Задача 32. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки , чем от оси ординат. Привести полученное уравнение к каноническому виду и указать тип линии, описываемой этим уравнением.

Решение:

Обозначим произвольную точку искомой линии как . Тогда по условию получаем, что , где точка Р – основание перпендикуляра, опущенного из точки М на ось ординат.

Находим:

;

.

.

Значит,

.

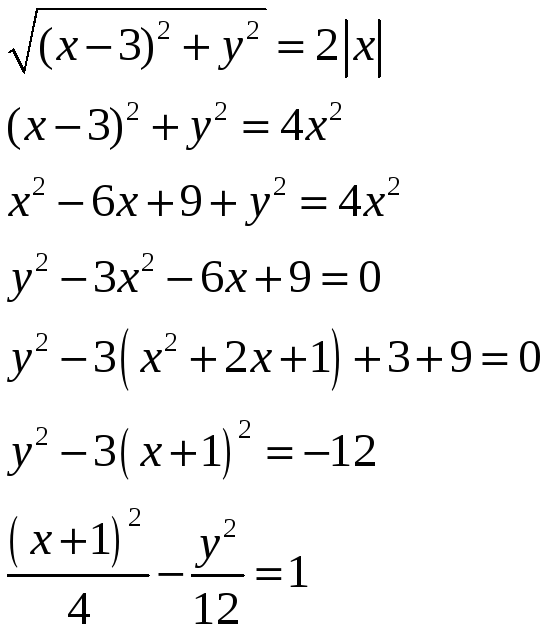Это каноническое уравнение гиперболы с полуосями и центром в точке (-1;0).

P

10