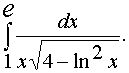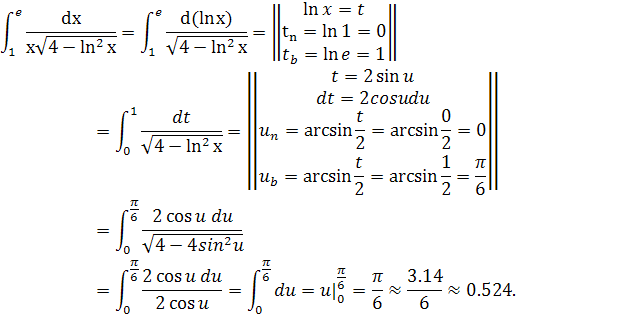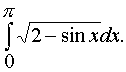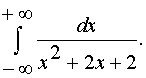Контрольная №6 вар 1
.docБелорусский Государственный Университет Информатики и Радиоэлектроники
Специальность:
Программное Обеспечение Информационных Технологий (ПОИТ)
Контрольная работа по математике №6
Вариант 1
Номер зачетной книжки 801021-21
Выполнил:
Мелещеня Валерий Сергеевич
№ 281 Найти неопределенные интегралы (результаты в случаях “а” и “б” проверить дифференцированием).
а)
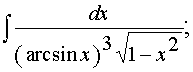 б)
б)
![]() в)
в)
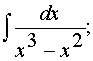
г)
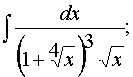 д)
д)
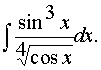
Решение:
а)
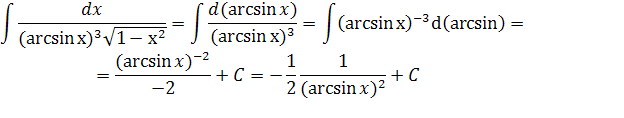
Проверка:

б)
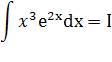
Интегрируем по частям:
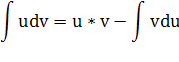
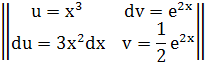
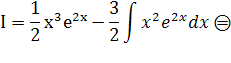
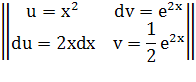
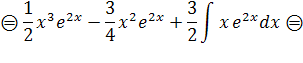
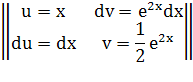
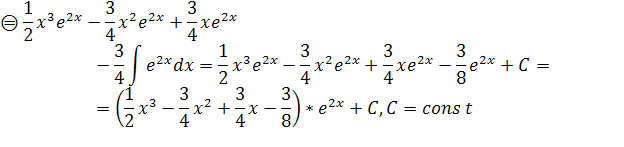
Проверка:
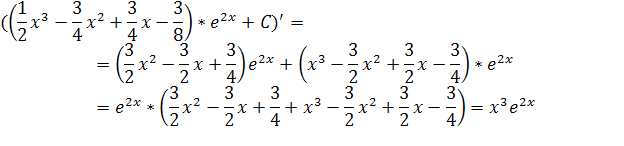
в)
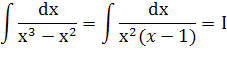
Разложим подынтегральную функцию на простейшие дроби.
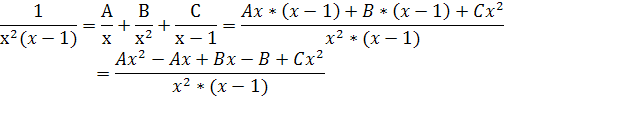
Для определения коэффициентов получим систему:
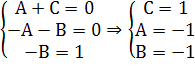
Тогда

г)
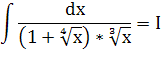
Имеем интеграл вида:
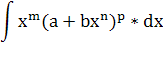
m=-![]() ;
p=-1;
n=
;
p=-1;
n=![]() p
p![]() z
z
Замена:
x=![]()
![]() =
=![]() (t=
(t=![]() )
)
![]()

Значит
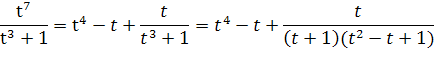
Последнюю дробь разложим на простейшие
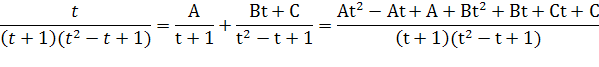
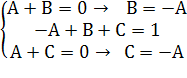
-A-A-A=1
-3A=1
A=-![]() ;
B=
;
B=![]() ;
C=
;
C=![]() ;
;
Получим:
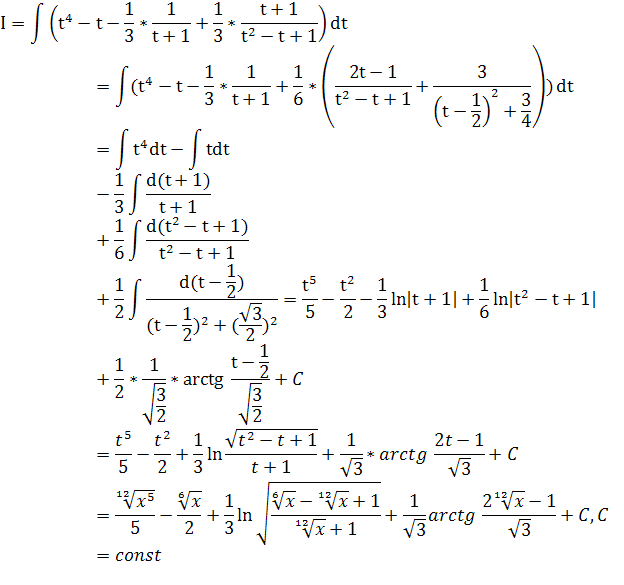
д)
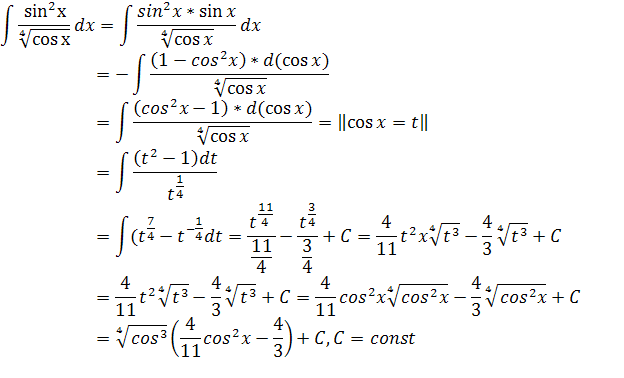
№ 291
Вычислить определенный интеграл. Окончательный результат представить в виде приближенного числа, произведя вычисление с округлением до третьего десятичного знака.
|
Решение:
№ 301 Вычислить интеграл с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
|
Решение:
Формула Симпсона:
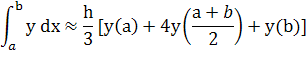
Где
h=![]()
Где
y(a),
y(b),
y(![]() )
– значение функции в соответствующих
точках.
)
– значение функции в соответствующих
точках.
Разобьем отрезок [0;π] на 10 частей и для каждой из них применим формулу.
Все вычисления занесём в таблицу:
|
Отрезок |
y(a) |
y(b) |
y((a+b)/2 |
4y(a+b)/2 |
h/3[y(a)+4y((a+b)/2)+y(b)] |
|
[0;π/10] |
1,414 |
1,3 |
1,358 |
5,431 |
0,426 |
|
[π/10;2π/10] |
1,3 |
1,188 |
1,243 |
4,974 |
0,391 |
|
[2π/10;3π/10] |
1,188 |
1,091 |
1,137 |
4,548 |
0,357 |
|
[3π/10;4π/10] |
1,091 |
1,024 |
1,053 |
4,212 |
0,331 |
|
[4π/10;5π/10] |
1,024 |
1 |
1,006 |
4,025 |
0,317 |
|
[5π/10;6π/10] |
1 |
1,014 |
1,006 |
4,025 |
0,317 |
|
[6π/10;7π/10] |
1,014 |
1,091 |
1,053 |
4,212 |
0,331 |
|
[7π/10;8π/10] |
1,091 |
1,188 |
1,137 |
4,548 |
0,357 |
|
[8π/10;9π/10] |
1,188 |
1,3 |
1,243 |
4,974 |
0,391 |
|
[9π/10;10π/10] |
1,3 |
1,414 |
1,358 |
5,431 |
0,426 |
h=![]() =
=![]() ≈0.157
≈0.157
Тогда
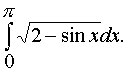 =(0,426+0,391+0,357+0,331+0,317)*2=3,644
– Ответ.
=(0,426+0,391+0,357+0,331+0,317)*2=3,644
– Ответ.
№ 311
Вычислить несобственный интеграл или доказать его расходимость.
|
|
Решение:
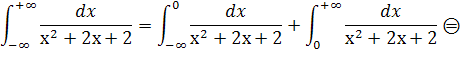
Согласно определению несобственного интеграла:
⊜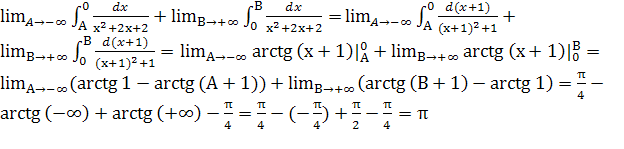 - Ответ.
- Ответ.
№ 321
Вычислить
площадь фигуры, ограниченной кривыми
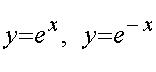 и
прямой х=1.
и
прямой х=1.
Решение:
Построим заданную фигуру:
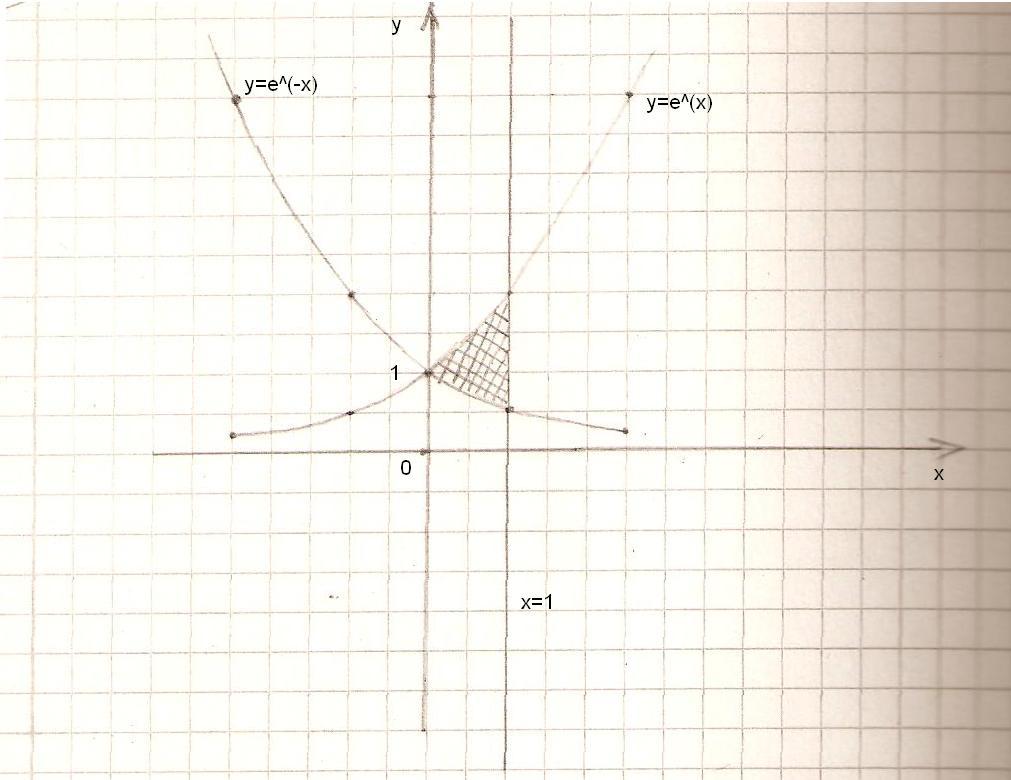
Площадь найдём по формуле:
S=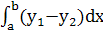 ,
где a=0,
b=1,
,
где a=0,
b=1,
![]()
S=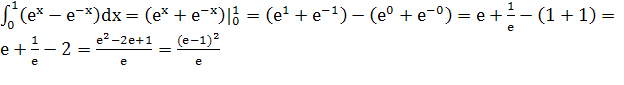 (квадратных единиц)
(квадратных единиц)
Ответ:![]() - (квадратных единиц)
- (квадратных единиц)
№ 331
Найти
координаты центра тяжести однородной
плоской фигуры, ограниченной дугой
эллипса
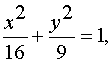 расположенной
в первой четверти, и осями координат.
расположенной
в первой четверти, и осями координат.
Решение:
Изобразим заданную фигуру:

Координаты центра тяжести:
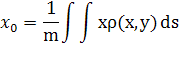
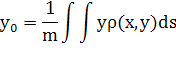
m=![]()
По
условию ![]()
Перейдём к обобщенным координатам:
x=4r
cos ![]() ds=r du dr
ds=r du dr
y=3r
sin ![]()
Тогда
S:
0![]()
![]()
Получаем:
m=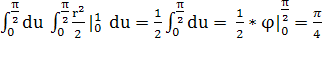
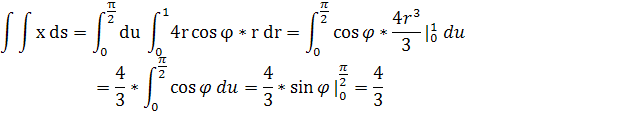
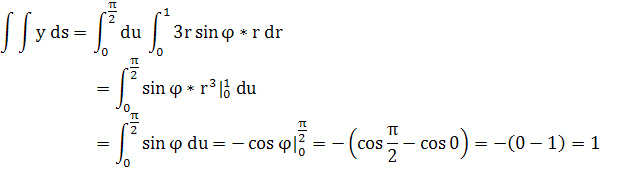
Значит:
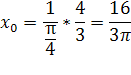
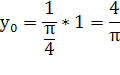
Ответ:
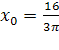
![]() =
=![]()