УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет непрерывного и дистанционного обучения

Специальность: программное обеспечение информационных технологий

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ №2

2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

60. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

Матрица системы равна

Вектор свободных членов:

Тогда расширенная матрица для решения методом Гаусса имеет вид:

Решим систему средствами матричного метода. Для этого необходимо вычислить обратную матрицу.

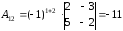
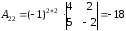
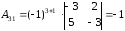
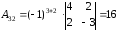
70. Найти размерность и базис пространства решений однородной системы линейных уравнений.

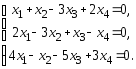
Решение. Находим ранг основной матрицы системы с помощью элементарных преобразований:

Так как ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы Преобразованная система, эквивалентная исходной, имеет вид

.

Эти формулы дают общее решение. В векторном виде его можно записать следующим образом

,

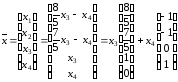где и - произвольные числа. Вектор-столбцы 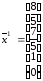и образуют базис пространства решений данной системы.

Полагая 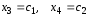, где - произвольные постоянные, получим общее решение в векторном виде .

80. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее через

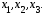
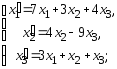
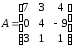Решение. Первое линейное преобразование имеет матрицу , второе имеет матрицу . Тогда произведение (т.е. последовательное выполнение) линейных преобразований имеет матрицу , т.е.

.

Поэтому искомое линейное преобразование имеет вид

.

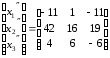
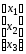90. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Составляем характеристическое уравнение матрицы

Корнями этого уравнения являются числа -2, 2, 8

.

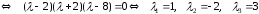При система (2.1) имеет вид

Таким образом, числу соответствует собственный вектор

,

где - произвольное действительное число. В частности, при имеем .

Аналогично для имеем

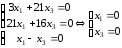
Откуда второй собственный вектор . При получаем собственный вектор .

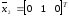Наконец, при 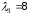решаем систему

, т.е. вектор .

В частности, при имеем .

Итак, матрица А имеет три собственных значения , , .

100. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.

Левая часть уравнения представляет собой квадратичную форму с матрицей . Решаем характеристическое уравнение

т.е. .

Находим собственные векторы из системы уравнений при

При система принимает вид

Получаем 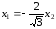, т.е. собственный вектор для .

При система принимает вид

Получаем , т.е. собственный вектор для .

Нормируем собственные векторы , получаем , . Составляем матрицу перехода от старого базиса к новому , в которой координаты нормированных собственных векторов записаны по столбцам. Выполняя преобразование

, получаем из исходного уравнения кривой

Последнее уравнение есть каноническое уравнение элипса.

11