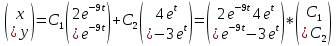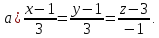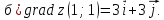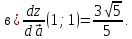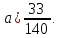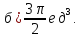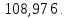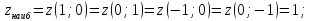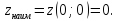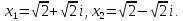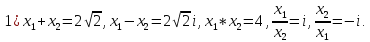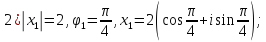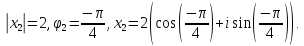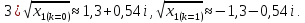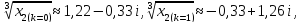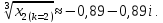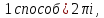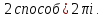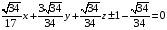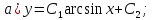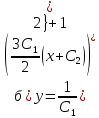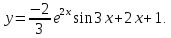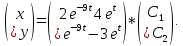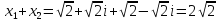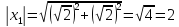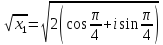КР №3 высшая математика 1 курс
.docxМинистерство образования республики Беларусь
Учреждение образования
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»
Институт информационных технологий
Специальность_________________________________
КОНТРОЛЬНАЯ РАБОТА №3
По курсу_____________________________________
Вариант №_____
Студент-заочник___ курса
Группы №______________
ФИО __________________
_______________________
Адрес__________________
_______________________
Тел. ___________________
Минск, 2010
Таблица ответов к задачам контрольной работы
|
Задача 1
|
Задача 2
|
|
Задача 3
|
|
|
Задача 4
|
|
|
Задача 5
|
|
|
Задача 6
|
|
|
Задача 7
|
Задача 8
|
|
Задача 9
|
Задача 10
|
Задача №1.
Написать
(а)
уравнение касательной плоскости и
нормали в точке (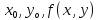 )
к поверхности S,
заданной уравнением
)
к поверхности S,
заданной уравнением
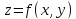 ;
Вычислить (б)
grad(z)
в точке
;
Вычислить (б)
grad(z)
в точке
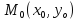 и (в)
производную функции
и (в)
производную функции
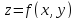 в точке
в точке
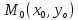 по направлению вектора
по направлению вектора
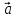 .
.
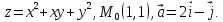
Решение:
а)
Найдем уравнение касательной плоскости
и нормали в точке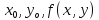 к поверхности S
по
формулам:
к поверхности S
по
формулам:
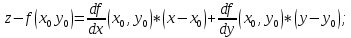
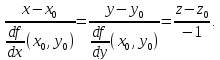
Найдем
частные производные функции
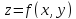 и их значения в точке
и их значения в точке
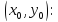
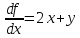
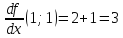
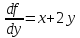
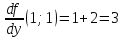
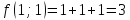
Тогда уравнение касательной плоскости примет вид:
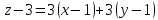
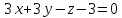
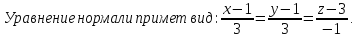
б)
Найдем grad z в точке
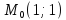 по формуле:
по формуле:
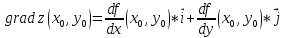
Получим:
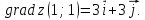
в)
Найдем производную функции z в точке
M0
по направлению вектора
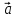 по формуле:
по формуле:
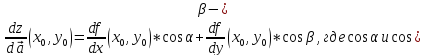
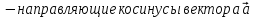
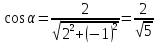
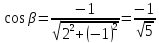
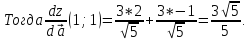
Задача №2.
Вычислить (а) двойной интеграл по облачти D, ограниченной
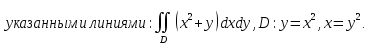
Вычислить (б) объем тела, ограниченного поверхностями:
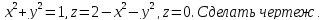
Решение:
а)
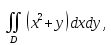
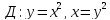
Найдем
координаты точек пересечения кривых
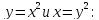
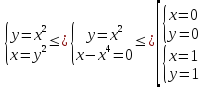
Сделаем чертеж области интегрирования Д:
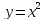
y

1
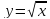
0
Пределы интегрирования примут вид:
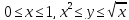
Перейдем
от двойного интеграла к двукратному по
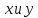 и вычислим его:
и вычислим его:
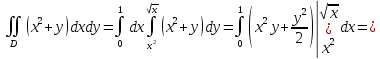
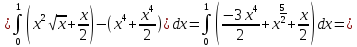
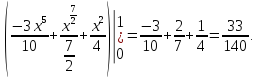
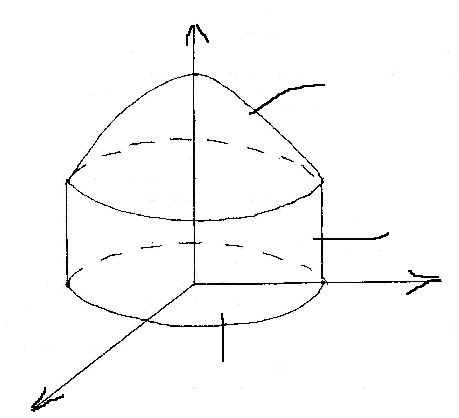
б) Сделаем чертеж тела, ограниченного указанными поверхностями:
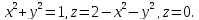
1
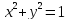
Z=0
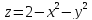
1
0
2
x
y
z
1
Вычислим объем тела при помощи тройного интеграла в цилиндрических координатах:
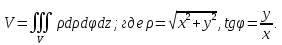
Проекция
тела
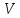 на плоскость
на плоскость
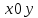 имеет вид:
имеет вид: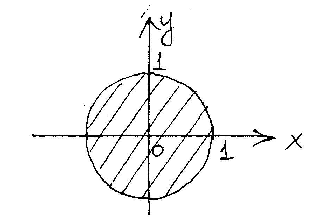
Пределы интегрирования имеют вид:
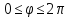
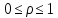
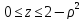
Получим:
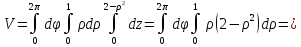
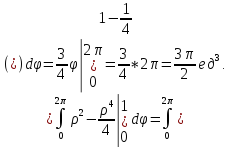
Задача №3.
Применяя формулу Тейлора для функции нескольких переменных вычислить значение 1,002*2,0032*3,0043. Использовать члены разложения до второго порядка включительно.
Решение:
Рассмотрим
функцию
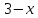 переменных:
переменных:
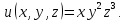
Воспользуемся
формулой Тейлора для функции
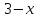 переменных 2го порядка для приближенного
нахождения значения функции при:
переменных 2го порядка для приближенного
нахождения значения функции при:
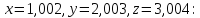
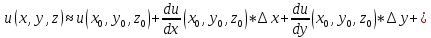
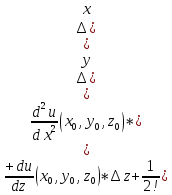
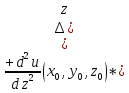
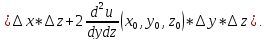
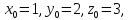
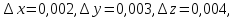
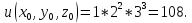
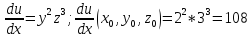
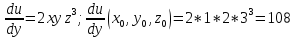
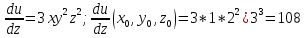
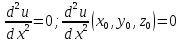
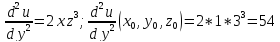
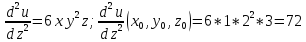
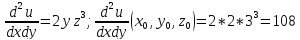
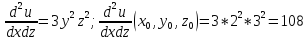
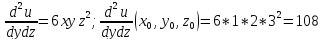
Тогда:
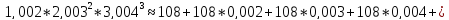
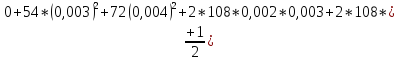
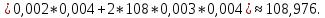
Задача №4.
Найти
наименьшее и наибольшее значения функции
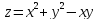
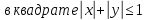 .
.
Решение:
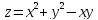
Д:
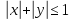 .
.
Сделаем чертеж области Д:

Найдем
частные производные 1го порядка функции
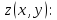
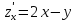
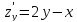
Найдем стационарные точки функции:
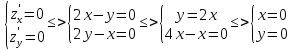
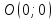 -
стационарная точка,
-
стационарная точка,
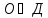
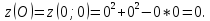
Исследуем
функцию
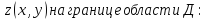
-
AB:
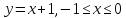
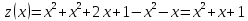
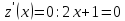
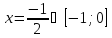
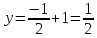
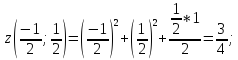
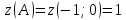
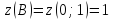
-
BC:
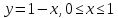
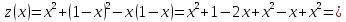
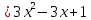
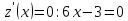
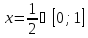
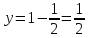
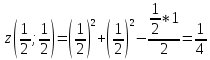
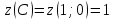
-
CD:
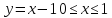
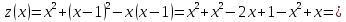
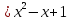
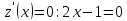
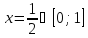
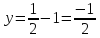
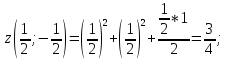
-
AD:
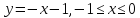

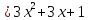
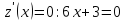
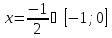
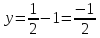
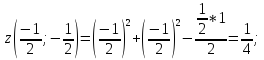
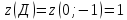
Так как
функция
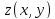 может принимать наибольшее и наименьшее
значения в области Д либо в стационарных
точках внутри области Д, либо на ее
границе, то выберем наибольшее и
наименьшее значения функции среди
найденных:
может принимать наибольшее и наименьшее
значения в области Д либо в стационарных
точках внутри области Д, либо на ее
границе, то выберем наибольшее и
наименьшее значения функции среди
найденных:
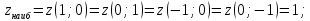
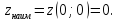
Задача №5.
Для
уравнеия
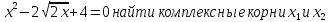 .
(За
.
(За
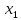 принять корень с положительной мнимой
частью.) Для них вычислить:
принять корень с положительной мнимой
частью.) Для них вычислить:
-
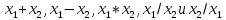 ,
, -
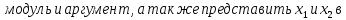
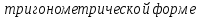 ,
,
-
все значения
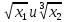 .
.
Решение:
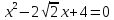
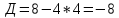
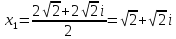
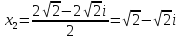
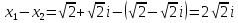
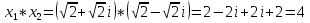
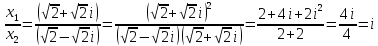
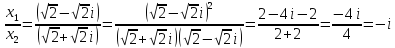
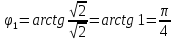
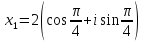
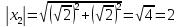
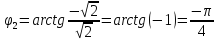
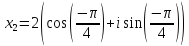
Воспользуемся формулой:
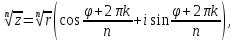
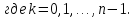
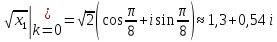
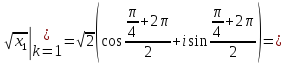
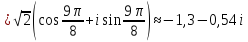
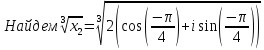
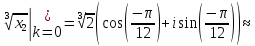
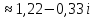
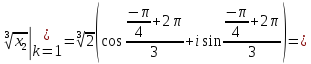
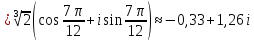
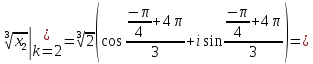
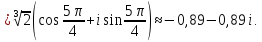
Задача №6.
Рассчитать
интеграл от функции
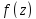 комплексного переменного
комплексного переменного
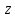 по пути
по пути
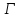 как криволинейный. Результат проверить
с помощью интегральной формулы Коши
или подсчета суммы вычетов.
как криволинейный. Результат проверить
с помощью интегральной формулы Коши
или подсчета суммы вычетов.
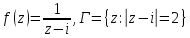
Решение:
1 способ
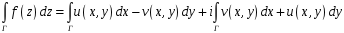
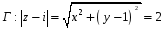
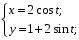
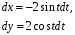
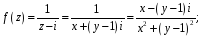
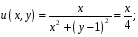
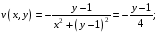
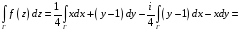

2 способ
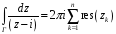
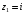 - полюс первого
порядка;
- полюс первого
порядка;
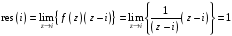
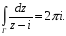
Задача №7.
Поверхность
задана параметризацией
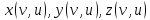 Найти на этой поверхности точки, в
которых касательная плоскость параллельна
плоскости
Найти на этой поверхности точки, в
которых касательная плоскость параллельна
плоскости
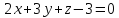 .
В ответ записать уравнения касательных
плоскостей в этих точках.
.
В ответ записать уравнения касательных
плоскостей в этих точках.
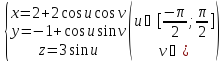
Решение:
Перейдем к новым координатам
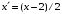 ,
,
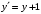
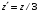 .
.
В новых координатах плоскость будет иметь вид
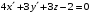 .
.
А радиус вектор поверхности:
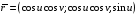 .
.
Нетрудно видеть, что в новых координатах мы получаем единичную сферу, неявное уравнение которой имеет вид
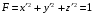 .
.
Нормаль к сфере имеет вид:
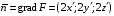 .
.
С учетом того, что
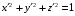 ,
уравнение единичной нормали будет иметь
вид:
,
уравнение единичной нормали будет иметь
вид:
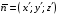 .
.
Для того, чтобы
касательная плоскость к поверхности
была параллельна заданной плоскости,
очевидно необходимо, что
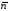 был коллинеарен вектору
был коллинеарен вектору
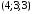 .
.
Таким образом, получим:
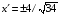 ,
,
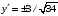 ,
,
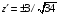 .
.
Эти значения определяют одновременно и компоненты нормали к сфере, и точки на сфере в которых выполняется требуемое условие.
Т.е. существует две касательные плоскости, параллельные данной (это понятно и из геометрических соображений). Уравнения этих плоскостей легко найти, зная их нормали, и точки через которые они проходят:
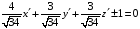 .
.
Или, возвращаясь к старым координатам
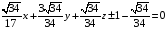 .
.
Задача №8.
Найти общее решение дифференциальных уравнений
(а)
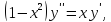 (б)
(б)
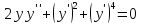 .
.
Решение:
(а)
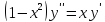
Это
дифференциальное уравнение 2го порядка,
не содержащее явным образом искомой
функции
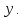
Пусть
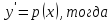
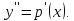 Уравнение
примет вид:
Уравнение
примет вид:


Разделяя переменные и интегрируя обе части уравнения, получим:
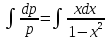
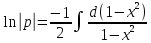
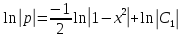
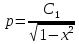
Учитывая,
что
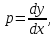 получим:
получим:

Разделяя переменные и интегрируя обе части уравнения, получим:
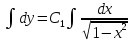
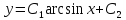 -
общее решение искомого уравнения.
-
общее решение искомого уравнения.
б)
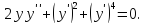
Это
дифференциальное уравнение 2го порядка,
не содержащее независимой переменной
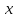 .
.
Пусть
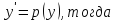
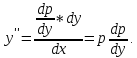
Уравнение примет вид:
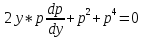
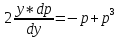
Разделяя переменные и интегрируя обе части уравнения, получим:
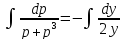
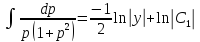
Представим
дробь
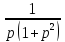 в виде суммы простейших дробей:
в виде суммы простейших дробей:
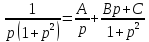
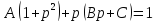
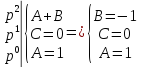
Тогда:
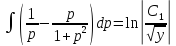
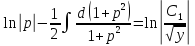
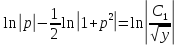
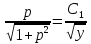
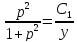
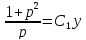
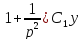
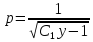
Учитывая,
что
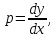 получим:
получим:
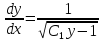
Разделяя переменные и интегрируя обе части уравнения, получим:
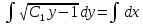
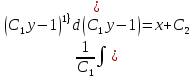
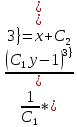
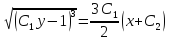

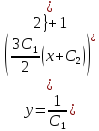
Задача №9.
Найти частное решение дифференциального уравнения
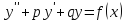 ,
удовлетворяющее условиям:
,
удовлетворяющее условиям:
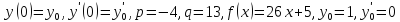
Решение:
Имеем линейное неоднородное дифференциальное уравнение с постоянными коэффициентами. Его общее решение найдем по формуле:
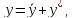
Где
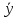 – общеерешение однородного уравнения,
– общеерешение однородного уравнения,
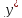 - частное
решение неоднородного уравнения.
- частное
решение неоднородного уравнения.
Составим характеристическое уравнение:
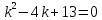
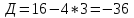
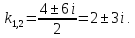
Тогда:
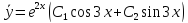
Будем
искать
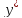 в виде:
в виде:
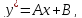
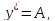
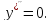
Подставим
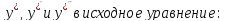
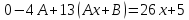
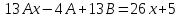
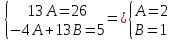
Тогда:
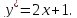
Общее решение имеет вид:
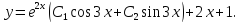
Найдем
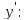
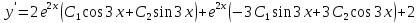
Воспользуемся данными начальными условиями:
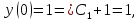
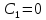
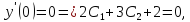
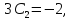
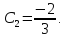
Тогда частное решение примет вид:
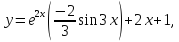
Или
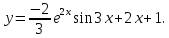
Задача №10.
С помощью характеристического уравнения найти общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами. Представить данную систему и ее решение в матричном виде.
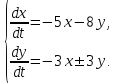
Решение:
Запишем систему в матричной форме:
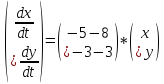
Будем искать частное решение в виде
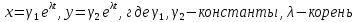
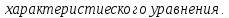
Составим характеристическое уравнеие матрицы системы:
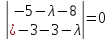
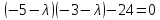
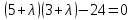
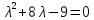
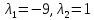
Находим
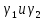 из системы уравнений:
из системы уравнений:
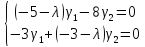
При
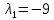 получим
получим
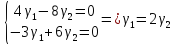
Пусть
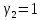 ,
тогда
,
тогда
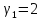
Таким
образом, характеристическому числу
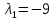 соответствует частное решение
соответствует частное решение
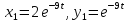
При
 получим:
получим:
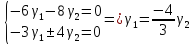
Пусть
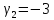 ,
тогда
,
тогда
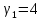
Характеристическому
числу
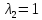 соответствует частное решение:
соответствует частное решение:
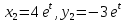
Общее решение системы находим как линейную комбинацию полученных частных решений, т.е.:
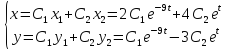
Или в матричной форме: