
Контрольная по ВМ №8, вариант 5
..doc
385.
Вычислить криволинейный интеграл
![]() вдоль
треугольника с вершинами А(-2, 0),
вдоль
треугольника с вершинами А(-2, 0),
В (2, 0), D (0, 2), обходя его против хода часовой стрелки.
Решение:
![]() ;
;
AB:
![]() ;
;
![]()
BD:
![]() ;
;
![]() .
.
DA:
![]() ;
;
![]() .
.
Таким образом
![]() .
.
395. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными
поверхностями. Данное тело и его проекцию на плоскость хОу изобразить на чертежах.
![]() .
.
Решение:
![]() .
.
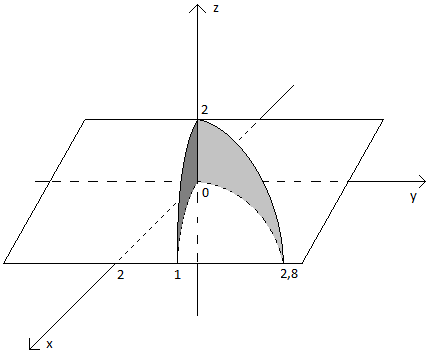
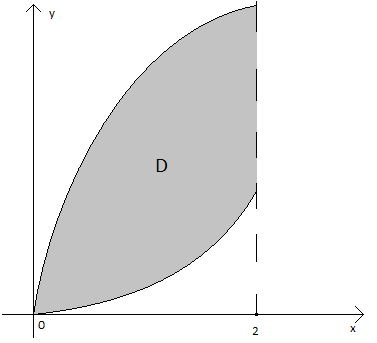
Область
D в плоскости xOy
есть
область, ограниченная снизу кривой
![]() ,
,
сверху
кривой
![]() и
справа прямой
и
справа прямой
![]() ( при
( при
![]() имеем
имеем![]() ),
),
х
изменяется от 0 до 2, у
изменяется от нижней кривой
![]() до
верхней
до
верхней
![]() ,
Поэтому, расставив пределы интегрирования,
получим
,
Поэтому, расставив пределы интегрирования,
получим
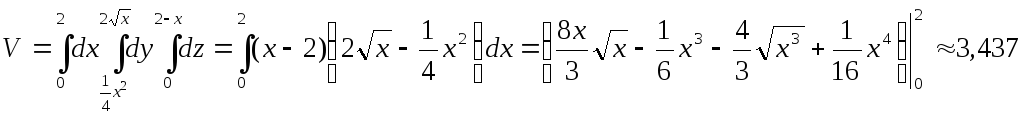 .
.
405. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры,
ограниченной
кривой
![]() ,
заданной уравнением в декартовых
координатах.
,
заданной уравнением в декартовых
координатах.
Параметр а положителен.
Решение:
В полярных координатах
![]() ,
поэтому
,
поэтому
![]() ;
;
![]() ,
так как
,
так как
![]() .
.
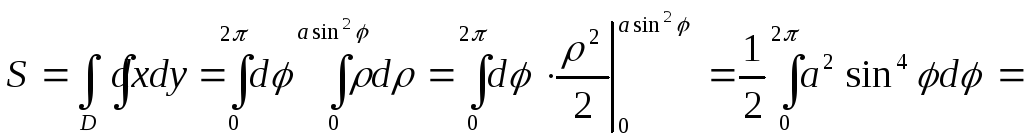
![]() (кв. ед.)
(кв. ед.)
415. Найти массу тела, ограниченного координатными плоскостями и плоскостью х + у + z = 1,
если плотность в каждой точке численно равна произведению координат этой точки.
Решение:
Пусть Т – поверхность ограниченная координатными плоскостями и плоскостью х + у + z = 1.
Плотность тела
![]() .
.
Тогда масса тела
![]()
![]()
![]()
![]() .
.
