Вышка 1 сем КР1 в2

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет непрерывного и дистанционного обучения

Специальность:

«Автоматизированные системы обработки информации»

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ №1

Вариант №2

Элементы векторной алгебры и аналитической геометрии.

Литература: [1], гл.1, § 1–3, гл. 2, 3, § 1-3; §[2], гл. 1, § 1–3;

[5], ч.1, § 1.1 – 1.5; [7] гл.4, 7, 9; 1 [7] ч.1.

Основные теоретические сведения

1. Базисом пространства называется совокупность линейно независимых векторов, по которым можно разложить любой вектор этого пространства.

Если векторы образуют базис, то любой вектор можно представить в виде

(1.1)

При этом числа и называются координатами вектора в базисе и определяются однозначно. Если известны координаты векторов и в некотором базисе, то из (1.1) может быть получена система трех уравнений с тремя неизвестными , . Для нахождения , такая система может быть решена по правилу Крамера

где определитель системы

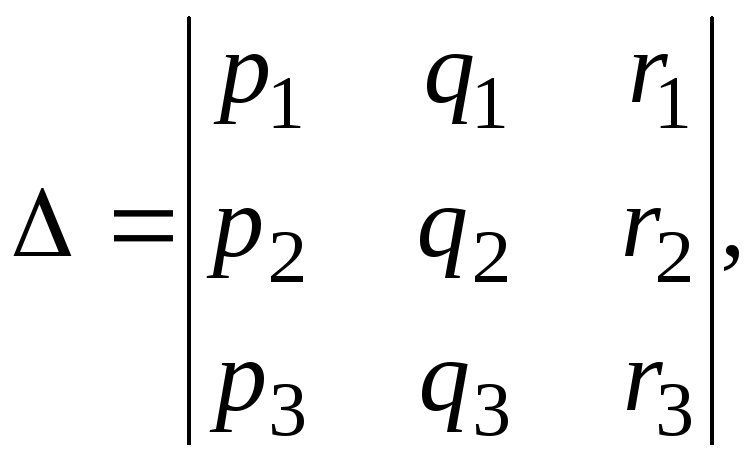
, а - определители, полученные из основного определителя заменой 1-го, 2-го, 3-го столбца соответственно столбцом из координат вектора .

2.1. Скалярным произведением двух векторов и называется число, определяемое равенством

где - угол между векторами и .

При этом длина вектора определяется по формуле

. (1.2)

2.2. Векторным произведением двух векторов и называется вектор , который направлен перпендикулярно векторам и так, что векторы , , образуют правую тройку, и длина вектора равна

Геометрически равен площади S параллелограмма, построенного на векторах

и .

В координатной форме

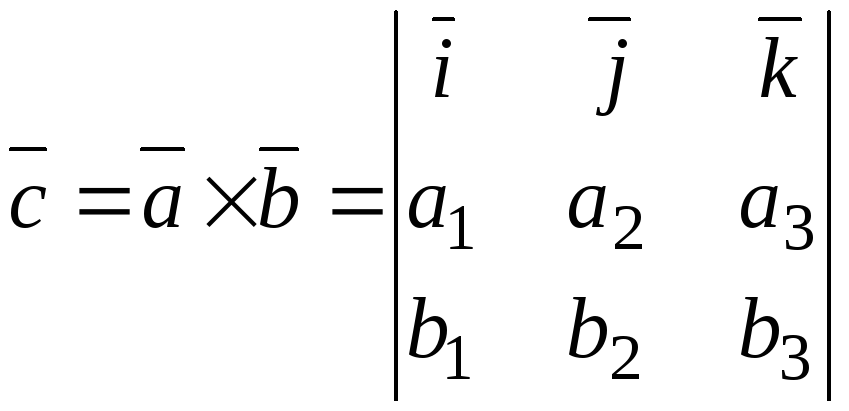. (1.3)

2.3. Смешанное произведение трех векторов

, , есть число, равное

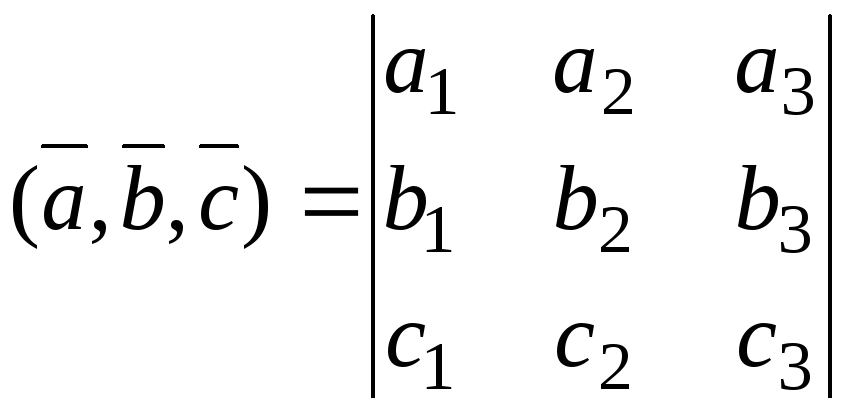. (1.4)

Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах , , .

2.4. Общее уравнение плоскости Р имеет вид

где - вектор, нормальный (перпендикулярный) плоскости (рис.2).

Уравнение плоскости, проходящей через точку перпендикулярно вектору , записывается в виде

. (1.5)

Угол  между двумя плоскостями с нормальными векторами и определяется по формуле .

Уравнение плоскости, проходящей через три заданные точки , , , имеет вид

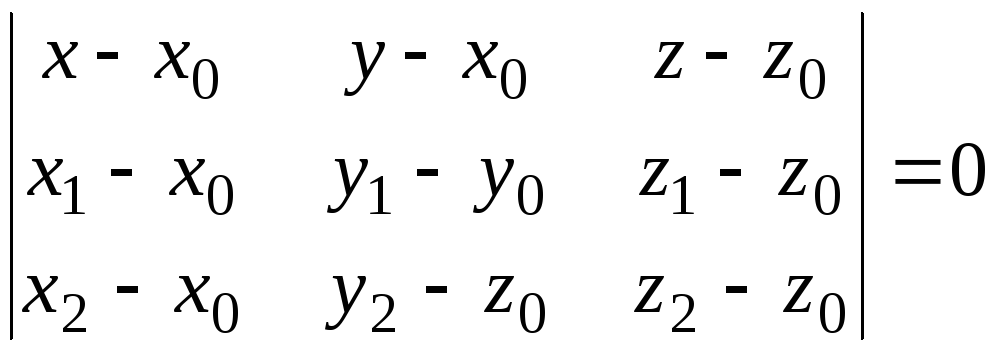. (1.6)

2.5. Уравнение прямой в пространстве, проходящей через две заданные точки и , имеет вид

. (1.7)

3. Уравнение прямой на плоскости в виде называется уравнением с угловым коэффициентом k. Если две прямые перпендикулярны, то произведение их угловых коэффициентов равно –1, т.е. ; если они параллельны, то .

Уравнение прямой с угловым коэффициентом k, проходящей через точку , имеет вид .

4. Пусть L – некоторая линия, каждая точка М которой обладает следующим свойством: отношение расстояний от точек L до данной точки F и до данной прямой (d) равно числу , т.е. . Число  называется эксцентриситетом. Если  < 1, то множество точек L определяет эллипс: .

Если  > 1, то L – гипербола: .

Если  = 1, то L – парабола: .

Решение практических задач

2. Даны четыре вектора (а₁, а₂, а₃), (b₁, b₂, b₃), (c₁, c₂, c₃) и (d₁, d₂, d₃) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.

(3,-5,2), (4,5,1), (-3,0,-4), (-4,5,-16).

Решение. Чтобы проверить, что система векторов образует базис, надо найти ее ранг. Для пространства V3 ранг системы векторов должен равняться 3.

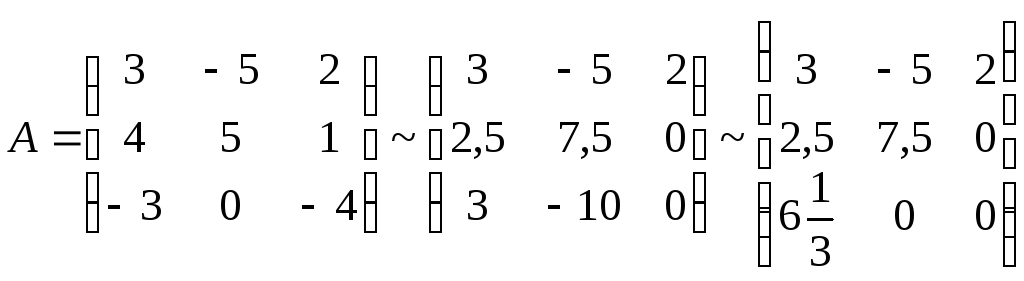
rang(A)=3.

Следовательно, тройка векторов является базисом.

Составим систему уравнений (1.1) в координатном виде 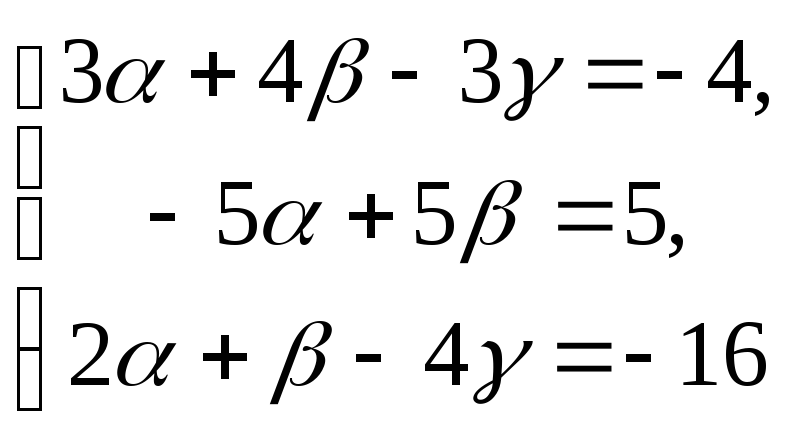и найдем . Определитель найден выше и = -95.

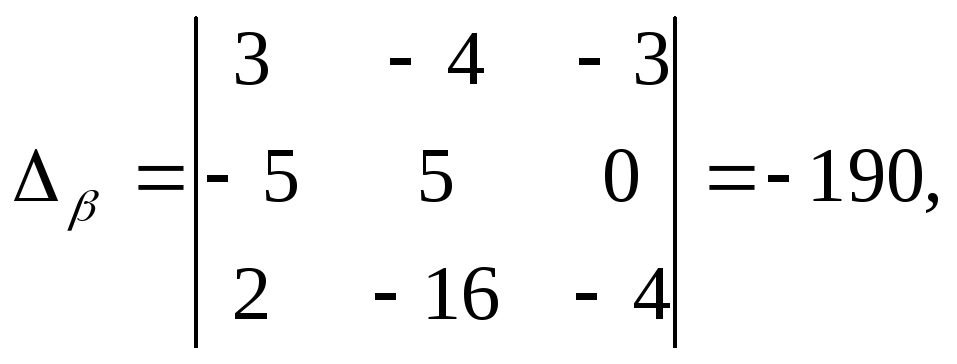
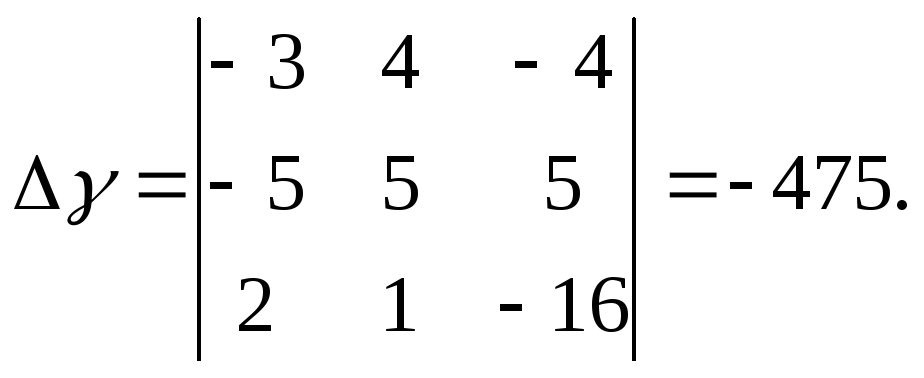
Имеем ; ; .

Значит, .

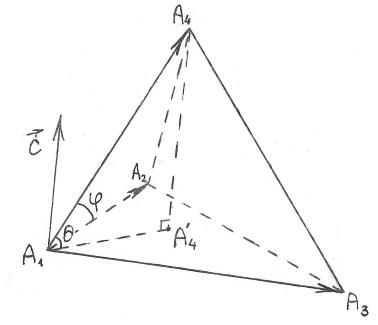
12. Даны координаты вершин пирамиды A₁A₂A₃A₄. Найти: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃; 4) площадь грани А₁А₂А₃; 5) объём пирамиды; 6) уравнения прямой А₁А₂; 7) уравнение плоскости А₁А₂А₃; 8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертёж.

А₁(3,3,9), А₂(6,9,1), А₃(1,7,3), А₄(8,5,8).

Решение. 1. Находим координаты вектора . Длина ребра А₁А₂ равна модулю вектора и вычисляется следующим образом:

по формуле (1.2).

2. Угол  между ребрами и вычисляется по формуле из скалярного произведения. , ;. Поэтому ,

3. Угол между ребром и плоскостью - это угол между вектором и его ортогональной проекцией на грань .

Вектор перпендикулярен грани , что вытекает из определения векторного произведения векторов и (1.3):

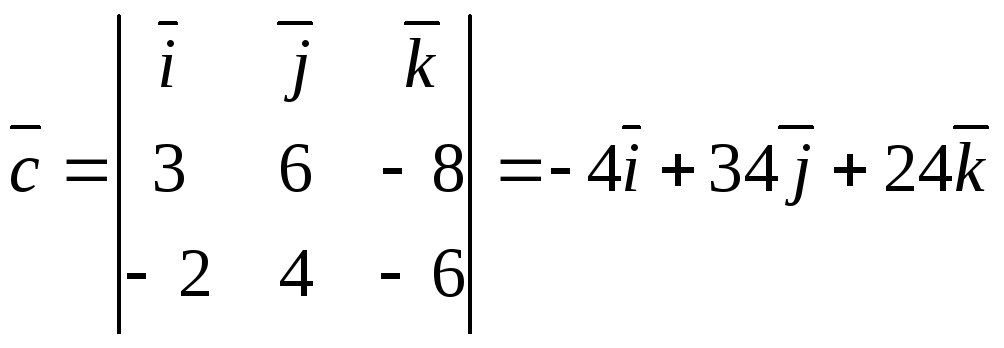. (Здесь . Как и в предыдущем пункте, находим ,

.

4. Площадь грани находим, используя геометрический смысл векторного произведения

.

5. Объем пирамиды численно равен одной шестой модуля смешанного произведения векторов , , (формула 1.4).

.

6. Для составления уравнений прямой воспользуемся формулой (1.7), где - координаты точки , - координаты точки .

.

В таком виде уравнения прямой называются каноническими. Они могут быть записаны и в виде

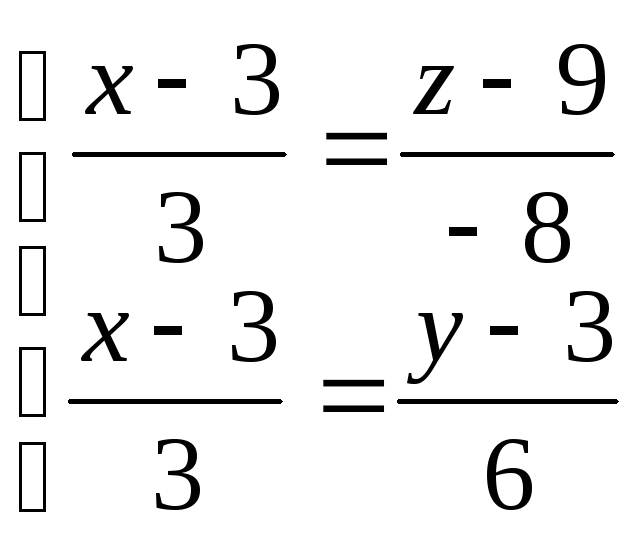или , т.е. уравнение прямой как линии пересечения двух плоскостей.

7. Для составления уравнения плоскости воспользуемся формулой (1.6), где - координаты , - координаты , - координаты .

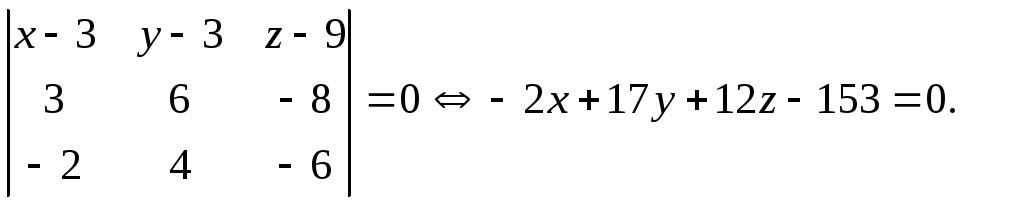
8. Искомые уравнения высоты получим из канонических уравнений прямой , где - точка, лежащая на искомой прямой,; - координаты вектора , параллельного искомой прямой. При этом в качестве точки возьмем точку , а в качестве вектора возьмем нормальный вектор плоскости , т.е. . Имеем .

9. Сделаем чертеж

22. На прямой 2x+y+11=0 (1) найти точку, равноудалённую от двух данных точек A(1,1) и B(3,0).

Решение. Геометрическое место точек, равноудаленных от точек А и В – посрединный перпендикуляр к отрезку АВ. Найдем уравнение прямой АВ:

АВ:

Вектор, нормальный к прямой АВ - . Точка С – середина отрезка АВ имеет координаты С (2; 0,5). Тогда прямая, содержащая посрединный перпендикуляр к отрезку АВ задается с помощью точки С и направляющего вектора :

(2)

Найдем точку пересечения прямых (1) и (2):

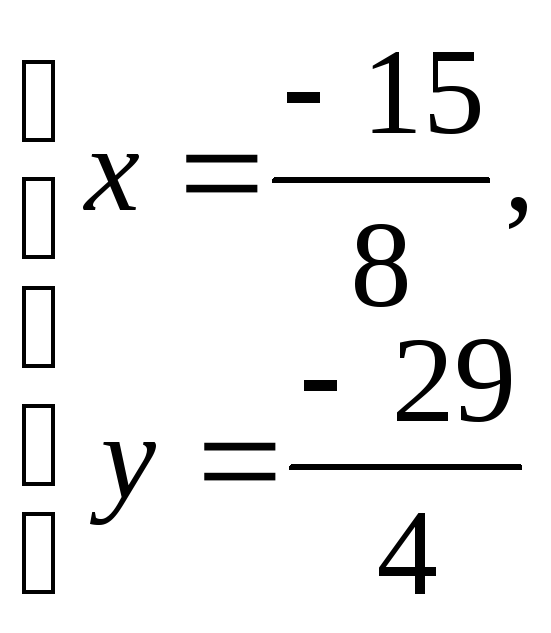
Таким образом, на прямой 2x+y+11=0 равноудалённой от двух данных точек A(1,1) и B(3,0) является точка с координатами (;).

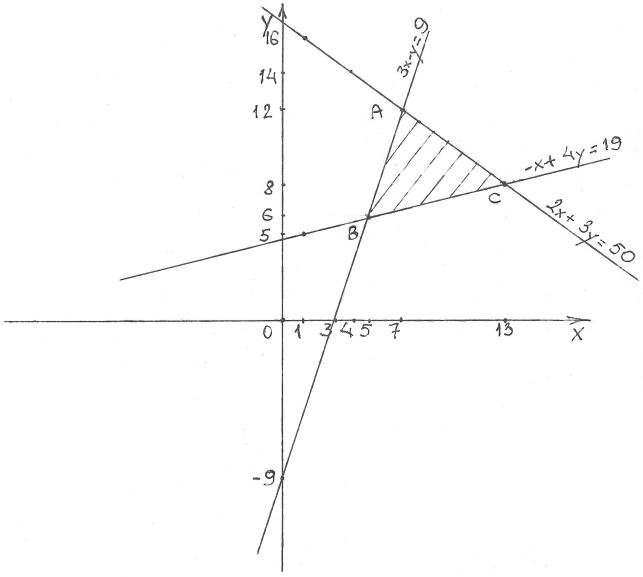
32. Построить на плоскости область решений системы линейных неравенств

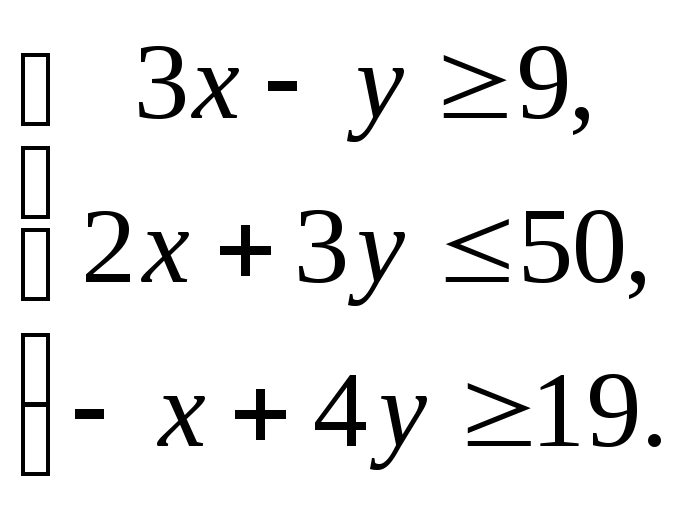
Решение. Чтобы решить неравенство , рассмотрим прямую . Она проходит через две точки и . При

неравенство является неверным. Следовательно, ему удовлетворяют все точки, лежащие ниже прямой и на прямой.

Для решения второго неравенства строим прямую , проходящую через точки и . Точка удовлетворяет неравенству , следовательно, ему удовлетворяют все точки, лежащие ниже прямой и на этой прямой. Находим точку А пересечения прямых и , решая систему

.

Наконец, решаем неравенство . Для этого строим прямую , проходящую через точки и . Точка (0;0) не удовлетворяет этому неравенству, поэтому его решением является множество точек плоскости выше прямой и на самой прямой.

Решая системы уравнений

и , находим координаты точек и . Данной системе неравенств удовлетворяют все точки внутри треугольника АВС и на его границе.

42. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки A(3,0), чем от оси ординат.

Решение. Обозначим произвольную точку искомой линии . Тогда по условию , где Р - основание перпендикуляра из точки М к оси ординат. Но . Значит, . Возводя в квадрат, получаем Это каноническое уравнение гиперболы с действительной полуосью и мнимой полуосью и центром – (-1;0).