КР №3 по вышке 2 вариант

Агаджанов Владимир Леонидович

Факультет: З и Д О

Курс:1

Вариант:2

Контрольная работа по высшей математике

Контрольная работа №3

Тема 3. ВВЕДЕНИЕ В АНАЛИЗ

102. Построить график функции преобразованием графика функции .

Дано:

Решение. Так как график функции известен, это синусоида. То построение графика функции заключаться в четырех этапах преобразование графика функции . Представим заданную функцию, как y = - Asin(bx+c).

1.Постоим график y = sin bx, где b = 2 что показывает сжатие графика функции в два раза.

2. Построим график y = sin(2x+c), где c = 3, что показывает смещение графика функции y = sin(2x+c), по оси Ох в минусовую сторону

3. Построим график y = A sin(2x+3), где A = 3, что показывает растяжение графика функции у = sin(2x+3), в 3 раза по оси Oy.

4. Построим график функции y = - A sin(2x+3) путем зеркального отображения графика функции y = A sin(2x+3) относительно оси Ox

112. Дана функция на отрезке . Требуется: 1) построить график функции в полярной системе координат по точкам, давая  значения через промежуток  /8, начиная от  =0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс с полярной осью, и по уравнению определить, какая это будет линия.

Решение.

1). Составим таблицу

r

1,2

≈1,28

≈1,36

≈1,59

2

≈2,69

3

≈3,78

≈5,21

6

≈5,21

≈3,79

3

≈2,69

2

≈1,59

≈1,36

≈1,28

1,2



Из таблицы видно, что это эллипс. Для вычерчивания линии проведем радиус-векторы, соответствующие углам , взятым с интервалом ( /8 ). На каждом из этих радиус-векторах откладываем отрезки, равные значению r при соответствующим значении угла из таблице (112.1). Соединяя точки, являющие концами этих отрезков, получим график этой линии:

2). Подставляя и в уравнение заданной

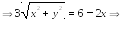
линии, получим:

Полученное уравнение есть уравнение эллипса с полуосями a = 11,25 и b = 4 с центром в точке А (2,4; 0) .

122. Найти указанные пределы, не пользуясь правилом Лопиталя.

а). б).

в). г).

Решение.

а). Подстановка предельного значения аргумента приводит к

неопределенности . Разделим числитель и знаменатель на старшую степень аргумента, т.е. на . Получим

, так как при

и - бесконечно малые функции.

б). Пределы числителя и знаменателя при равны 0, т.е. имеем

неопределенность . Избавимся от иррациональности в числителе,

помножим числитель и знаменатель на , получим

.

в). Заменяя и поделив числитель и знаменатель на , получим

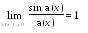
Здесь использован первый замечательный предел

г). Преобразуем , получим

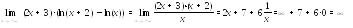
132. Заданы функция и два значения аргумента и .

Требуется:

1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента;

2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа;

3) сделать схематический чертеж.

Решение. Функция в точке непрерывна, так как в этой точке

непрерывна функция ,а также

Значение , есть точка разрыва второго рода, этой функции , так как

. Второй односторонний предел конечен:

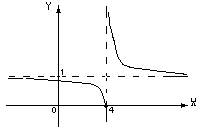
Чтобы сделать чертеж, найдем .

Изобразим схематично график функции

142. Задана функция различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

Решение. Функция х-3 непрерывна на , функция х+1 непрерывна на , а функция непрерывна на участке . Значит f(x) непрерывна на интервалах . Остается исследовать точки и . Находим правые и левые пределы функции в этих точках

То есть является точкой разрыва первого рода, так как

, но существуют. Для точки

Так как то в точке непрерывна.

Сделаем ее чертеж