курс 1, КОНТРОЛЬНАЯ 2, Вариант № 5

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛАРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного и дистанционного обучения

Специальность: Программное обеспечение информационных технологий

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ № 2

Вариант № 5

ФИО

Группа:

Зачетная книжка:

Электронный адрес:

Задача 45 Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

 

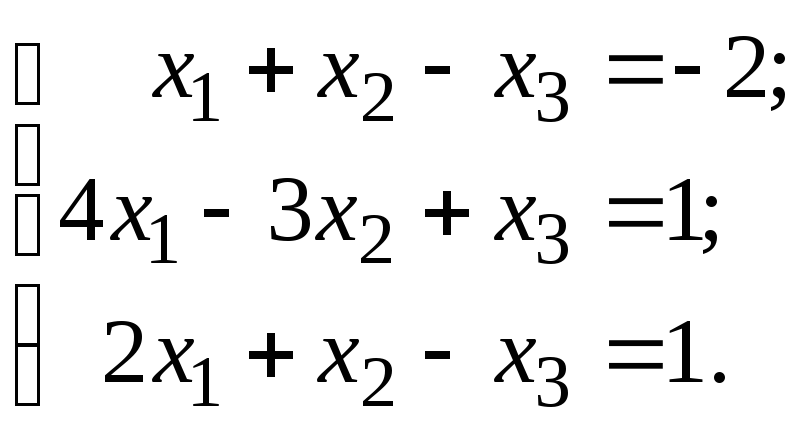
Составим матрицу коэффициентов (основную матрицу системы) и найдем её определитель:

.

Так как определитель отличен от нуля, то система совместна и имеет единственное решение.

1) по формулам Крамера:

;

;

.

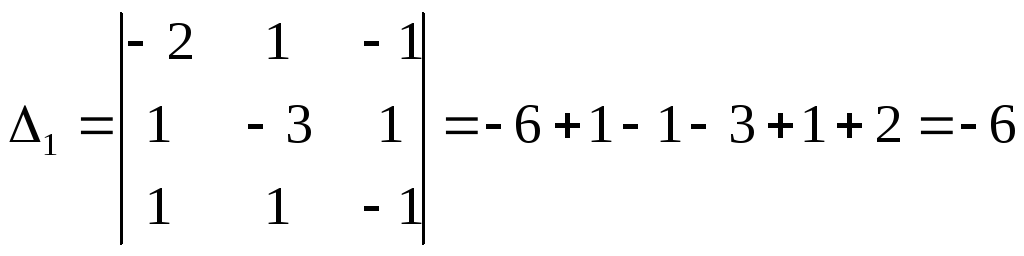Далее по формулам Крамера вычисляем:

Таким образом, система имеет единственное решение , , .

2) методом Гаусса:

Составим расширенную матрицу системы: .

Теперь приведём её путем элементарных преобразований к треугольному или трапециевидному виду.

Эквивалентна системе линейных уравнений:

Отсюда:

Ответ:, , .

3) матричный метод

Найдем обратную матрицу.

Определитель основной матрицы системы .

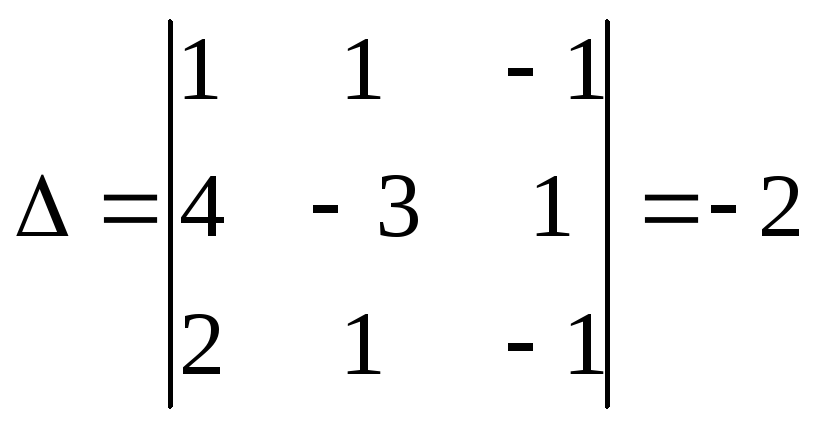Таким образом, обратная матрица к основной матрице системы имеет вид

.

Значит, матричное решение системы имеет вид: или

,

где , алгебраические дополнения элементов матрицы А

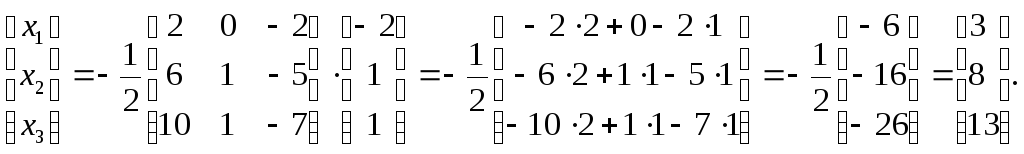
Отсюда следует, что , , .

Задача 55

Найти общее решение системы линейных уравнений.

Составим расширенную матрицу системы: .

Теперь приведём её путем элементарных преобразований к трапециевидной форме.

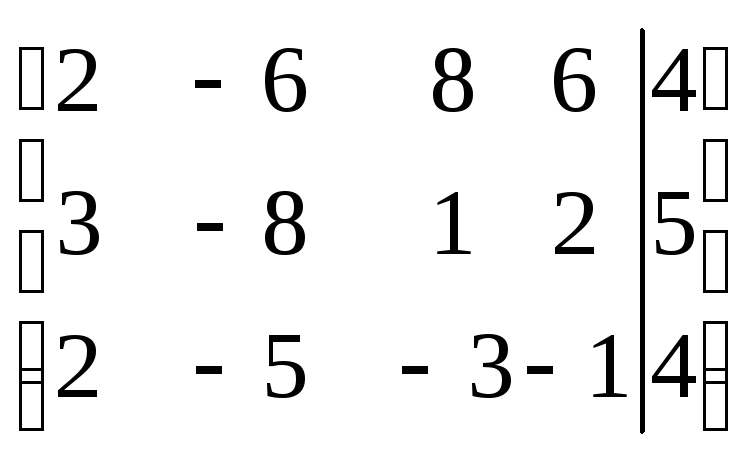
Так как , то система несовместна, решений нет.

Задача 65 Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

 

Составляем характеристическое уравнение матрицы А и находим его корни:

Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.

При система имеет вид:

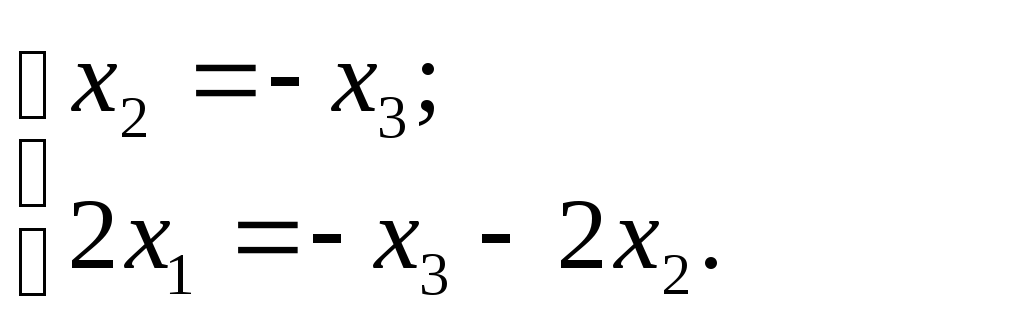
Значит, собственному значению соответствует собственный вектор

.

Здесь х₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным единице, получим собственный вектор в виде .

При система имеет вид:

Значит, собственному значению соответствует собственный вектор

.

Здесь х₂ – произвольное действительное число, не равное нулю. Соответствующий собственный вектор имеет вид .

При система имеет вид:

Собственному значению соответствует собственный вектор

.

Приняв , получим собственный вектор в виде .

Таким образом, матрица А имеет три собственных значения , , , а нормированные собственные векторы имеют вид

; ; .

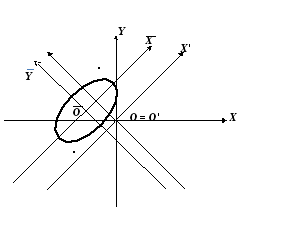
Задача 75 Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат.

.

Составим матрицу данной квадратичной формы и найдём её собственные значения:

.

Корнями характеристического уравнения являются числа и .

При :

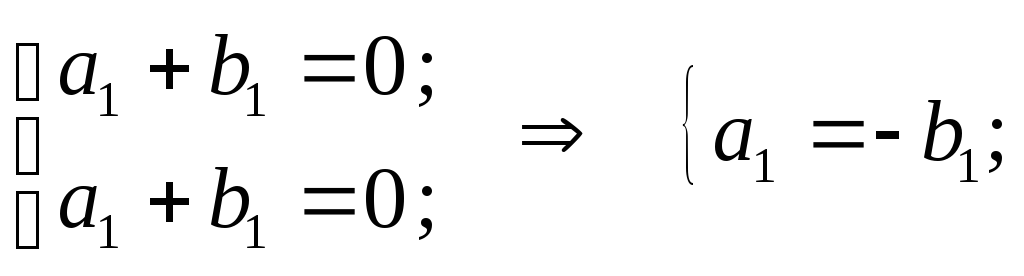собственный вектор .

При :

собственный вектор .

Нормируя собственные векторы, получим

и .

Матрица перехода Т к новому базису имеет вид

.

Вводим замену переменных

Подставим эти выражения в исходное уравнение кривой:

.

Введя замену , , получим уравнение эллипса: