Контрольная работа №4

ВАРИАНТ №3

Контрольная работа №4

Задание 1.

Найти производную данных функций.

а) б)

в) г)

д)

Решение:

а)

б)

в)

г)

Логарифмируя это равенство по основанию е, получаем

Дифференцируя получаем

д)

Задание 2.

Найти и

а)

б)

Решение:

а)

б)

Задание 3.

Применив формулу Тейлора с остаточным членом в форме Лагранжа к ф-ции f(x)=e^x ,вычислить с точностью до 0,001 значение e^a и e^b. Методом линейной интерпретации вычислить приближённое значение

a=0,19; b=0,22; x₀=0,16;

Решение:

Формула Тейлора с остаточным членом в форме Лагранжа для ф-ции

имеет вид

где

отсюда получаем

Значения и принадлежат отрезку и

При заданной погрешности и достаточном числе членов ряда Тейлора

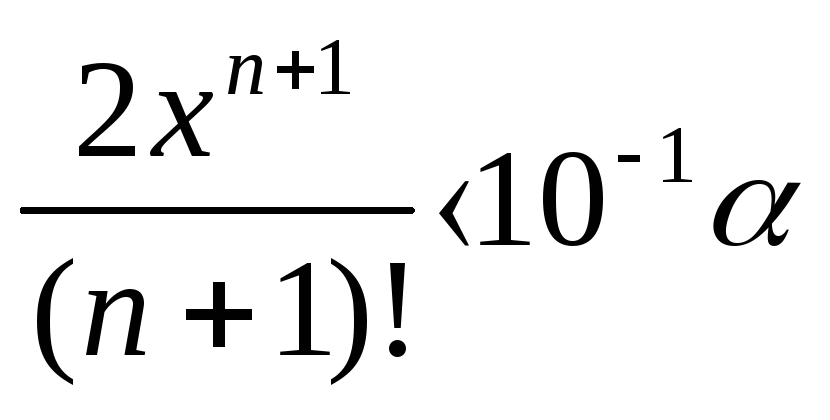откуда

при имеем

находим

при

точность достигается при

Запишем интерполяционный многочлен первой степени

Задание 4.

Найти наибольшее и наименьшее значение ф-ции на отрезках

,

Решение:

Критическая точка одна

эта точка принадлежит отрезку

Вычисляем значение ф-ции на концах отрезка и в критической точке

Ответ:

при ;

при ;

Задание 5.

В прямоугольной системе координат через точку (1, 2) проведена прямая с отрицательным угловым коэффициентом, которая вместе с осями координат образует треугольник. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей?

Задание 6.

Исследовать методами дифференциального исчисления функции и построить ее график, используя результаты исследования.

Задание 7.

Найти уравнение касательной и уравнение нормальной плоскости линии r = r(t) в точке t₀ .

221.