К.р. №1 4 вариант

Вариант 4

№4

Даны четыре вектора в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение:

Вычислим смешанное произведение векторов

Поскольку смешанное произведение этих векторов не равно нулю, то они не компланарны. Следовательно, они образуют базис.

Найдем координаты вектора в этом базисе:

№14

Даны координаты вершин пирамиды . Найти

1. Длину ребра ;

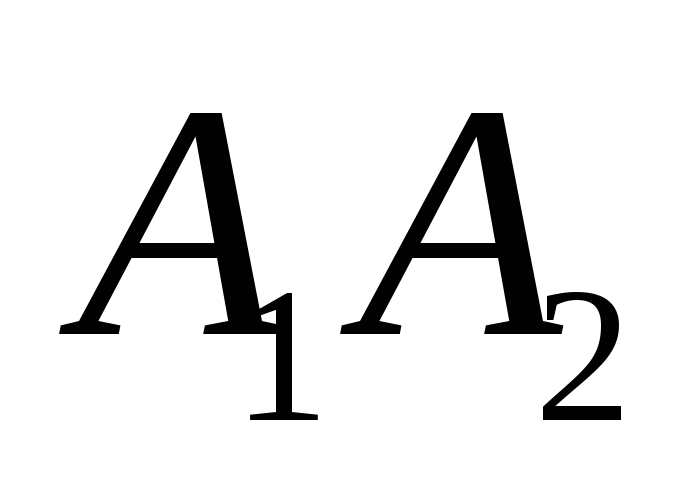2. Угол между ребрами и ;

3. Уравнение плоскости ;

4. Площадь грани ;

5. Объем пирамиды;

6. Уравнение прямой ;

7. Уравнение высоты, опущенной из вершины на плоскость .

8. Угол между ребром 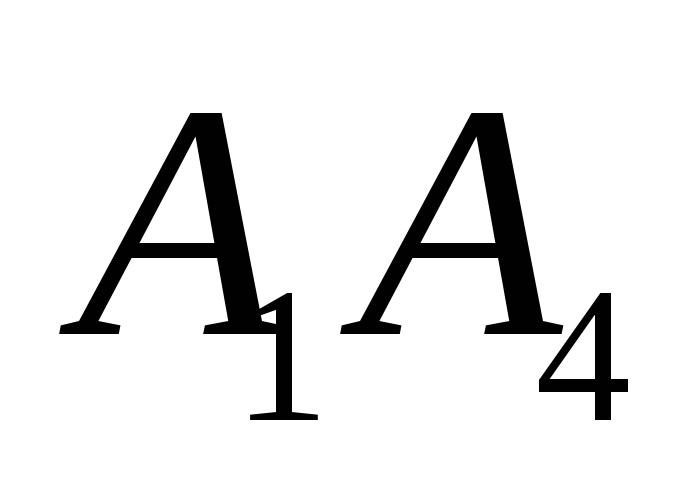и гранью ;

;;;.

Решение:

1. Найдем координаты вектора :

.

Длина ребра равна длине вектора :

.

2. Найдем координаты вектора :

.

Скалярное произведение векторов и равно:

.

Длина ребра равна длине вектора :

.

Тогда искомый угол равен:

3. Уравнение плоскости :

4. Найдем координаты вектора :

.

Площадь грани будет равно половине модуля векторного произведения векторов и :

5) Объем пирамиды будет равен одной шестой части модуля смешанного произведения векторов , и :

.

6) Уравнение прямой :

.

7) Направляющий вектор высоты, опущенной из вершины на плоскость , будет равен векторы нормали к плоскости :

.

Тогда уравнение этой высоты:

8) Угол между прямой и гранью :

№24

Составить уравнение линии, каждая точка которой находится вдвое ближе к точке , чем к точке .

Решение:

Ответ: .

№34

Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) методом Гаусса; 2) средствами матричного исчисления (с помощью обратной матрицы).

Решение:

Вычислим определить матрицы этой системы:

.

Поскольку количество неизвестных совпадает с количеством уравнений и определитель матрицы системы не равен нулю, то данная система является совместной.

1) Решим систему методом Гаусса

2)

Ответ: .

№44

Найти общее решение системы линейных уравнений.

Решение:

Определим ранг матрицы системы:

Ранг матрицы системы равен двум. Размерность пространства решений равна разности между числом неизвестных и рангом матрицы системы. Получаем 4-2=2.

Запишем систему в эквивалентном виде:

Для начала возьмем . Получаем:

Или.

Возьмем . Получаем:

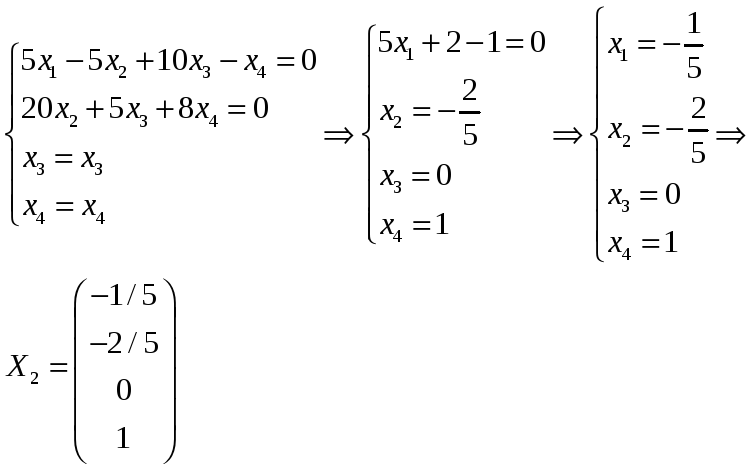
Или.

№54

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:

.

Решение:

Найдем собственные значения этой матрицы:

.

Найдем собственные векторы:

.

№64

Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат.

.

Решение:

Запишем матрицу квадратичной формы:

.

Найдем собственные значения этой матрицы:

.

Получаем:

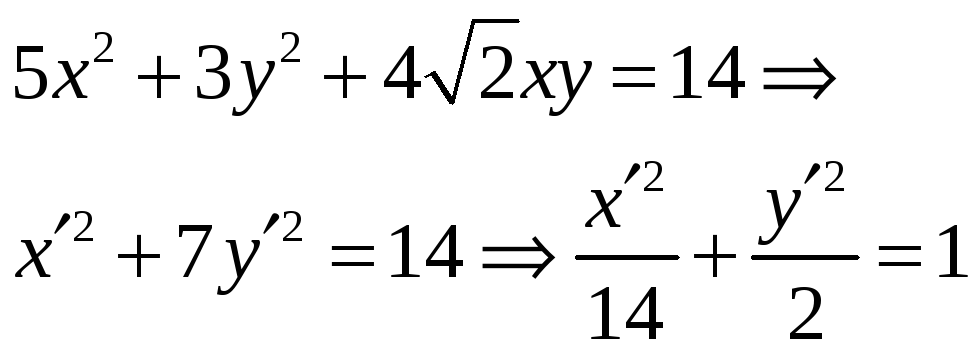- каноническое уравнение эллипса.

8