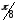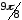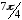Контрольная работа по ВМ №3

Контрольная работа №1

Выполнил: студент 1 курса, ПОИТ,

гр. 191002, Приходько Александр

Контрольная работа № 3. Введение в математический анализ

Задача 1(88)

Выделив в заданной функции полный квадрат, получить уравнение параболы и построить её график

Решение

Выделив полный квадрат в заданной функции, получим

.

Теперь применим метод преобразования координат. Известно, что график функции получают путем переноса графика вверх или вниз вдоль оси OY на в зависимости от знака b, график функции получается параллельным переносом графика при в положительном направлении оси ОХ на с, и в отрицательном направлении этой оси при. Тогда график исходной функции можно построить, переместив вершину параболы в точку . Ветви параболы направлены вниз.

Задача 2(98)

Задана функция на отрезке . Требуется: 1) построить график функции в полярной системе координат по точкам, давая аргументу значения через промежуток 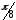; 2) найти каноническое уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить тип линии.

Решение

Составим таблицу значений:

	0
r	2	2,08	2,34	2,89	4	6,48	8	13,66	52,55

∞	52,55	13,66	8	6,48	4	2,89	2,34	2,08	2

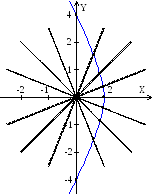
Для вычерчивания линии проведем радиусы-векторы, соответствующие углам , взятым с интервалом . На каждом из этих радиусов-векторов откладываем отрезки, равные значению r при соответствующем значении из таблицы . Соединяя точки, являющиеся концами этих отрезков, получаем график данной линии:

2. Подставляя и в уравнение заданной линии, получим

Полученное уравнение есть уравнение параболы

Задача 3

Найти указанные пределы, не пользуясь правилом Лопиталя.

1) 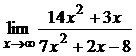; 2) ; 3) .

Решение

1) Подстановка предельного значения аргумента приводит к неопределённости вида . Разделим числитель и знаменатель на старшую степень аргумента, т.е. на . Получим

,

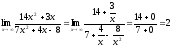так как при функции – бесконечно малые функции

2) Пределы числителя и знаменателя при 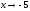равны нулю, т.е. имеем неопределенность . Домножим числитель и знаменатель на 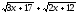_{, а многочлен в знаменателе разложим на множители}:

3) Подстановка 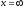приводит к неопределенности .

Воспользуемся свойством разности логарифмов и замечательным пределом

Задача 4

Найти указанные пределы, используя эквивалентные бесконечно малые функции.

1) ; 2) .

Решение

1)

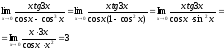
2) Введём замену переменной , тогда при .

Преобразуем выражение:

Здесь мы воспользовались соотношениями и эквивалентными функциями .

Задача 5(128)

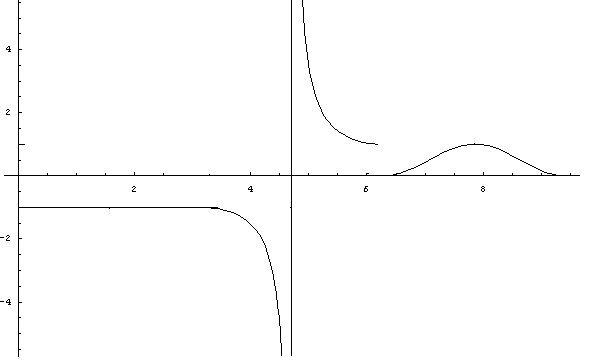
Задана функция различными аналитическими выражениями для различных интервалов изменения аргумента. Найти точки разрыва функции, если они существуют, и установить их тип. Сделать чертёж

Решение

Очевидно, что являются точками, подозрительными на разрыв. В остальных точках функция непрерывна.

Вычислим односторонние пределы в подозрительных точках:

; ;

; .

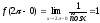Поскольку 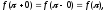то функция в точке является непрерывной.

В точке функция имеет разрыв 1‑го рода, так как .

Построим график с учетом проведенного исследования.