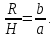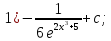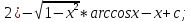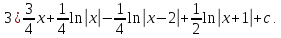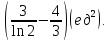КР №2 высшая математика 1 курс
.docxМинистерство образования республики Беларусь
Учреждение образования
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»
Институт информационных технологий
Специальность_________________________________
КОНТРОЛЬНАЯ РАБОТА №2
По курсу_____________________________________
Вариант №_____
Студент-заочник___ курса
Группы №______________
ФИО __________________
_______________________
Адрес__________________
_______________________
Тел. ___________________
Минск, 2009
Таблица ответов к задачам контрольной работы
|
Задача №1
1)
0; 2)
|
|
Задача №2
5) 12;
|
|
Задача №3
|
|
Задача №4
неравенство
|
|
Задача №5
Функция ни чётная, ни нечётная, ни переодическая;
Вертикальных
асимптот нет, наклонной асимптоты
справа нет,
|
|
Задача №6
|
|
Задача №7
|
|
Задача №8
|
|
Задача №9
|
|
Задача №10
|
Задача №1.
Вычислить пределы функций, не пользуясь правилом Лопиталя.
1)
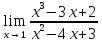 ; 2)
; 2)
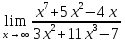 ;
3)
;
3)
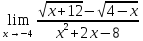 ;
;
4)
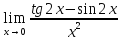 ; 5)
; 5)
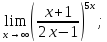 6)
6)
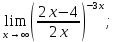
Решение:
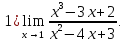
При x =
1 числитель и знаменатель дроби обращаются
в нуль, имеем неопределённость вида
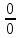 ,
чтобы раскрыть эту неопределённость
предварительно преобразуем дробь:
,
чтобы раскрыть эту неопределённость
предварительно преобразуем дробь:
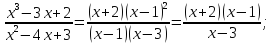
Переходим к пределу:
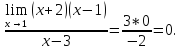
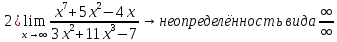
Разделим
числитель и знаменатель дроби на
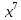 :
:
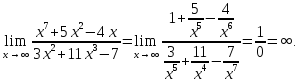
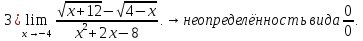
Домножим
числитель и знаменатель на выражение
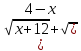 :
:
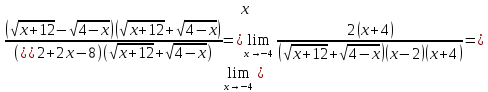
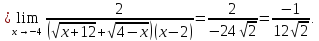
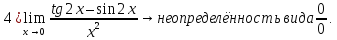
Упростим выражение, используя замену бесконечно малых функций соответствующими эквивалентами
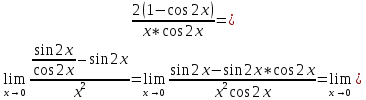
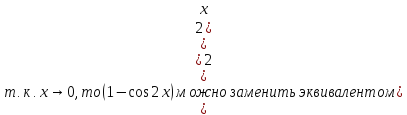
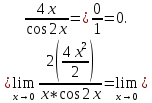
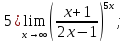
Можно
заметить, что основание степени стремится
к
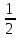 ,
так что получается формально
,
так что получается формально
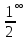 .
Это выражение не является неопределённостью
(в отличие от выражения
.
Это выражение не является неопределённостью
(в отличие от выражения 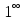 ),
так как основание степени при достаточно
больших
),
так как основание степени при достаточно
больших 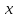 близко
к
близко
к
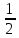 (и
заведомо меньше, скажем,
(и
заведомо меньше, скажем,
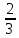 )
и при возведении в неограниченно
увеличивающуюся степень
)
и при возведении в неограниченно
увеличивающуюся степень 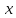 будет
меньше
будет
меньше
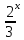 и,
следовательно, будет стремиться к 0.
и,
следовательно, будет стремиться к 0.
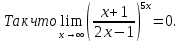
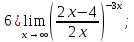
Приведём этот предел к виду 2го замечательного предела
(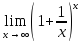 )
)
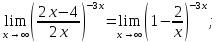
Произведём
замену:
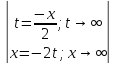 ;
;
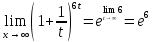 ;
;
Задача №2.
Вычислить:
1-3) производную
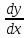 ;
4) производные
;
4) производные
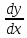 и
и
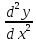 ;
5)
;
5)
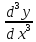 (
(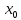 )
в данной точке
)
в данной точке
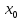 ;
6) производную n-го порядка данной функции
y(x).
;
6) производную n-го порядка данной функции
y(x).
1)
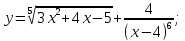 2)
2)
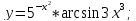
3)
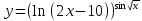 ;
4)
;
4)
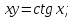
5)
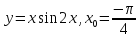 ;
6)
;
6)
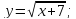
Решение:
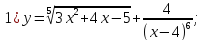
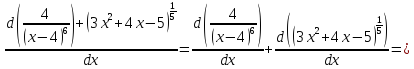
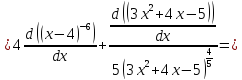
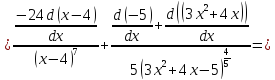
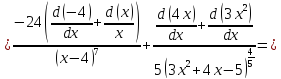
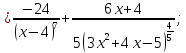
2)
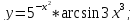
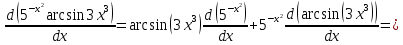
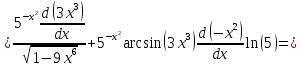
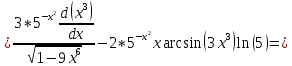
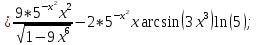
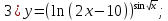
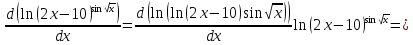
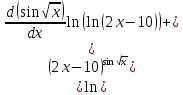
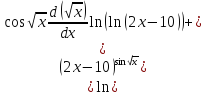
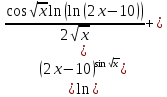
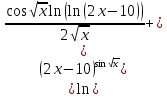
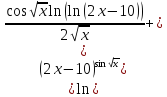
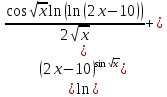
4)
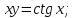
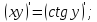
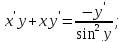
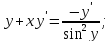
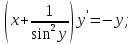
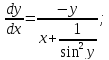


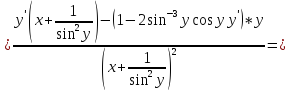
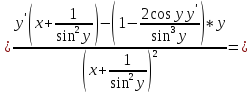
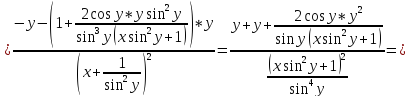
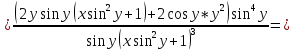
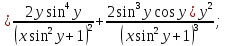
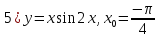
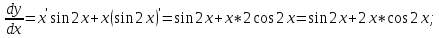
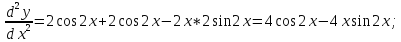
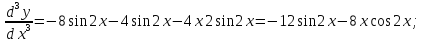
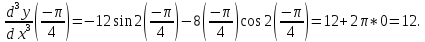
6)
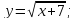
Сперва найдём производные: 1ю, 2ю, 3ю и 4ю данной функции.
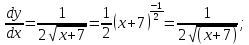
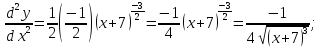

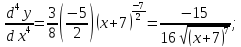
Исходя из полученых производных, составим формулу производной данной функции n-го порядка.
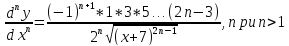
Задача №3.
Применяя
формулу Тейлора с остаточным членом в
формле Лагранжа вычислить значение
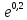 с точностью до 0,001.
с точностью до 0,001.
Решение:
Воспользуемся
формулой Тейлора с остаточным членом
в форме Лагранжа для функции
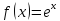 :
:
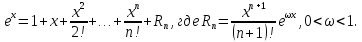
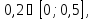 значит
значит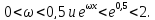
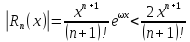
Будем производить вычисления с одним запасным знаком:
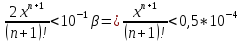
При
 имеем:
имеем:
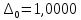 ;
;
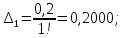
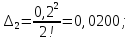
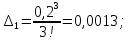
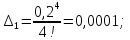
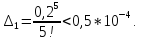

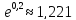
Задача №4.
Проверить
справедливость неравенства
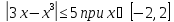 с
помощью исследования на экстремум.
с
помощью исследования на экстремум.
Решение:
Рассмотрим
функцию
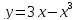 и найдём её наибольшее и наименьшее
значение на отрезке
и найдём её наибольшее и наименьшее
значение на отрезке
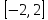 .
.
Найдём
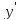 :
:

Найдём критические точки нашей функции:
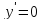
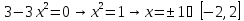
Вычислим значения функции в критических точках и на точках, являющихся концами отрезка:
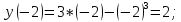
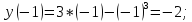
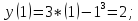
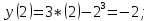
Значит,
max:
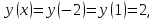
min:
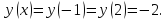
Исходя
из этого можно сделать вывод, что
неравенство
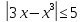 является справедливым.
является справедливым.
Задача №5.
Провести
полное исследование функции
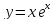 и построить её график.
и построить её график.
Решение:
Имеем
функцию
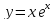 .
.
Произведём её поэтапное исследование с последующим построением графика.
1) Область определения:
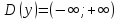
2)
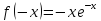 :
:
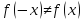 ,
,
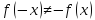 .
.
Функция ни чётная, ни нечётная, ни переодическая.
3) Точки пересечения с осями координат:
с
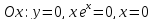 ;
;
с
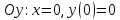 .
.
4) Промежутки монотонности и экстремумы функции:
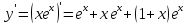
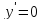 при
при
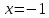
min
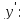
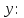

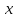
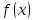 убывает
на промежутке
убывает
на промежутке
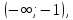
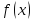 возрастает
на промежутке
возрастает
на промежутке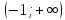 .
.
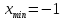
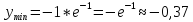
5) Промежутки выпуклости и вогнутости, точки перегиба:
Найдём их с помощью 2й производной.
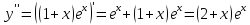
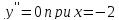
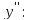
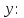
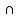
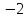
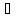
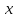
 выпукла
на промежутке
выпукла
на промежутке
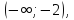
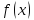 вогнута
на промежутке
вогнута
на промежутке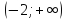 .
.
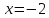 является
точкой перегиба.
является
точкой перегиба.
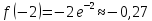 .
.
6) Асимптоты графика функции:
Наша
функция не имеет вертикальных асимптот,
поскольку отсутствуют точки разрыва
функции (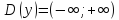 ).
).
Найдём
наклонную асимптоту
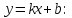
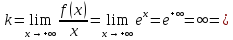
Наклонной асимптоты справа нет.
Наклоная асимптота слева:
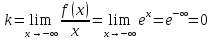
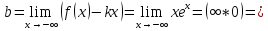
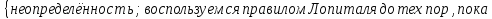
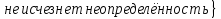
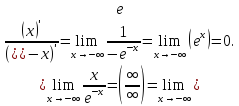
Прямая
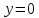 является горизонтальной асимптотой
слева.
является горизонтальной асимптотой
слева.
7) Построим
график функции
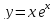 :
:
y

x
y = 0
-2
-1
0
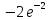
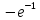



Задача №6.
Требуется изготовить открытый цилиндрический бак вместимостью V. стоимость одного квадратного метра материала из которого изготавливается дно бака, составляет a рублей, а стоимость одного квадратного метра материала, идущего на стенки бака, - b рублей. При каком отношении радиуса дна к высоте бака затраты на материалы будут минимальными?
Решение:
Пусть
R
– радиус основания бака,
H
R
Н – его высота. Площадь основания
находится
по формуле:
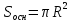

Площадь боковой поверхности
цилиндра находится по формуле:
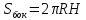
Стоимость материалов на изготов-
ление бака тогда составит:
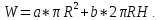
Так как объём цилиндра равен
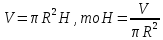
Получим
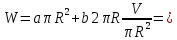
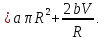
Произведём исследование функции W(R) на минимум:
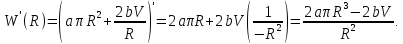
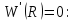
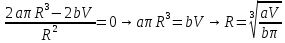
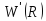 :
:
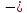
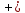
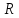
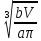
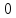
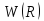 :
:
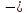
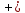
При
переходе через критческую точку
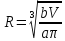 производная
производная
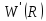
меняет
знак с «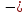 »
на «
»
на «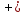 »,
следовательно, данная точка является
точкой минимума функции
»,
следовательно, данная точка является
точкой минимума функции
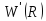 .
.
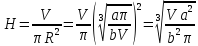
Отношение радиуса дна к высоте бака будет равно:
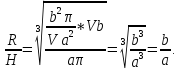
При данном отношении стоимость материалов, идущих на изготовления бака, будет минимальной.
Задача №7.
Найти неопределённые интегралы, в пунктах 1 и 2 результат проверить дифференыированием.
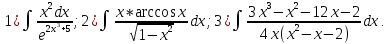
Решение:
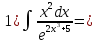
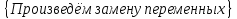
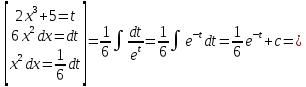
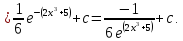
Проверка:
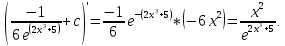
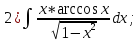
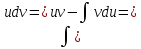
{Интегрируем по частям}
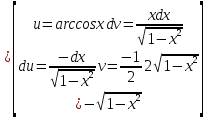
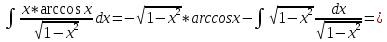
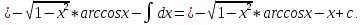
Проверка:
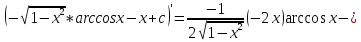
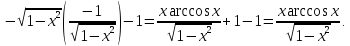
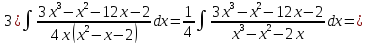
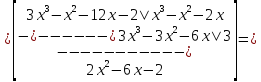
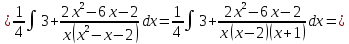
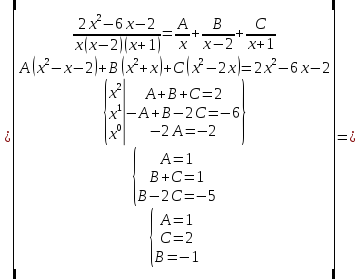
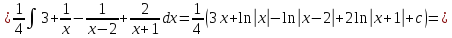
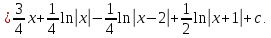
Задача №8.
Вычислить определённые интегралы:
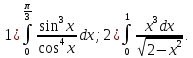
Решение:
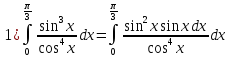
Сделаем подстановку:
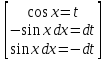
тогда
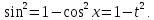
Изменим пределы интегрирования:
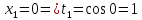
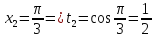
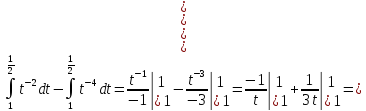
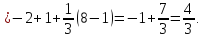
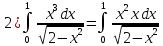
Сделаем подстановку:
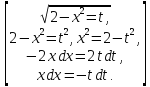
Изменим пределы интегрирования:
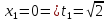
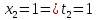
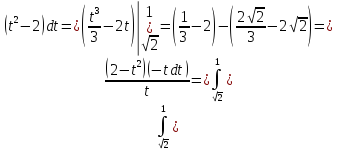
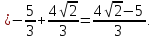
Задача №9.
Вычислить
приближённое значение
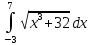
по методу:
1) прямоугольников;
2) Симпсона, разбивая промежуток интегрирования на 10 частей.
Все вычисления производить с точностью до трёх десятичных знаков после запятой.
Решение:
1)
Рассмотрим функцию
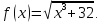 Вычислим приближённое значение
определённого интеграла по методу
прямоугольников:
Вычислим приближённое значение
определённого интеграла по методу
прямоугольников:
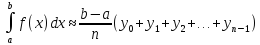
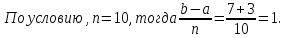
Вычислим
значения функции
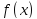 при
при
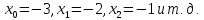
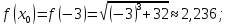
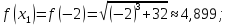
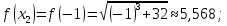
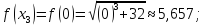
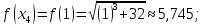
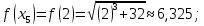
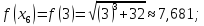
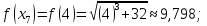
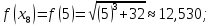
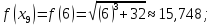
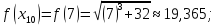
Таким образом,

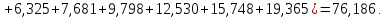
2) Вычислим приближённое значение определённого интеграла по формуле Симпсона:
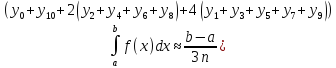
Поскольку
в предыдущем варианте расчёта мы уже
получили все значения
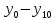 ,
то сейчас просто подставим их в наше
уравнение.
,
то сейчас просто подставим их в наше
уравнение.
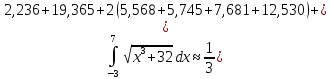
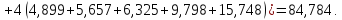
Задача №10.
Вычислить площадь фигуры, ограниченной линиями:
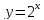 ,
,
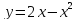 ,
, 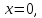
 .
.
Решение:
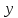
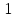
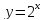
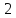
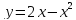
Вычислим площадь фигуры с помощью определённого интеграла по формуле:
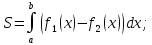
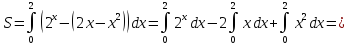

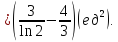

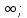 3)
3)
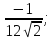 4) 0; 5) 0; 6)
4) 0; 5) 0; 6)
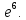
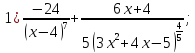
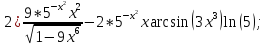
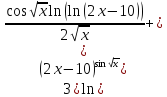
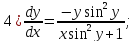
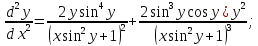
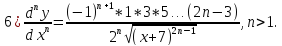
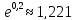
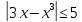 является справедливым.
является справедливым.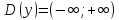 ;
;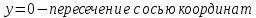 ;
;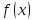 убывает
при
убывает
при
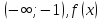 возрастает при
возрастает при
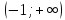 ;
;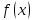 выпукла
при
выпукла
при
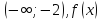 вогнута при
вогнута при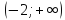 ;
;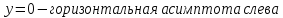 .
.