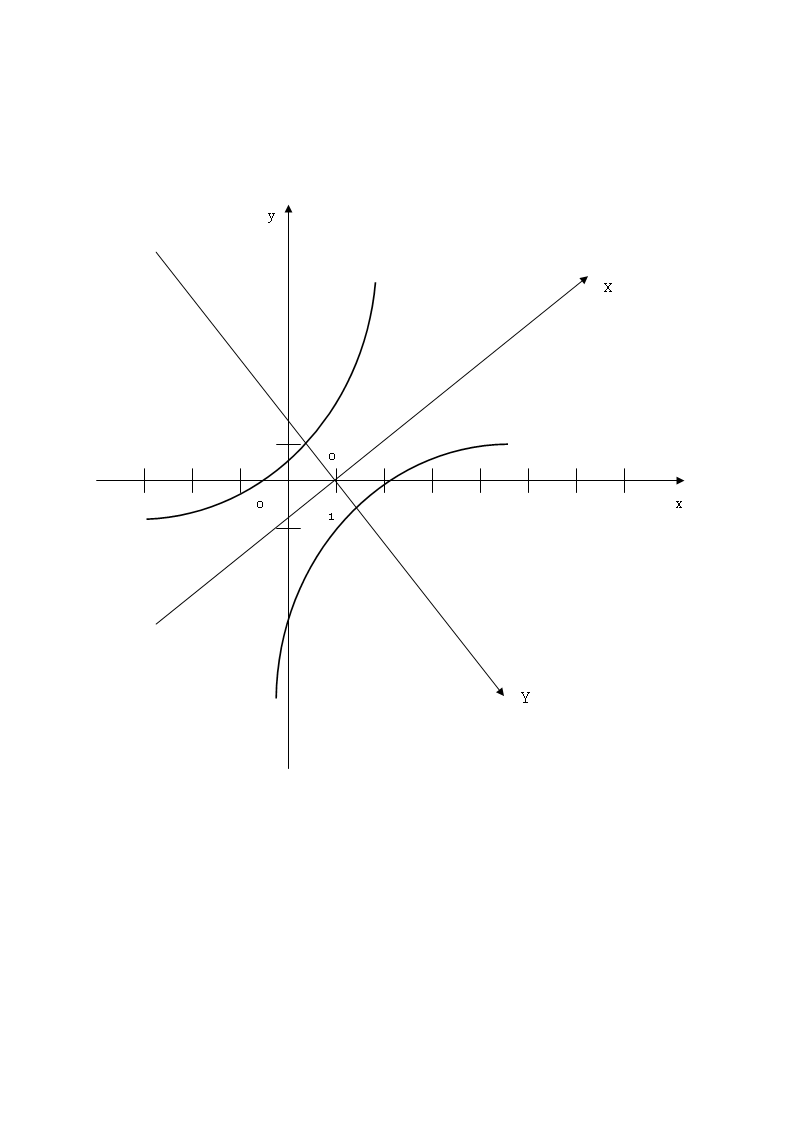контрольная №2

Контрольная работа №2

Элементы линейной алгебры

Задачи 41-50. Даны две матрицы A и B. Требуется найти: 1); 2) A^-1; 3) , где E - единичная матрица третьего порядка.

41. , .

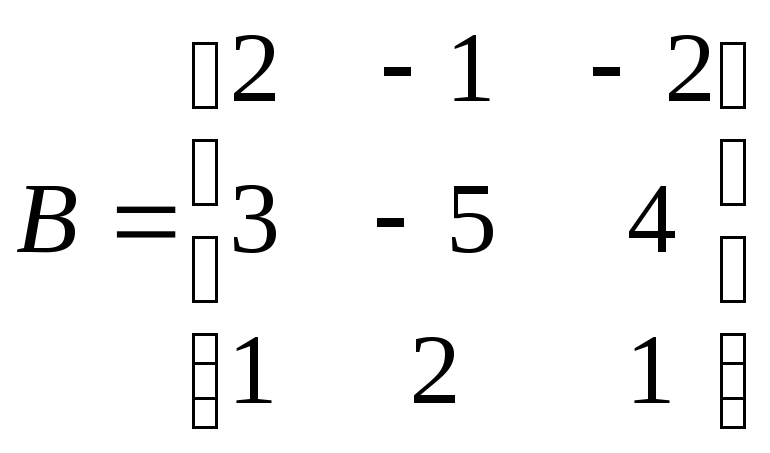1)

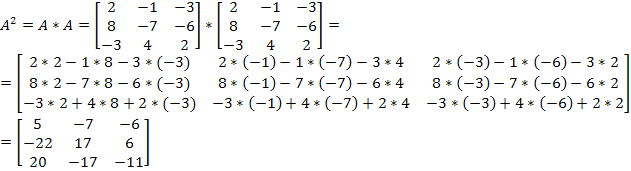
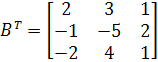
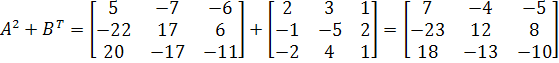
Ответ;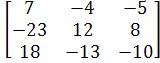

2) A^-1 – матрица, обратная матрице А

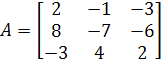
Вычислим определитель матрицы А

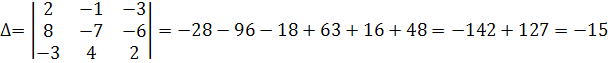
Вычислим алгебраические дополнения элементов матрицы:

Матрица, присоединенная к матрице А имеет вид:

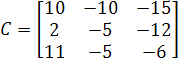
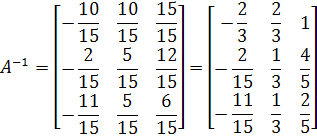
Ответ:

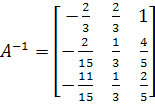
3) , где E - единичная матрица третьего порядка.

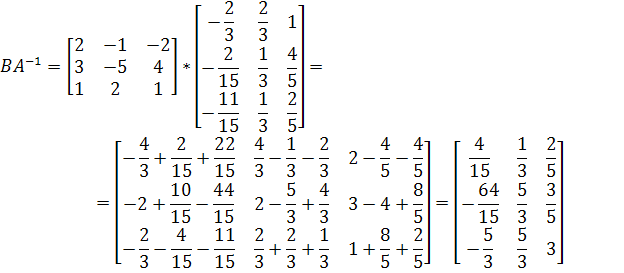
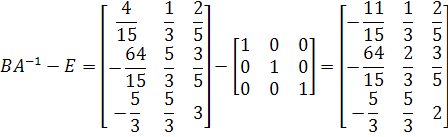
Ответ:

Задачи 51-60. Проверить, совместна ли система уравнений, и в случае совместности решить ее: 1) по формулам Крамера; 2) методом Гаусса; 3) с помощью обратной матрицы (матричным методом).

51.

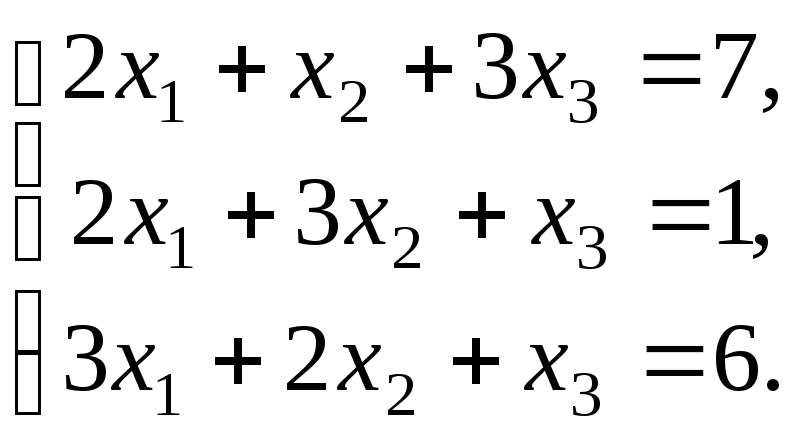
Матрица А системы имеет вид:

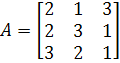
Вычислим определитель матрицы А:

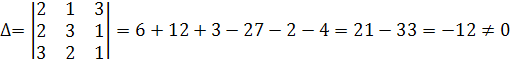
Следовательно, система совместна.

1)решим систему по формуле Крамера:

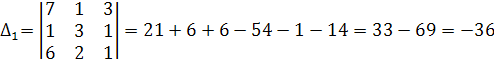
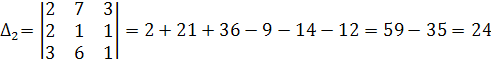
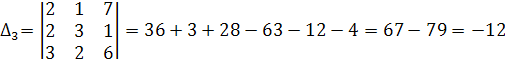
Ответ:

2)решим систему методом Гаусса:

Составим матрицу из коэффициентов при неизвестных и свободных членов, преобразуем ее:

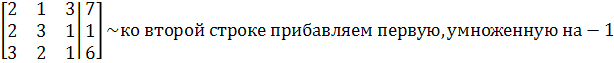
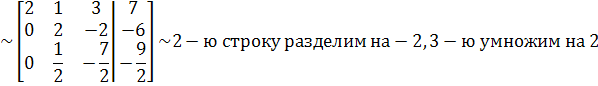
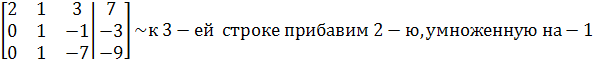
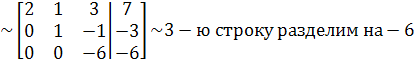
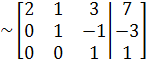
Система принимает вид: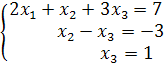

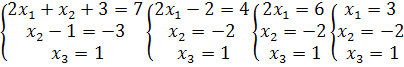
Ответ:

3)решим систему уравнений матричным методом.

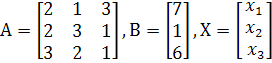
Найдем . Для этого вычислим определитель системы

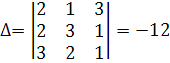
Вычислим алгебраические дополнения элементов матрицы:

Матрица, присоединенная к матрице А, имеет вид.

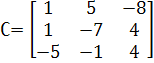
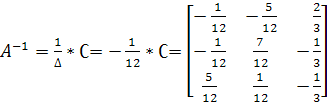
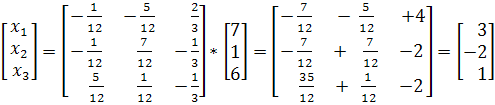
Ответ:

Задачи 61-70. Найти собственные значения и собственные векторы матрицы A.

61.

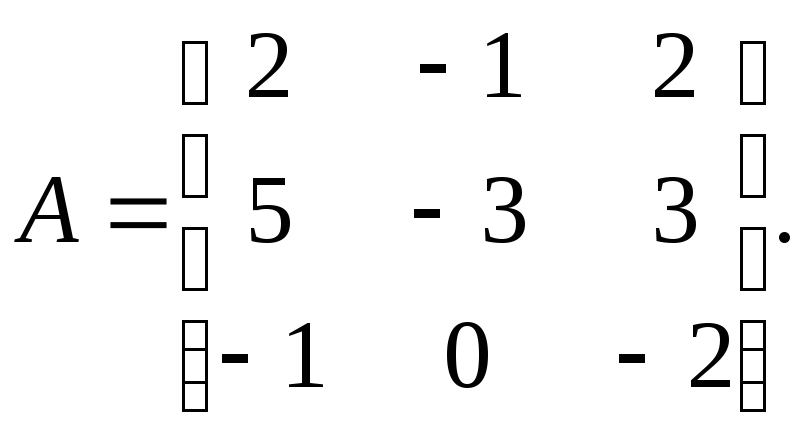
Для нахождения собственных значений матрицы А составим характеристическое уравнение:

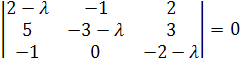
Для нахождения собственного вектора, соответствующего найденному собственному значению, составим и решим систему уравнений.

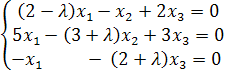
Подставим в нее , получим:

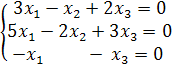
Решим методом Гаусса:

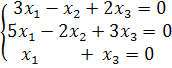
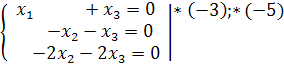
Одно из решений имеет вид:

Таким образом, собственные векторы матрицы А имеют вид:

Ответ: ;

Задачи 71-80. Используя теорию квадратичных форм, привести уравнение кривой второго порядка к каноническому виду и построить эту кривую.

71.

Рассмотрим квадратичную форму

Ее матрица имеет вид:

Приведем данную квадратичную форму к каноническому виду

Характеристическое уравнение матрицы А имеет вид:

Найдем собственные векторы, соответствующие полученным собственным значениям. Координаты (s,t) этих векторов определяются из системы уравнения.

При имеем: При имеем:

Положив , получим:

) - собственные векторы

Пронормировав эти векторы, запишем их координаты в столбцы и составим матрицу В

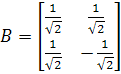
Искомое ортогональное преобразование имеет вид:

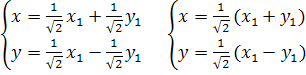
Подставим эти выражения в формулу данного уравнения:

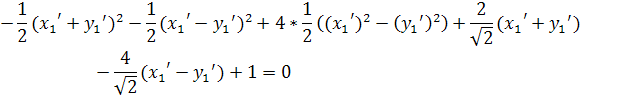
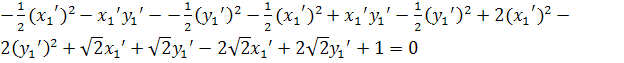
Выделим в левой части уравнения полные квадраты:

Новые координаты:

Получим уравнение вида:, которое определяется гиперболу с действительной осью О₁Y.

Найдем координаты нового начала координат О₁

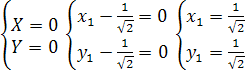
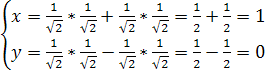O₁(1;0)

Решим систему относительно x₁ и y₁:

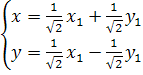
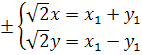
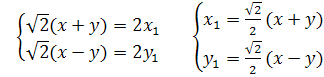
В новой системе координат XOY уравнения осей гиперболы имеют вид Y=0, X=0, поэтому имеем:

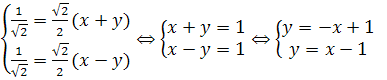- уравнение осей гиперболы в старой системе координат.