КР №2 по вышке 2 вариант

Агаджанов Владимир Леонидович

Факультет: З и Д О

Курс:1

Вариант:2

Контрольная работа по высшей математике

Контрольная работа №2

Тема 2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

5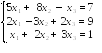2. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

.

Решение.

1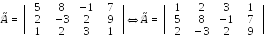. При решении системы методом Гаусса действия производятся над расширенной матрицей

с целью приведения ее путем элементарных преобразований к треугольному или трапециевидному виду. Для этого прибавим ко 2-й строке 1-ю,

у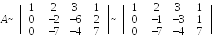множенную на ( - 5), к 3-й строке прибавим 1-ю, умноженную на (- 2), получим

п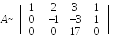рибавим к 3-й строке 2-ю, умноженную на ( -7), получим

Таким образом, ранги основной и расширенной матриц равны 3. Система имеет единственное решение. Она сводится к системе

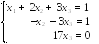
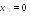
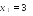
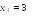
О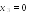тсюда, подставляя во второе уравнение, получим ,а из первого уравнения .Итак, , , .

2. Для решения этой задачи матричным способом, находим определитель системы

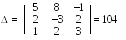
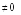
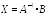
С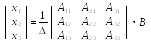ледовательно, находим решение по формуле или

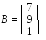
, где , 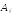- алгебраические

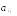
дополнения элементов матрицы А :

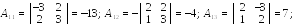
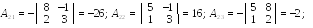
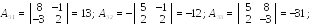
Проверим правильность вычисления обратной матрицы

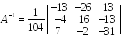
исходя из определения обратной

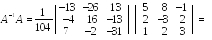
матрицы

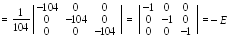
Значит, матричное решение системы имеет вид:

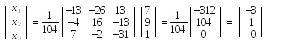
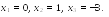
Откуда следует, что

62. Найти размерность и базис пространства решений однородной системы линейных уравнений.

Решение. Так как система уравнений состоит из трех уравнений с четырьмя неизвестными то дополним его уравнением вида ,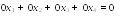

Следовательно система примет вид:

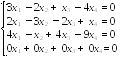
Находим ранг основной матрицы системы с помощью элементарных преобразований:

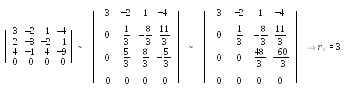
Т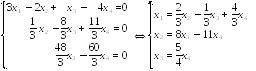ак как ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы

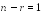. Преобразованная система, эквивалентная исходной, имеет вид

Эти формулы дают общее решение. В векторном виде его можно записать следующим образом

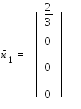
г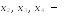де произвольные числа. Векторы-столбцы ,

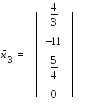
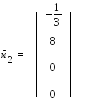
и образуют базис пространства решений

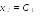
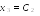
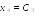
данной системы. Полагая , и ,где

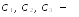
п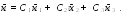роизвольные постоянные, получим общее решение в векторном виде:

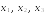
7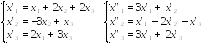2. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее через .

Р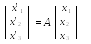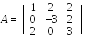ешение. Первое линейное преобразование

имеет матрицу ,

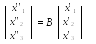
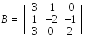
второе имеет матрицу .

Тогда произведение линейных преобразований имеет матрицу 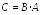, т.е.

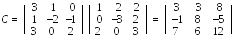
поэтому искомое линейное преобразование имеет вид

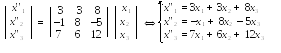
8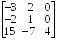2. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

А =

Решение. С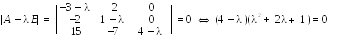оставляем характеристическое уравнение матрицы

,

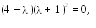
что соответствует откуда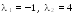

При система примет вид:

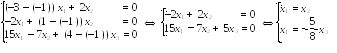
Т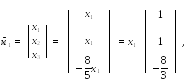аким образом, числу соответствует собственный вектор

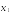
г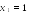де - произвольное действительное число. В частности, при

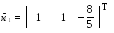
и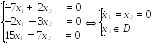меем .

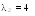
Аналогично для имеем , здесь

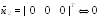
D – множество действительных чисел. Следовательно .

92 . Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.

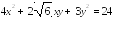
Решение. Левая часть уравнения представляет собой квадратичную форму с

матрицей . Решаем характеристическое уравнение

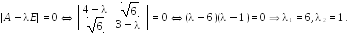
Найдем собственные векторы, имея две системы:

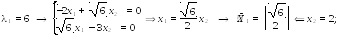
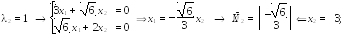
Нормировав эти векторы, запишем их координаты в столбцы, составив матрицу :

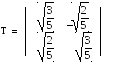
С помощью матрицы T записываем искомое ортогональное преобразование

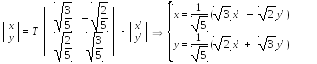
Э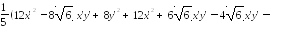то преобразование приводит данную квадратичную форму к каноническому виду

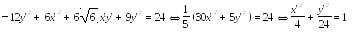
Последнее уравнение есть каноническое уравнение эллипса.