Задача №6.

Найти собственные значения и собственные векторы матрицы.

A =

Решение:

Составляем характеристическое уравнение матрицы А:

=0

Решим это уравнение путём разложения по 1й строке:

.

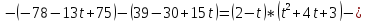
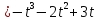или

методом подбора находим корни этого уравнения:

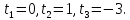–эти корни являются собственными значениями матрицы А.

Для отыскания соответствующих собственных векторов матрицы А используем системы уравнений и решим их:

При :

Решим данную систему методом Гаусса: Сформируем расширенную матрицу :

2 3 -3      0 13 3 2 -5      0 5 3 -6      0

Разделим строку 1 на a1,1 =

2

Получим матрицу :

1 3 2 -3 2      0 13 3 2 -5      0 5 3 -6      0

Вычтем из строки 2 строку 1 умноженную на a2,1=

Вычитаемая строка :

13 3 13 2 -13 2      0

Модифицированная матрица :

1 3 2 -3 2      0 0 -9 2 3 2      0 5 3 -6      0

Вычтем из строки 3 строку 1 умноженную на a3,1=

5

Вычитаемая строка :

5 15 2 -15 2      0

Модифицированная матрица :

1 3 2 -3 2      0 0 -9 2 3 2      0 0 -9 2 3 2      0

Разделим строку 2 на a2,2 =

-9 2

Получим матрицу :

1 3 2 -3 2      0 0 1 -1 3      0 0 -9 2 3 2      0

Вычтем из строки 3 строку 2 умноженную на a3,2=

-9 2

Вычитаемая строка :

0 -9 2 3 2      0

Модифицированная матрица :

1 3 2 -3 2      0 0 1 -1 3      0 0 0 0      0

3-ю строку из матрицы удалим (она обнулилась). Редуцированная матрица :

1 3 2 -3 2      0 0 1 -1 3      0

Вычтем из строки 1 строку 2 умноженную на a1,2=

3 2

Вычитаемая строка :

0 3 2 -1 2      0

Модифицированная матрица :

1 0 -1      0 0 1 -1 3      0

Выпишем систему уравнений по последней расширенной матрице:

		x1				-		x3	=		0
					x2	-	1 3	x3	=		0

x₁, x₂ оствавим в левой части уравнений, а x₃ перенесем вправо. Окончательный вид системы следующий:

x1

=

x3

x2

=

1 3

x3

x₃ - свободная переменная.

Полагая, что x3 = 1, получим: x1 = 1; x2 = .

Собственный вектор b₁ = (1, , 1)

При :

Решим данную систему методом Гаусса:

Сформируем расширенную матрицу :

1 3 -3      0 13 3 1 -5      0 5 3 -7      0

Вычтем из строки 2 строку 1 умноженную на a2,1=

Вычитаемая строка :

13 3 13 -13      0

Модифицированная матрица :

1 3 -3      0 0 -12 8      0 5 3 -7      0

Вычтем из строки 3 строку 1 умноженную на a3,1=

5

Вычитаемая строка :

5 15 -15      0

Модифицированная матрица :

1 3 -3      0 0 -12 8      0 0 -12 8      0

Разделим строку 2 на a2,2 =

-12

Получим матрицу :

1 3 -3      0 0 1 -2 3      0 0 -12 8      0

Вычтем из строки 3 строку 2 умноженную на a3,2=

-12

Вычитаемая строка :

0 -12 8      0

Модифицированная матрица :

1 3 -3      0 0 1 -2 3      0 0 0 0      0

3-ю строку из матрицы удалим (она обнулилась). Редуцированная матрица :

1 3 -3      0 0 1 -2 3      0

Вычтем из строки 1 строку 2 умноженную на a1,2=

3

Вычитаемая строка :

0 3 -2      0

Модифицированная матрица :

1 0 -1      0 0 1 -2 3      0

Выпишем систему уравнений по последней расширенной матрице:

x1

x3

=

0

x2

2 3

x3

=

0

x₁, x₂ оствавим в левой части уравнений, а x₃ перенесем вправо. Окончательный вид системы следующий:

x1

=

x3

x2

=

2 3

x3

x₃ - свободная переменная. 

Полагая, что x₃ = 1, получим:

x1 = 1;

x2 = ;

x3 = 1.

Собственный вектор b₂ = (1, , 1)

При :

Решим данную систему методом Гаусса: Сформируем расширенную матрицу :

5 3 -3      0 13 3 5 -5      0 5 3 -3      0

Разделим строку 1 на a1,1 =

5

Получим матрицу :

1 3 5 -3 5      0 13 3 5 -5      0 5 3 -3      0

Вычтем из строки 2 строку 1 умноженную на a2,1=

13 3

Вычитаемая строка :

13 3 13 5 -13 5      0

Модифицированная матрица :

1 3 5 -3 5      0 0 12 5 -12 5      0 5 3 -3      0

Вычтем из строки 3 строку 1 умноженную на a3,1=

5

Вычитаемая строка :

5 3 -3      0

Модифицированная матрица :

1 3 5 -3 5      0 0 12 5 -12 5      0 0 0 0      0

3-ю строку из матрицы удалим (она обнулилась). Редуцированная матрица :

1 3 5 -3 5      0 0 12 5 -12 5      0

Разделим строку 2 на a2,2 =

12 5

Получим матрицу :

1 3 5 -3 5      0 0 1 -1      0

Вычтем из строки 1 строку 2 умноженную на a1,2=

3 5

Вычитаемая строка :

0 3 5 -3 5      0

Модифицированная матрица :

1 0 0      0 0 1 -1      0

Выпишем систему уравнений по последней расширенной матрице:

x1

=

0

x2

-

x3

=

0

x₁, x₂ оствавим в левой части уравнений, а x₃ перенесем вправо. Окончательный вид системы следующий:

x1

=

0

x2

=

x3

x₃ - свободная переменная. 

Полагая, что x₃ = 1, получим:

x1 = 0

x2 = 1

x3 = 1

Собственный вектор b₃ = (0, 1, 1).
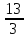