Министерство образования республики Беларусь

Учреждение образования

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»

Институт информационных технологий

Специальность_________________________________

Контрольная работа №1

По курсу_____________________________________

Вариант №_____

Студент-заочник___ курса

Группы №______________

ФИО __________________

_______________________

Адрес__________________

_______________________

Тел. ___________________

Минск, 2009

Таблица ответов к задачам контрольной работы

Задача №1: 1) ; 2) ; 3) не коллинеарны, ортогональны; 4) образуют базис; 5) d = ;		Задача №2: 1) ; 2) , 3) ; 4) N( 2.25,0.15); 5) ; 6) ;
Задача №3: 1) 2) 3) 4) 5)
Задача №4: A-1BT = ATB-1 =
Задача №5: , , .	Задача №6: –собственные значения. Собственные векторы матрицы: b1 = (1, , 1)b2 = (1, , 1)b3 = (0, 1, 1)
Задача №7: d = 1; .	Задача №8: Кривая – парабола. рисунок - см. страницу 46 контрольной работы.

Задача №1.

Даны векторы a, b, c, d. Треубется:

1. вычислисть скалярное произведение векторов a и b;

2. найти модуль векторного произведения векторов b и c;

3. проверить коллинеарность и ортогональность векторов c и d;

4. проверить, образуют ли векторы a, b, c базис;

5. если да, найти координаты вектора d в этом базисе.

Значения радикалов и отношений вычислить с точностью до второго знака.

a = ,

b = ,

c = ,

d = .

Решение:

1) Скалярное произведение двух векторов a = (X₁, Y₁, Z₁), b = (X₂, Y₂, Z₂) выражается формулой: ab = X₁ X₂ + Y₁ Y₂ + Z₁ Z₂, т.е. скалярное произведение двух векторов равно сумме произведений одноименных координат.

ab = 4*6 – 14*6 – 12*7 = .

2) Модуль векторного произведения [b,c] равен площали параллелограмма, построенного на этих векторах и вычисляется по формуле:

.

==

.

3) Равенство [c,d] = 0 выражает необходимое и достаточное условие коллинеарности векторов c и d.

Вычислим векторное произведение векторов c и d для определения коллинеарности:

[c,d] =

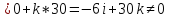
векторы не коллинеарны.

Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е. эти векторы перпендикулярны друг другу, а это возможно тогда и только тогда, когда их скалярное произведение равно нулю.

Вычислим скалярное произведение векторов c и d для определения ортогональности:

cd = векторы ортогональны.

4) Согласно свойству смешанного произведения трёх векторов, векторы a, b, c образуют базис, если они линейно не зависимы, т.е. их смешанное произведение не равно нулю.

Смешанное произведение 3х векторов находится по формуле:

abc = .

Найдём смешанное произведение векторов a, b, c:

abc =

векторы не компланарны и образуют базис.

5) Согласно теореме о линейной зависимости векторов, вектор d можно разложить по трём не компланарным векторам a, b, c единственным образом:

.

Это равенство равносильно системе следующих уравенений:

Решим данную систему уравнений по формуле Крамера:

Система линейных уравнений:

Определители:

, ,,

.

Решение:

, ,.

Составим определители матриц для нашей системы линейных уравнений:

, ,,

.

Решим эти определители:

;

;

;

.

Найдём x, y, z:

Подставив полученные значения x, y, z в начальное равенство для вектора d, получим:

d = .