Контрольная работа3

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра программного обеспечения информационных технологий

Факультет ФНиДО

Специальность ПОИТ

Контрольная работа № 3

по дисциплине «ВЫСШАЯ МАТЕМАТИКА»

часть 1

Вариант № 6

Выполнил студент: Бондаренко С.В.

группа 191001

Зачетная книжка № 191001-6

Минск 2011

Введение в математический анализ

86. Выделив в заданной функции полный квадрат, получить уравнение параболы и построить её график.

Решение: Для выделения полного квадрата проведем следующие действия

.

В результате получили уравнение параболы с вершиной в точке (1; 5) и ветвями, направленными вниз. График параболы представлен ниже

96. Дана функция 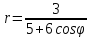на отрезке 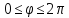. Требуется: 1) построить график функции в полярной системе координат по точкам, давая φ значения через промежуток , начиная от φ = 0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Решение: Определим значения функции с шагом :

φ = 0, r(φ) = 0,273; φ = , r(φ) = 0,285; φ = , r(φ) = 0,325;

φ = , r(φ) = 0,411; φ = , r(φ) = 0,6; φ = , r(φ) = 1,11;

φ = , r(φ) = 3,961; φ = , r(φ) = -5,522; φ = , r(φ) = -3;

φ = , r(φ) = -5,522; φ = , r(φ) = 3,961; φ = , r(φ) = 1,11;

φ = , r(φ) = 0,6; φ = , r(φ) = 0,411; φ = , r(φ) = 0,325;

φ = 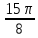, r(φ) = 0,285; φ = , r(φ) = 0,273.

По полученным значениям строим график, представленный ниже

Для перехода к прямоугольной системе координат воспользуемся формулами:

Выражая rи cos(φ) через х и у, получаем

Подставляя в начальное выражение, получаем:

В результате преобразований имеем:

Получили каноническое уравнение гиперболы.

106. Найти указанные пределы не пользуясь правилом Лопиталя:

а)

б)

в)

Сделаем замену переменной , принимая во внимание, что. Тогда

116.Найти указанные пределы, используя эквивалентные бесконечно малые функции.

а)

Произведем замену на бесконечно малые функции: при

В результате получаем

б)

Введём замену переменной , тогда при.

Преобразуем выражение:

126. Задана функция различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

Решение: Для определения точек разрыва найдем односторонние пределы в точках х₁ = 0, х₂ = 2.

Односторонние пределы в точке 0 равны, следовательноразрыва в данной точке нет. В точке 2 односторонние пределы не равны, но оба предела конечны.Следовательно, имеет место точка устранимого разрыва первого рода. Также в точке 3 функция не определена. Найдем односторонние пределы в этой точке

Можно сделать вывод, что в точке 3 существует разрыв второго рода.

График функции представлен ниже