К.р. №2. 9 вариант
.docxЗадача 79.
Построить
график функции
 преобразованием графика функции
преобразованием графика функции
 :
:
 .
.
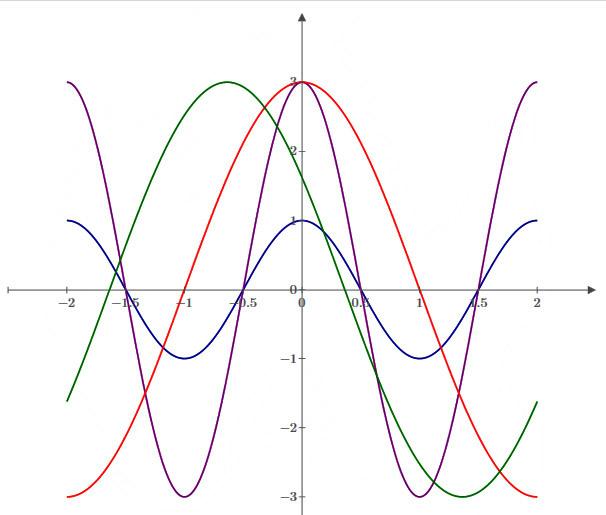
Шаг 1. Построим график функции y=cos x
Шаг 2. Построим график функции y=3cos x. Он будет представлять собой график функции у=cos x вытянутой в три раза в высоту.
Шаг
3. Построим график функции
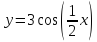 Он
будет представлять собой
график функции y=3cos
x,
растянутой в 2 раза по горизонтали.
Он
будет представлять собой
график функции y=3cos
x,
растянутой в 2 раза по горизонтали.
Шаг
4. Построим график функции
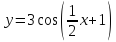 .
Он будет представлять собой график
функции
.
Он будет представлять собой график
функции
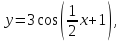
 .
.
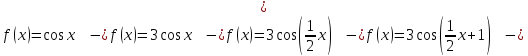
Задача 89.
Дана
функция
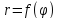 на отрезке
на отрезке
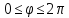 .
требуется: 1) построить график функции
в полярной системе координат по точкам,
давая
.
требуется: 1) построить график функции
в полярной системе координат по точкам,
давая
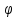 значения через промежуток
значения через промежуток
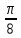 ,
начиная от
,
начиная от
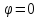 ;
2) найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось абсцисс
– с полярной осью, и по уравнению
определить, какая это будет линия.
;
2) найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось абсцисс
– с полярной осью, и по уравнению
определить, какая это будет линия.
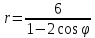 .
.
1) Для построения графика создадим таблицу соответствия радиусов углам
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
78,82 |
20,49 |
9,72 |
6,00 |
4,34 |
3,51 |
3,12 |
3,00 |
3,12 |
3,51 |
4,34 |
6,00 |
9,72 |
20,49 |
78,82 |
График имеет следующий вид:
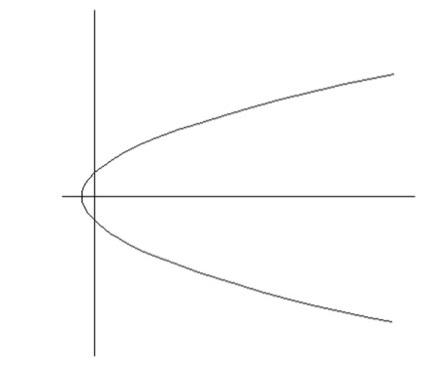
2) Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат.
Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами (x, y) и полярными координатами (r, ) существует следующая связь:
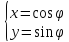 ;
;
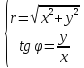 ;
откуда
;
откуда
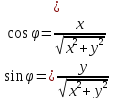
Поставив
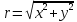 и
и
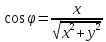 в исходное уравнение получим
в исходное уравнение получим
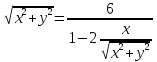
После преобразований получим искомое уравнение:
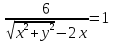
Ответ:

Задача 99.
Найти указанные пределы не пользуясь правилом Лопиталя:
а)
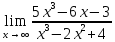 ; б)
; б)
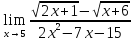 ;
;
в)
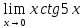 ; г)
; г)
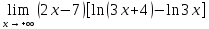 .
.
а)
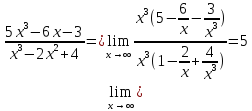
б)
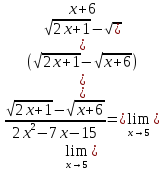
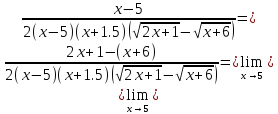
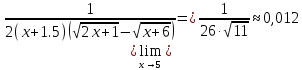
в)
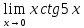
Используем
бесконечно малые значения функции
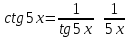
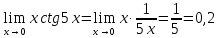
г)
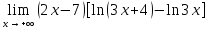
Используем свойства алгоритмов для преобразования
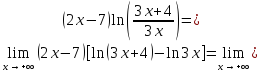
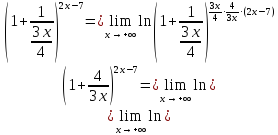
Применив следствие из второго замечательного предела получим
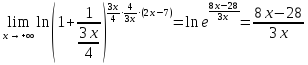
Ответ:
а) 5; б)
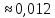 ;
в) 0,2; г)
;
в) 0,2; г)
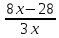 .
.
Задача 109.
Заданы
функция
 и два значения аргумента x1
и x2.
Требуется: 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы при приближении к точке разрыва
слева и справа; 3) сделать схематический
чертеж.
и два значения аргумента x1
и x2.
Требуется: 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы при приближении к точке разрыва
слева и справа; 3) сделать схематический
чертеж.
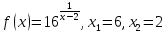 .
.
1)
Для точки
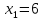
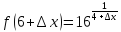
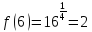
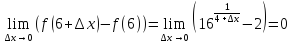
следовательно функция непрерывна
Для
точки
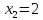
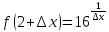
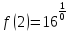 следовательно
следовательно
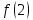 не
определена.
не
определена.
2)
В точке
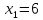
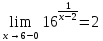 ;
;
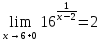
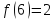 непрерывна
в точке
непрерывна
в точке
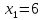
В
точке
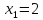
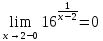 ;
;
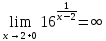
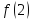 не
определена, разрыв второго рода.
не
определена, разрыв второго рода.
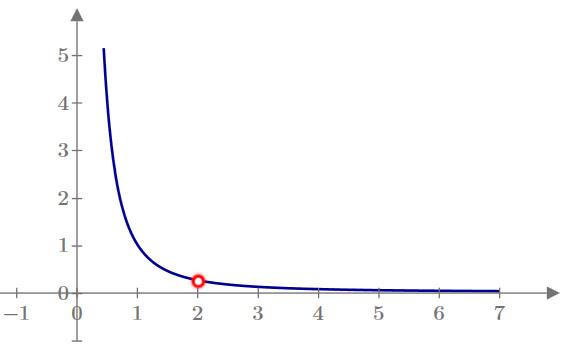
3) схематический чертеж:
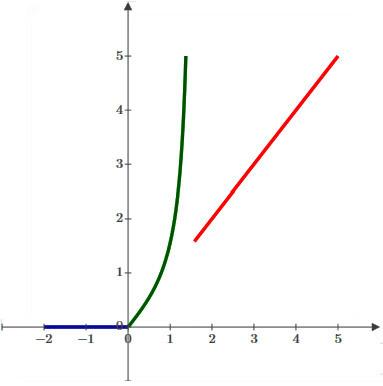
Задача 119.
Задана функция y=f(x) различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

Функция
f(x)
определена и непрерывна на интервалах
 ,
где она задана непрерывными функциями,
следовательно, разрыв возможен только
в точках
,
где она задана непрерывными функциями,
следовательно, разрыв возможен только
в точках
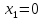 и
и
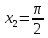
Для
точки
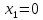
Значение
функции в точке
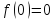 ;
;
Предел
функции слева
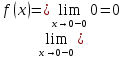 ;
;
Предел
функции справа
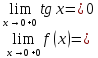 .
.
Оба
предела существуют и равны значению
функции в точке, следовательно, функция
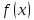 в
точке
в
точке
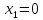 непрерывна.
непрерывна.
Для
точки
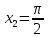
Значение
функции в точке
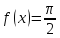 ;
;
Предел
функции слева
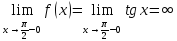 ;
;
Предел
функции справа
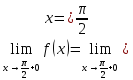 .
.
Функция
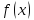 определена в точке
определена в точке
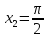 ,
имеет оба предела, но т.к. предел слева
равен бесконечности, имеет разрыв
второго рода в данной точке.
,
имеет оба предела, но т.к. предел слева
равен бесконечности, имеет разрыв
второго рода в данной точке.