Контрольная работа № 1

по дисциплине

«Высшая математика»

вариант 9

Задание 9

Даны четыре вектора (1,0,5), (3,2,7), (5,0,9) и (-4,2,-12) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.

Решение

Базисом в пространстве R³ являются любые три некомпланарных вектора. Условием компланарности трех векторов является равенство их смешанного произведения нулю. Итак, находим:

Так как смешанное произведение векторов не равно нулю, то векторы некомпланарны и образуют базис.

Для вычисления координат вектора в этом базисе составим систему уравнений в координатном виде:

Решим ее по формулам Крамера. Определитель Δ = –32.

Найдем определители .

Имеем ; ; .

Значит, .

Ответ:

Задание 19

Даны координаты вершин пирамиды A₁A₂A₃A₄: А₁(7,5,3), А₂(9,4,4), А₃(4,5,7), А₄(7,9,6). Найти: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃; 4) площадь грани А₁А₂А₃; 5) объём пирамиды; 6) уравнения прямой А₁А₂; 7) уравнение плоскости А₁А₂А₃; 8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертёж.

Решение

1. Находим координаты вектора = (9 – 7, 4 – 5, 4 – 3) = (2,–1, 1) и длину ребра = = ≈ 2,45.

2. Угол  между ребрами и вычисляется по формуле

из скалярного произведения.

,

= (7 – 7, 9 – 5, 6 – 3) = (0; 4; 3);

= .

.

Поэтому ; φ =

3. Угол  между ребром и плоскостью - это угол между вектором и его ортогональной проекцией на грань .

Вектор перпендикулярен грани , что вытекает из определения векторного произведения векторов и :

= (4 – 7; 5 – 5; 7 – 3) = (–3; 0; 4).

Синус искомого угла θ равен косинусу между векторами , .

≈–0,8773.

θ = arcsin≈ –1,07 рад ≈ –61°19′.

4. Площадь грани равна половине модуля векторного произведения векторов и , на которых построена грань.

.

5. Объем пирамиды численно равен одной шестой модуля смешанного произведения векторов , , :

= · |–12 – 32 – 9| = .

6. Для составления уравнений прямой воспользуемся формулой:

,

где – координаты точки , - координаты точки .

;

.

В таком виде уравнения прямой называются каноническими. Они могут быть записаны и в виде

или ,

т.е. уравнение прямой как линии пересечения двух плоскостей.

7. Для составления уравнения плоскости воспользуемся формулой

,

где - координаты , - координаты , - координаты .

;;

(x – 7) · – (y – 5) · + (z – 3) · =

= –4 · (x – 7) – 11 · (y – 5) – 3 · (z – 3) = 0,

–4 · (x – 7) – 11 · (y – 5) – 3 · (z – 3) =

= –4x + 28 – 11y + 55 – 3z + 9 =

= –4x –11y – 3z + 92 = 0 – уравнение плоскости А₁А₂А₃.

8. Искомые уравнения высоты получим из канонических уравнений прямой , где - точка, лежащая на искомой прямой; - координаты вектора , параллельного искомой прямой. При этом в качестве точки возьмем точку , а в качестве вектора возьмем нормальный вектор плоскости , т.е. . Имеем:

.

9. Сделаем чертеж

Задание 29

Составить уравнение линии, каждая точка которой отстоит от точки A(4,0) вдвое дальше, чем от прямой х = 1.

Решение

Обозначим произвольную точку искомой линии M(x, y). Тогда по условию , где Р – основание перпендикуляра из точки M к прямой х = 1.

|AM| = = ;

|PM| = |x – 1|.

Значит, = 2 · |x – 1|.

Возведем обе части равенства в квадрат:

х² – 8x + 16 + у² = 2x – 2;

х² – 10x + у² + 14 = 0;

(х² – 10x + 25) – 25 + у² + 14 = 0;

(х – 5)² + у² – 11 = 0;

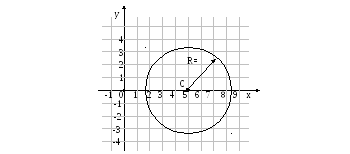
(х – 5)² + у² = 11.

Это каноническое уравнение окружности с радиусом R = ≈ 3,3 и центром в точке С(5; 0).

Сделаем чертеж:

Задание 39

Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления:

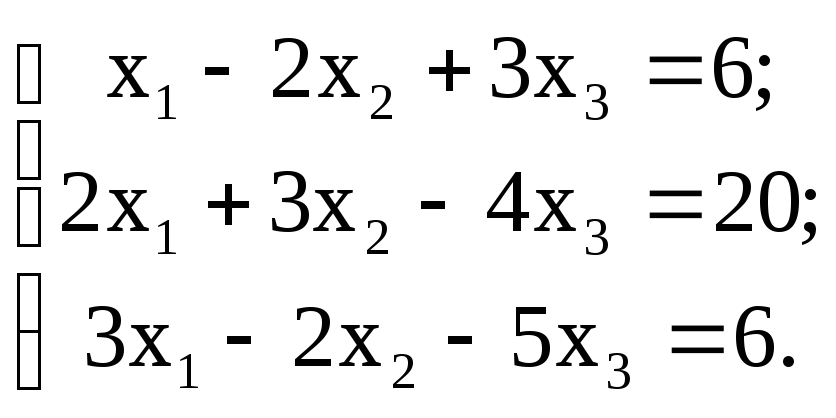
Решение

Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований найдем ранг матрицы

А =

данной системы и ранг расширенной матрицы

.

Прибавим ко второй строке первую, умноженную на (–2), к третьей строке прибавим первую, умноженную на (–3), получим:

.

К третьей строке прибавим вторую, умноженную на –, получим:

.

Таким образом, ранги основной и расширенной матриц равны 3, т.е. числу неизвестных. Значит, исходная система совместна и имеет единственное решение.

1) Решим систему методом Гаусса. Последней матрице соответствует система:

Прямой ход метода Гаусса завершен. Обратным ходом находим:

х₃ = = 2; х₂ = (8 + 10 · 2) / 7 = 4; х₁ = 6 + 2 · 4 – 3 · 2 = 8.

х₁ = 8; х₂ = 4; х₃ = 2 – решение системы.

2) Решим систему матричным методом. Находим определитель Δ основной матрицы системы:

Δ = = –15 + 24 – 12 – 8 – 20 – 27 = –58;

Так как Δ = –58 0, то значит, находим решение по формуле

или = , где 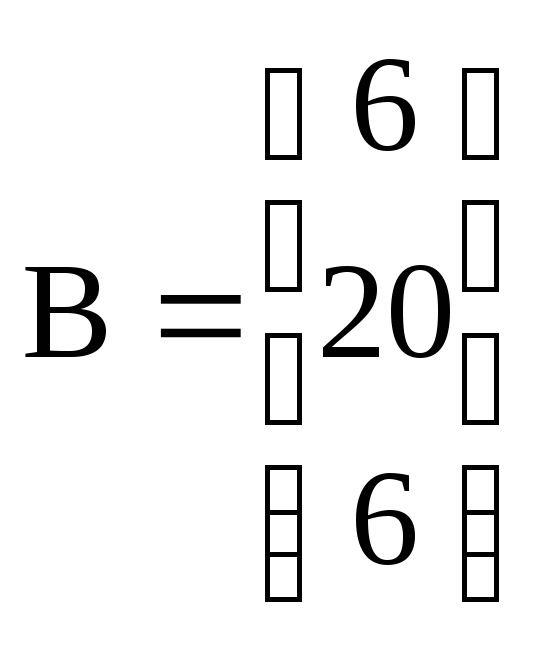, – алгебраические дополнения элементов матрицы А:

А₁₁ = (–1)¹⁺¹ · = –15 – 8 = –23;

А₁₂ = (–1)¹⁺² · = –(–10 + 12) = –2;

А₁₃ = (–1)¹⁺³ · = –4 – 9 = –13;

А₂₁ = (–1)²⁺¹ · = –(10 + 6) = –16;

А₂₂ = (–1)²⁺² · = –5 – 9 = –14;

А₂₃ = (–1)²⁺³ · = –(–2 + 6) = –4;

А₃₁ = (–1)³⁺¹ · = 8 – 9 = –1;

А₃₂ = (–1)³⁺² · = –(–4 – 6) = 10;

А₃₃ = (–1)³⁺³ · = 3 + 4 = 7.

Составим обратную матрицу:

.

Находим матричное решение системы:

Х = .

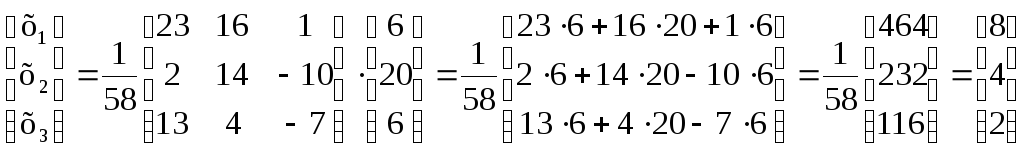Отсюда следует, что х₁ = 8; х₂ = 4; х₃ = 2.

Ответ: х₁ = 8; х₂ = 4; х₃ = 2.

Задание 49

Найти размерность и базис пространства решений однородной системы линейных уравнений

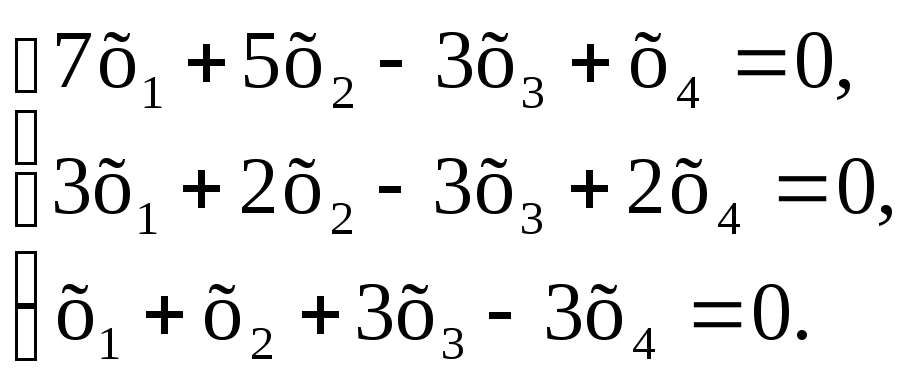
Решение

С помощью элементарных преобразований найдем ранг основной матрицы системы:

.

Поменяем местами первую и третью строки, затем умножим первую строку на (–3) и сложим со второй, умножим первую строку на (–7) и сложим с третьей, получим:

.

Ранг системы равен r = 2, а число неизвестных n = 4. Так как ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы n – r = 4 – 2 = 2. Преобразованная система, эквивалентная исходной, имеет вид:

х₁ + х₂ +3х₃ – 3х₄ = 0, х₁ + х₂ = –3х₃ + 3х₄,

–х₂ –12 х₃ +11х₄ = 0, х₂ = –12х₃ + 11х₄,

х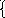₁ = –3х₃ +3х₄ +12х₃ – 11х₄, х₁ = 9х₃ – 8х₄,

х₂ = –12х₃ + 11х₄, х₂ = –12х₃ + 11х₄.

Эти формулы дают общее решение. В векторном виде его можно записать следующим образом:

,

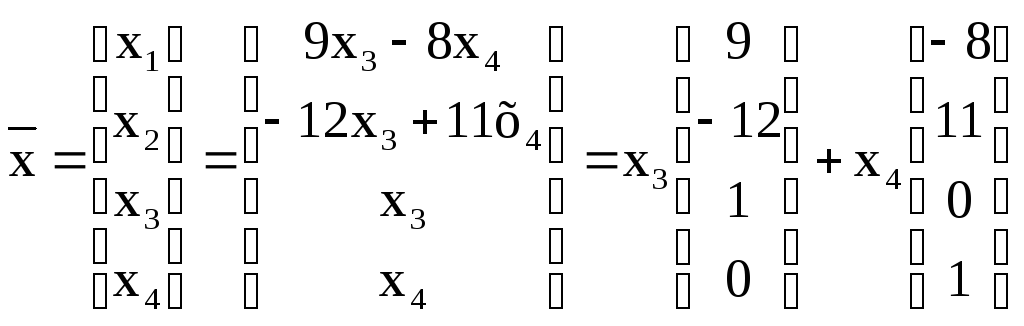где и – произвольные числа. Вектор-столбцы и образуют базис пространства решений данной системы.

Полагая х₃ = с₁, х₄ = с₂, где с₁, с₂ – произвольные постоянные, получим общее решение в векторном виде .

Задание 59

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

.

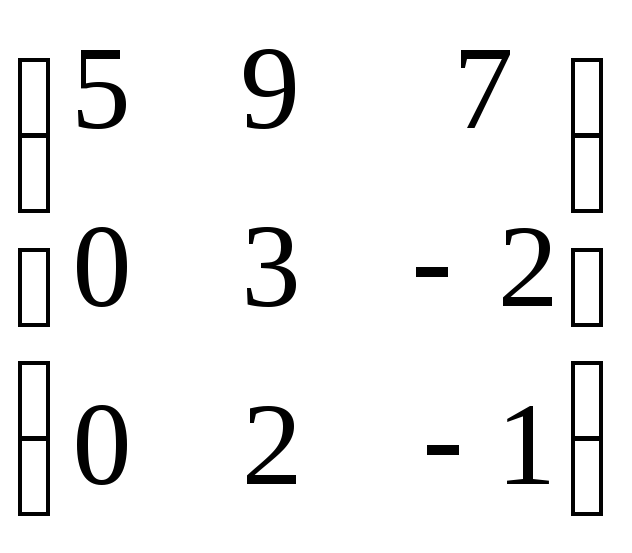Решение

Составляем характеристическое уравнение матрицы

;

(5 – λ) (3 – λ) (–1 – λ) +4 (5 – λ) = 0;

(5 – λ) (–3 – 3λ + λ+ λ² +4) = 0;

(5 – λ) (λ² – 2λ + 1) = 0;

5 – λ = 0 или λ² – 2λ + 1 = 0;

λ₁ = 5; D = 4 – 4 = 0;

λ_2,3 = 1.

λ₁ = 5, λ_2,3 = 1 – собственные значения линейного преобразования.

Для отыскания собственных векторов используем систему уравнений:

(5 – λ)х₁ +9х₂ + 7х₃ = 0,

(3 – λ)х₂ –2 х₃ = 0,

2х₂ + (–1 – λ)х₃ = 0,

При λ₁ = 5 получим систему:

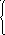
9 х₂ + 7х₃ = 0, х₁ – любое х₁ – любое,

–2х₂ –2 х₃ = 0, –6х₃ –2 х₃ = 0 х₃ = 0,

2х₂ – 6х₃ = 0. х₂ = 3 х₃ х₂ =0.

Таким образом, числу λ₁ = 1 соответствует собственный вектор

,

где х₁ – произвольное действительное число.

В частности, при х₁ = 1 имеем .

При λ_2,3 = 1 получим систему:

4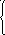х₁ +9 х₂ + 7х₃ = 0, 4х₁ = 16х₃, х₁ = 4х₃,

2х₂ – 2х₃ = 0, х₂ = х₃, х₂ = х₃,

2х₂ –2 х₃ = 0, х₃ – любое. х₃ – любое.

Числу λ_2,3 = 1 соответствует собственный вектор

,

где х₃ – произвольное действительное число.

В частности, при х₃ = 1 имеем .

Итак, матрица А имеет три собственных значения λ₁ = 5, λ₂ = 1 (кратности 2).

Соответствующие им собственные векторы (с точностью до постоянного множителя) равны и .

Задание 69

Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.

6х² + 2ху +3у² = 16.

Решение

Левая часть уравнения 6х² + 2ху + 3у² = 16 представляет собой квадратичную форму с матрицей .

Решаем характеристическое уравнение

т.е. .

(6 – λ)(3 – λ) – 10 = 0;

18 – 9λ + λ² – 10 = 0;

λ² – 9λ + 8 = 0;

D = 81 – 32 = 49;

λ₁ = (9 – 7) / 2 = 1, λ₂ = (9 + 7) / 2 = 8.

λ₁ = 1, λ₂ = 8 – характеристические числа.

Находим собственные векторы из системы уравнений .

Полагая λ = λ₁ = 1, получаем систему уравнений для первого вектора :

х₂ = –х₁ = – х₁ .

Пусть х₁ = , тогда х₂ = – и – собственный вектор, соответствующий λ₁=1.

Полагая λ = λ₂ = 8, получаем систему уравнений для второго вектора :

х₁ = х₂ =х₂.

Пусть х₂ = , тогда х₁ = и – собственный вектор, соответствующий

λ₂ = 8.

Нормируем собственные векторы , получаем , . Составляем матрицу перехода от старого базиса к новому , в которой координаты нормированных собственных векторов записаны по столбцам. Выполняя преобразование

или

Найденные для х и у выражения подставим в исходное уравнение кривой:

6 · (х′ + у′)² + 2· (х′ + у′)(–х′ + у′) + 3 ·(–х′ + у′)² – 16 = 0;

2х′² + 2х′у′ + 5у′² ) + (–х′² +2х′у′ –5х′у′ + у′² )+(5х′² – 2х′у′ + 2у′² )– 16 = 0;

х′² + х′у′+ у′² – х′² – х′у′ + у′²+ х′²– х′у′+ у′²-16=0

х′² +8у′² – 16 = 0;

– каноническое уравнение эллипса.