
Вышка часть4 вариант 4
.doc
Кр10
№484
Представить
заданную функцию w=f
(z),
где z
= x
+ iy,
в виде w
= u(x,y)
+ iv(x,y);
проверить, является ли она аналитической.
Если да, то найти значение ее производной
в заданной точке z0.
![]()
![]()
Так как z=x+iy то
![]()
![]()
![]()
действительная и мнимая части функции w(x,y) имеют вид
![]()
![]()
найдем частные производные этих функций
![]()
![]()
![]()
![]()
так как
![]() и
и
![]() для любых x
и y
и эти частные производные непрерывны
на всей комплексной плоскости то функция
для любых x
и y
и эти частные производные непрерывны
на всей комплексной плоскости то функция
![]() является
аналитической на всей комплексной
плоскости
является
аналитической на всей комплексной
плоскости
![]()
![]()
======= ========= ============= ========= ================ ====
№494
Найти
все лорановские разложения данной
функции по степеням z
- z0

![]()
Представим дробь в виде сумме простейших дробей
![]()
![]()
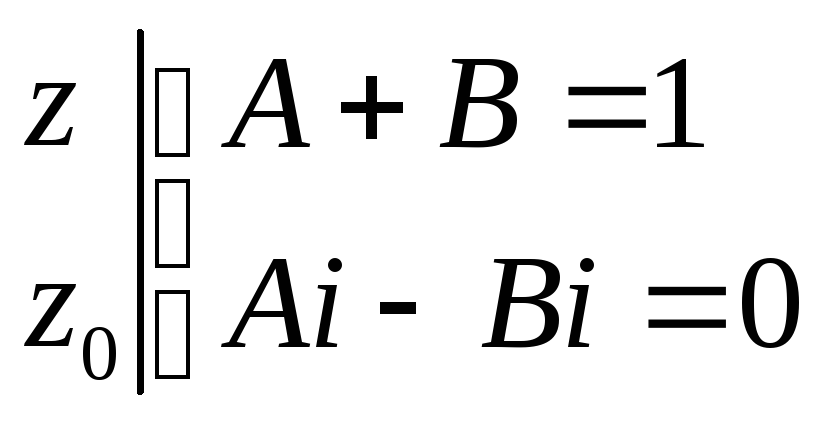

![]()
тогда

функция w(z) имеет две особые точки z=i и z=-i
Имеем три круговых
кольца с центром в точке
![]() в каждом из которых функция аналитична.
в каждом из которых функция аналитична.
1. круг
![]()
2. круг
![]()
3. круг
![]()
Найдем лорановские разложения функции в каждой из данных областей
1.
![]()
Кр10

в кольце
![]()
![]()
![]()
поэтому имеем
![]()
2.
![]()

в кольце
![]()
![]()
![]()
тогда
![]()
3.
![]()

в кольце
![]() имеем
имеем
![]()
======= ========= ============= ========= ================ ====
№504
Определить
область (круг) сходимости данного ряда
и исследовать сходимость его (расходится,
сходится условно, сходится абсолютно)
в точках z1,
z2
,
z3
.

![]()
![]()
![]()
Для данного
степенного ряда
![]() тогда
тогда
![]()
найдем радиус сходимости ряда
![]()
![]()
Область сходимости
ряда определяется неравенством |z-2|<3
которое выражает внутренность круга с
центром в точке
![]() и радиусом 3.
и радиусом 3.
Кр10
точка
![]() лежит внутри круга сходимости поэтому
ряд в этой точке расходится
лежит внутри круга сходимости поэтому
ряд в этой точке расходится
Исследуем сходимость
ряда в точке
![]() которая лежит на границе круга сходимости.
При
которая лежит на границе круга сходимости.
При
![]() получим числовой ряд
получим числовой ряд
![]()
воспользовавшись предельным признаком сравнения ,сравнив его с гармоническим рядом
![]()
![]()
![]()
![]()

следовательно
ряд
![]() также расходится.
также расходится.
Таким образом в
точке
![]() ряд расходится
ряд расходится
Ответ
В
![]() ряд сходится абсолютно
ряд сходится абсолютно
В
![]() и
и
![]() ряд расходится
ряд расходится
======= ========= ============= ========= ================ ====
№514 При помощи вычетов вычислить данный интеграл по контуру l.
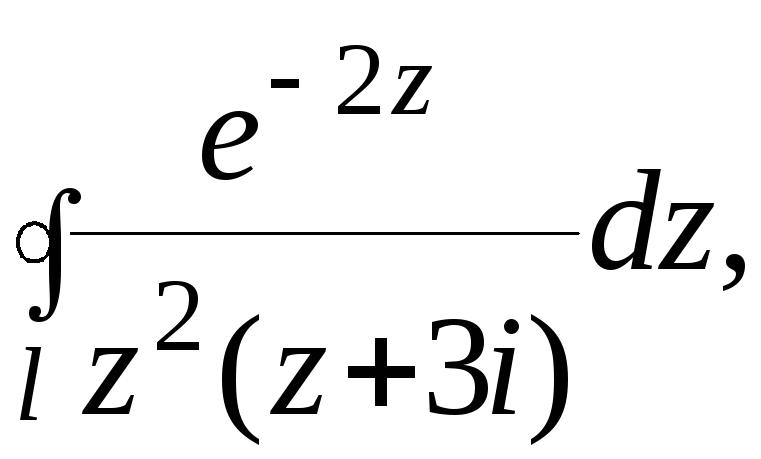
![]()
Функция внутри
контура интегрирования имеет особые
точки
![]() -полюс второго порядка и
-полюс второго порядка и
![]() -полюс первого порядка.
-полюс первого порядка.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда по основной
теореме о вычетах
![]()
![]()
