Контрольная работа №3

ВАРИАНТ №3

Контрольная работа №3

Задание 1

Построить график функции у=f(x) преобразованием графика функции у=sinx

Строим график функции у=sinx

Задание 2

Дана функция r=f(x) на отрезке 0≤φ≤2π. Требуется: 1) построить график функции в полярной системе координат по точкам, давая φ значения через промежуток π/8, начиная от φ=0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Решение:

Составим таблицу

φ	0	π/8	π/4	3/8 π	π/2	5/8 π	3/4 π	7/8 π	π
r	0,8	0,83	0,97	1,3	2	4,7	<0	<0	<0

φ	9/8π	5/4π	11/8 π	3/2π	13/8 π	7/4 π	15/8 π	2π
r	<0	<0	4,7	2	1,3	0,97	0,83	0,8

При 3 cosφ=2, r(φ)→, поэтому ; при точек линии нет так как не может быть r<0. Для вычерчивания линии проведем радиус-векторы, соответствующие углам φ, взятым с интервалом π/8. На каждом из этих радиус-векторов откладываем отрезки, равные значениям r при соответствующем значении φ из таблицы. Соединяя точки, являющиеся концами этих отрезков. получаем график данной линии.

2) Подставляя и в уравнение заданной линии, получим

Задание 3

Найти указанные пределы, не пользуясь правилом Лопиталя.

а) 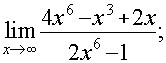б)

в) г)

Решение:

а)

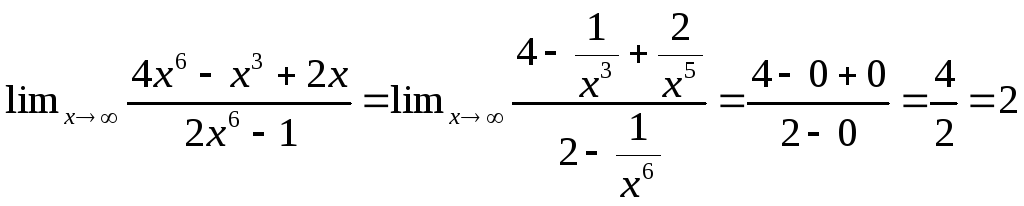
б)

в)

Задание 4

Заданы функция y=f(x) и два значения аргумента x₁ и x₂. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж.

Решение:

Функция в точке х₁ непрерывна, так как в этой точке f(x)=6, точка х₂ =3 есть точка разрыва, так как неопределенна

Значит х₂ является точкой разрыва второго рода. Чтобы сделать схематический чертеж найдем

Изобразим схематично график функции

Задание 5

Задана функция y=f(x) различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

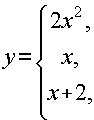
Решение:

Функция 2х² непрерывна на отрезке , функция х непрерывна на , а х+1 непрерывна значит у непрерывна на интервалах . Остается исследовать точки х₁=0 и х₂=1. Находим правые и левые пределы функции в этих точках

(правый предел)

(левый предел)

Точка х₁=0 не является точкой разрыва, так как

Исследуем точку х₂=1

(правый предел)

(левый предел)

Точка х₂=1 является точкой разрыва, так как , но существуют

Сделаем чертеж