Кр №2

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного, вечернего и дистанционного обучения

Специальность «Автоматизированные системы обработки информации»

КОНТРОЛЬНАЯ РАБОТА № 2

ПО ВЫСШЕЙ МАТЕМАТИКЕ

Электронный адрес:

Минск, 2006

52. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

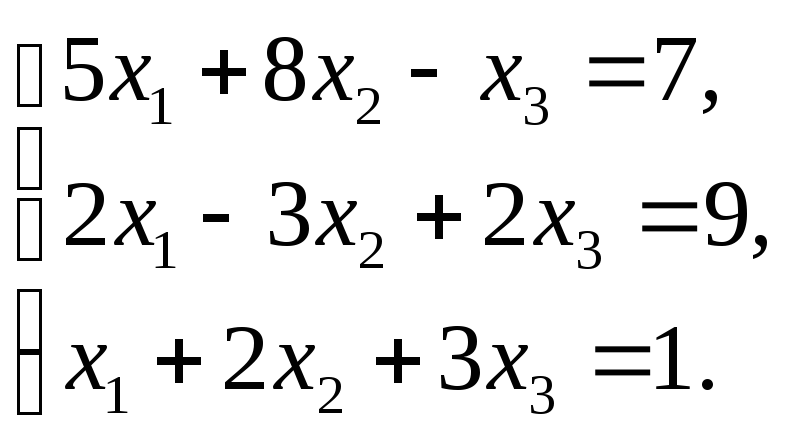
Решение:

Система является совместной, если ранг основной матрицы равен рангу расширенной матрицы. В данном случае, они равны:

Решим систему методом Гаусса. Составим расширенную матрицу

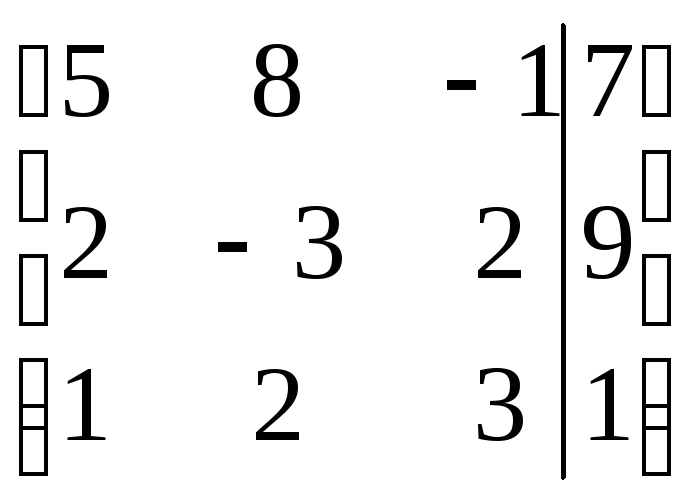и поменяем местами первую и последнюю строки:

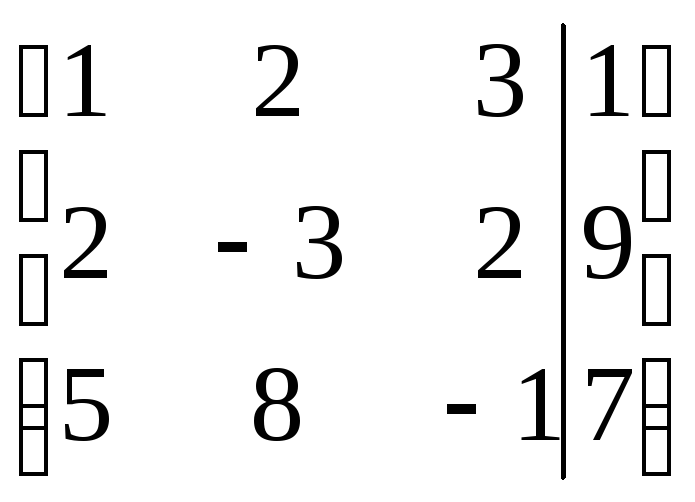
Умножим первую строку на -2 и сложим со второй, потом на -5 и сложим с третьей:

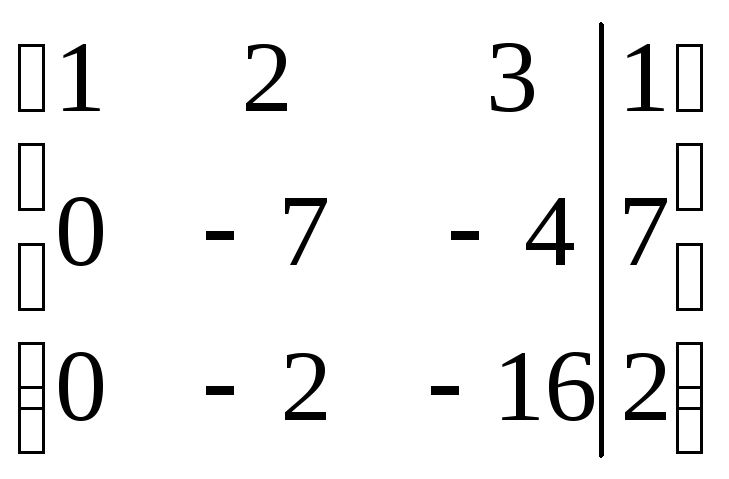
Теперь умножим вторую строку на -4 и сложим с третьей:

.

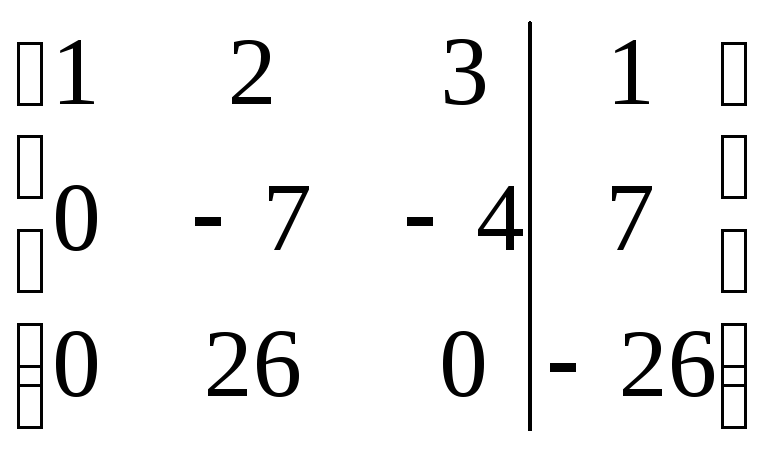Находим: .

Подставим и найдем остальные неизвестные:

, .

Решим эту задачу методом Крамера:

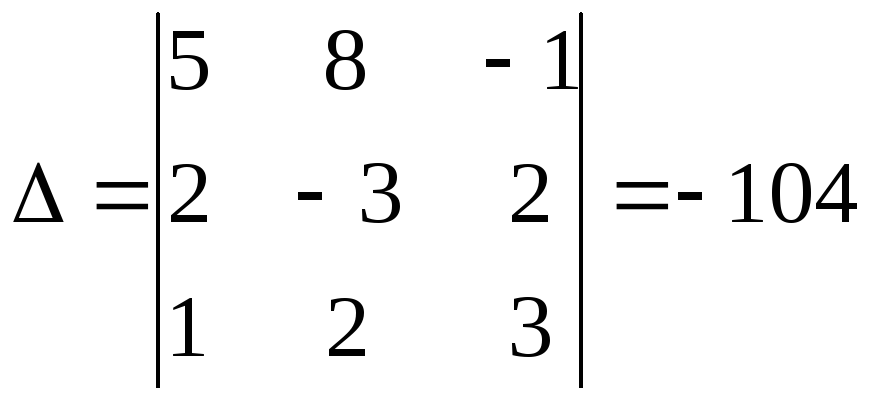– определитель

, , .

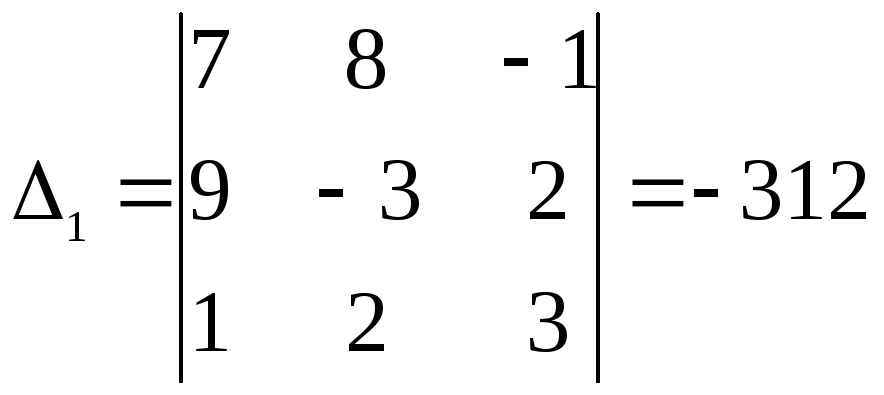
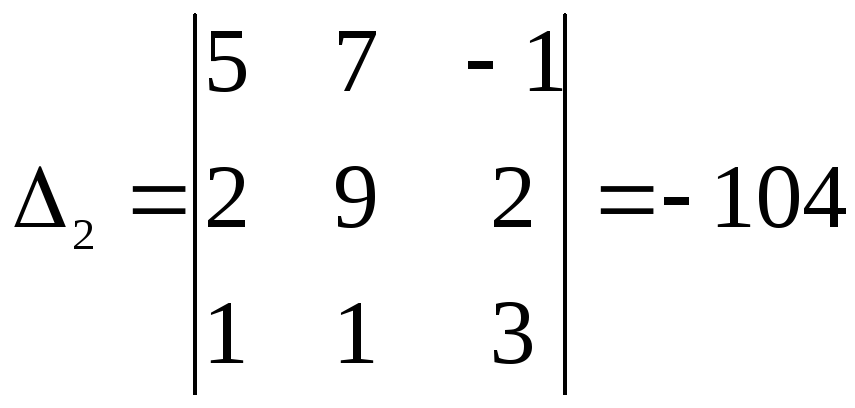
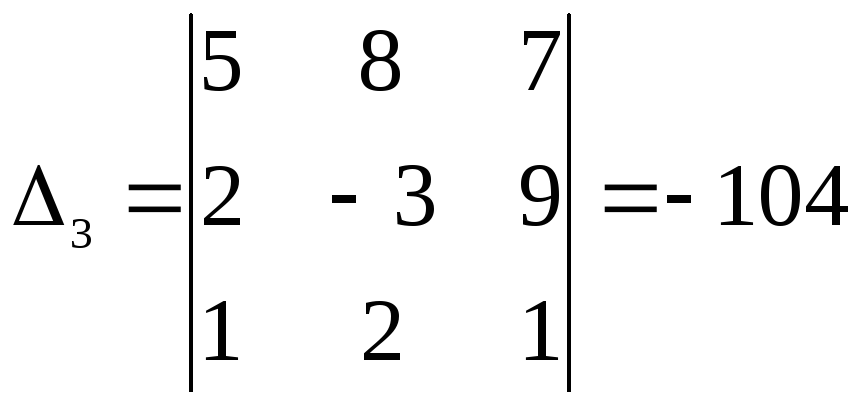
Значения, полученные разными способами решения, совпадают.

Ответ: ,,.

62. Найти размерность и базис пространства решений однородной системы линейных уравнений.

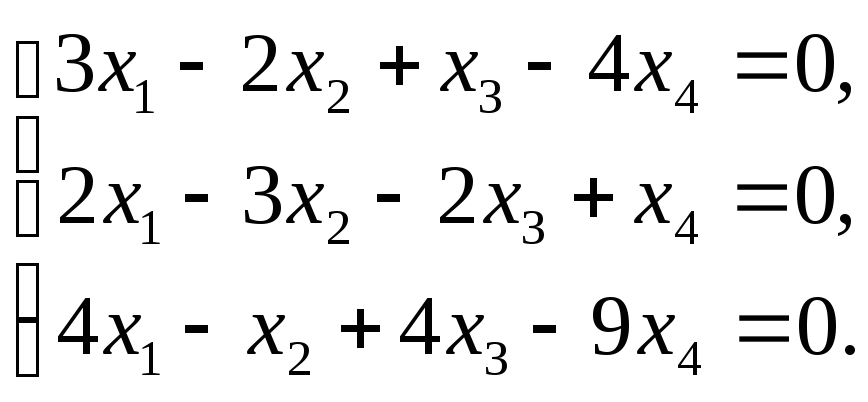
Решение:

Составим матрицу и преобразуем ее:

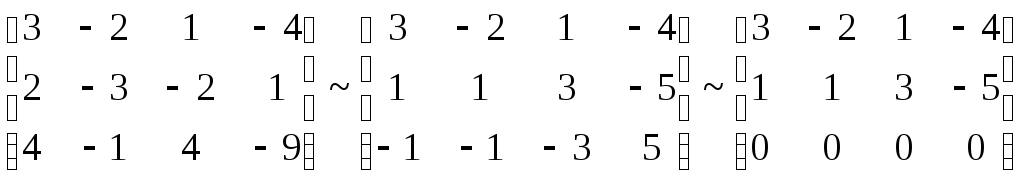
Размерность пространства решений этой системы уравнений найдем по формуле:

.

Система уравнений, эквивалентная исходной:

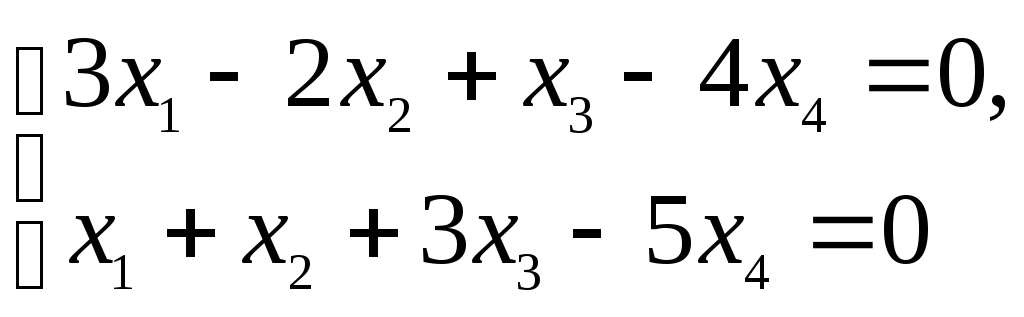
Выразим x₁ и x₂:

и .

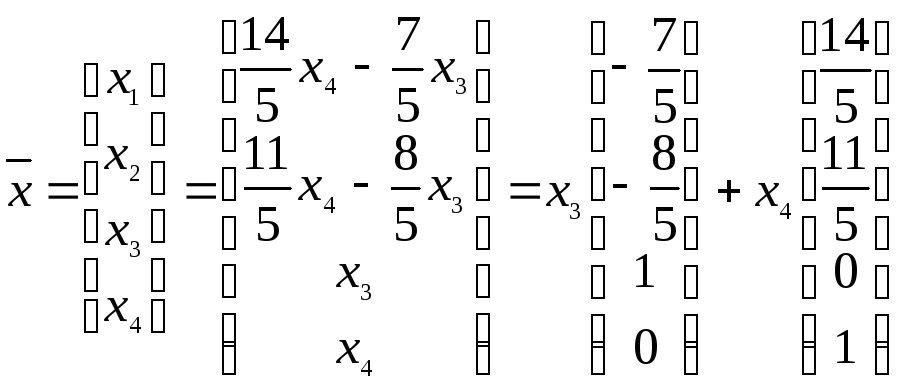, где x₃ и x₄ – произвольные числа.

Ответ: и .

7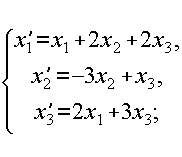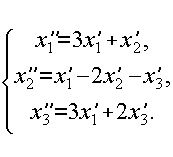2. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее через .

Решение:

Первое линейное преобразование 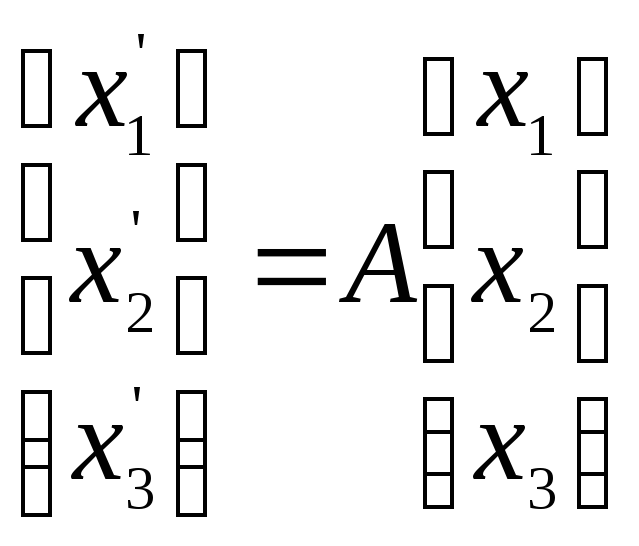имеет матрицу 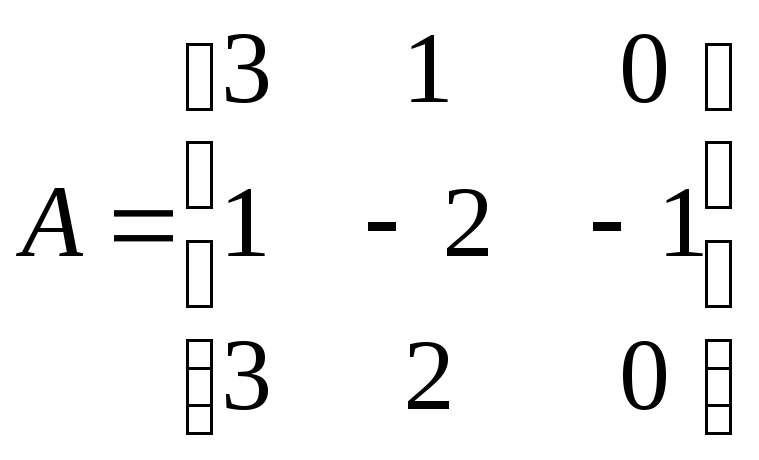, второе 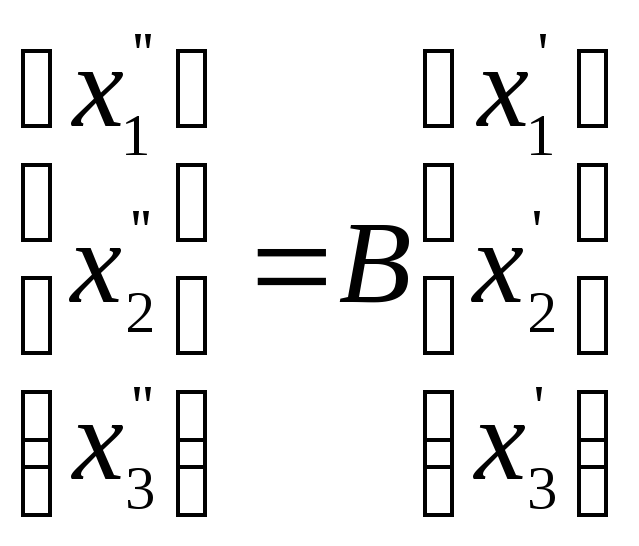имеет матрицу .

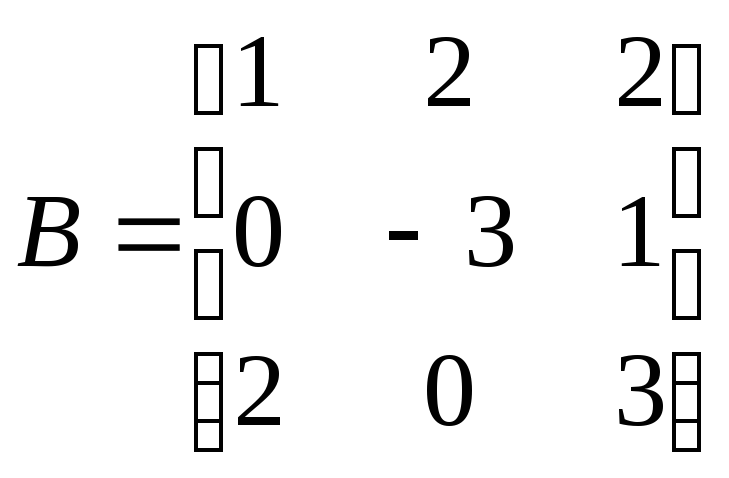Тогда произведение (т.е. последовательное выполнение) линейных преобразований имеет матрицу , т.е.:

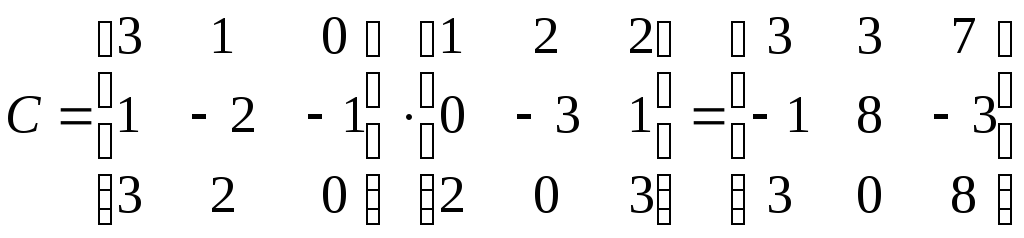
Ответ: .

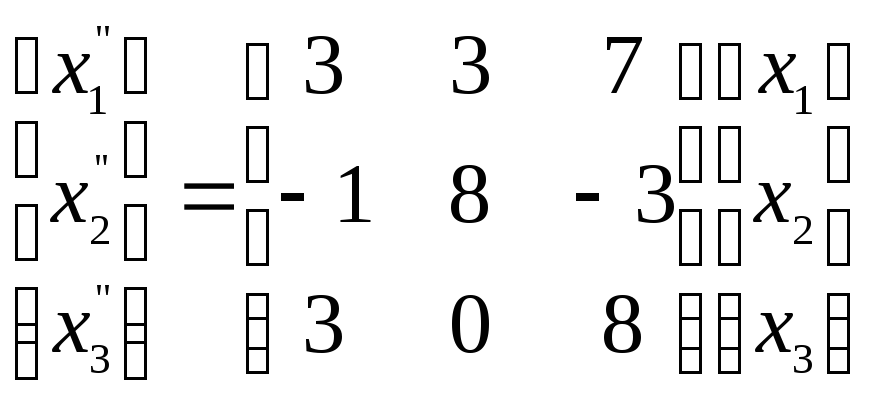82. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

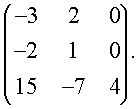
Решение:

Составляем характеристическое уравнение матрицы:

.

, ,.

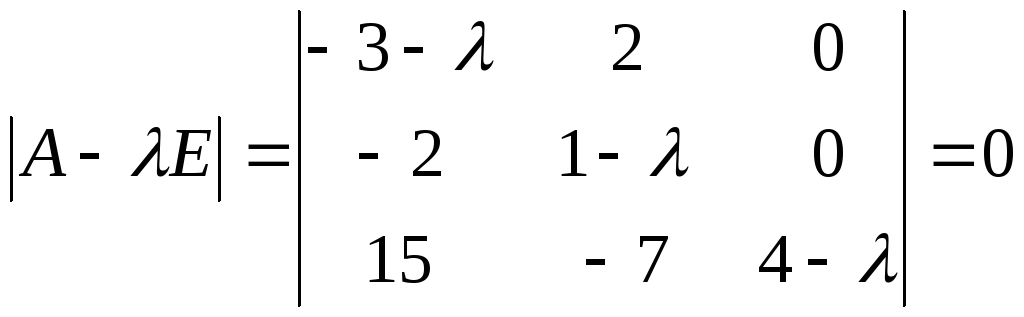При система имеет вид:

, .

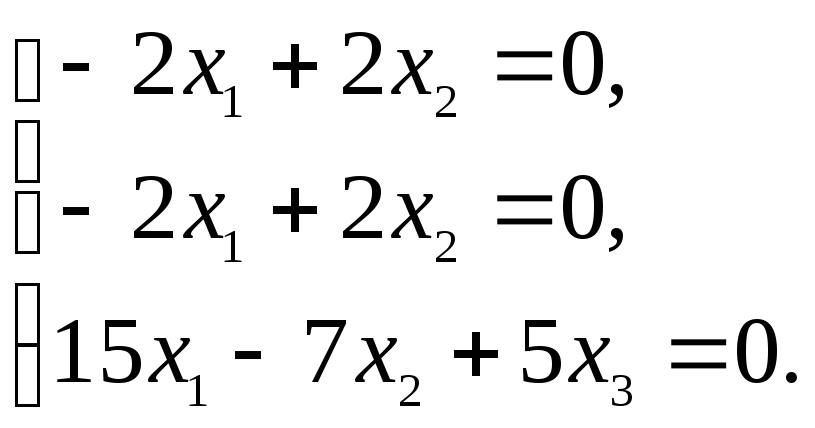
Таким образом, числу соответствует собственный вектор

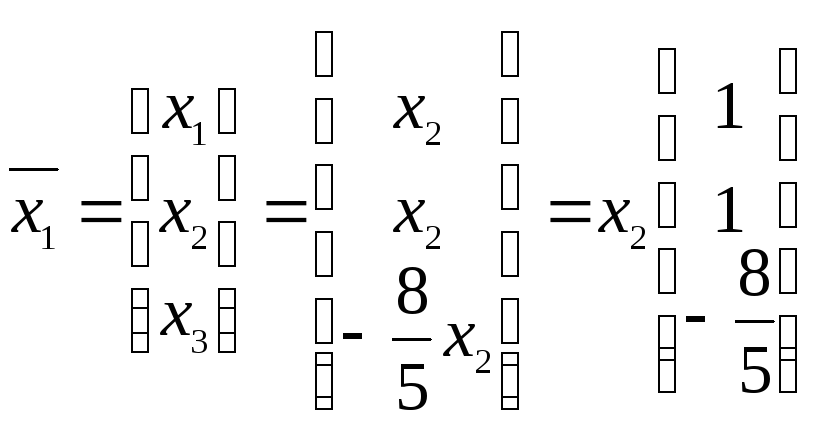
При получаем собственный вектор .

При система имеет вид:

, , .

.

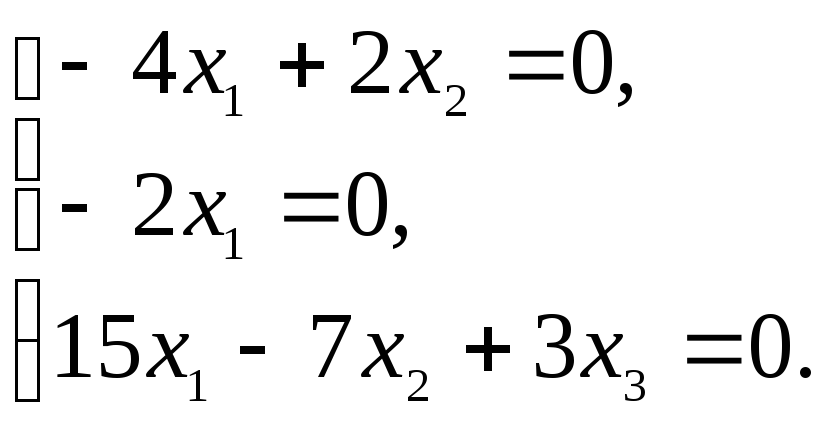
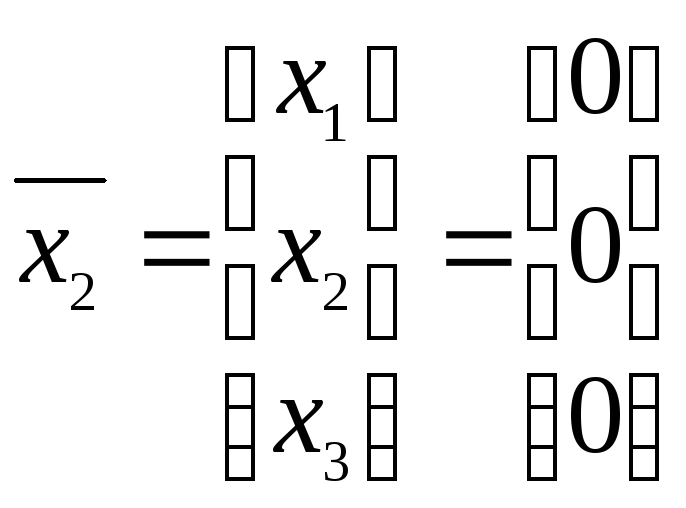
При будет система:

,

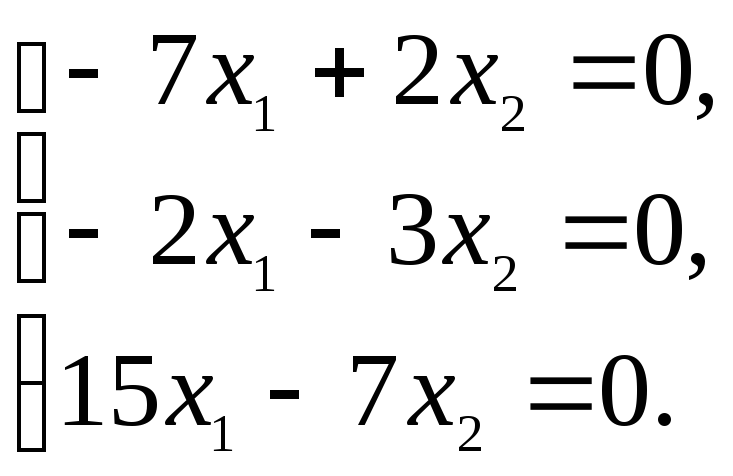
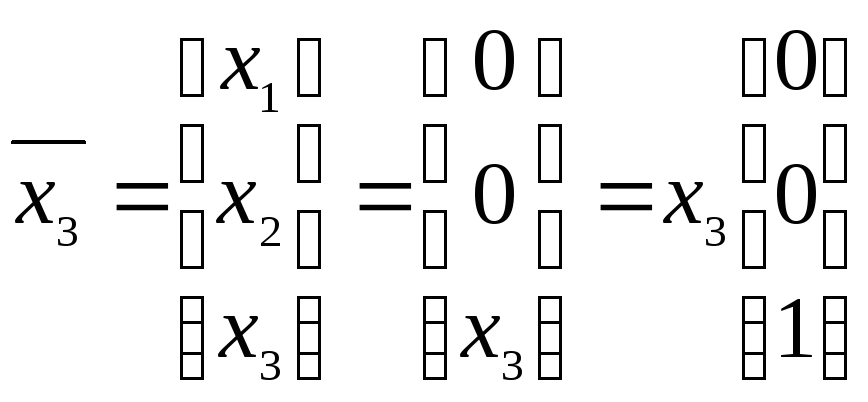
При получаем собственный вектор .

Ответ: собственные значения матрицы: , ,

Соответствующие собственные векторы , , .

92. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.

Решение:

Запишем квадратичную форму:

Решим характеристическое уравнение:

,

Найдем собственные векторы.

Для :

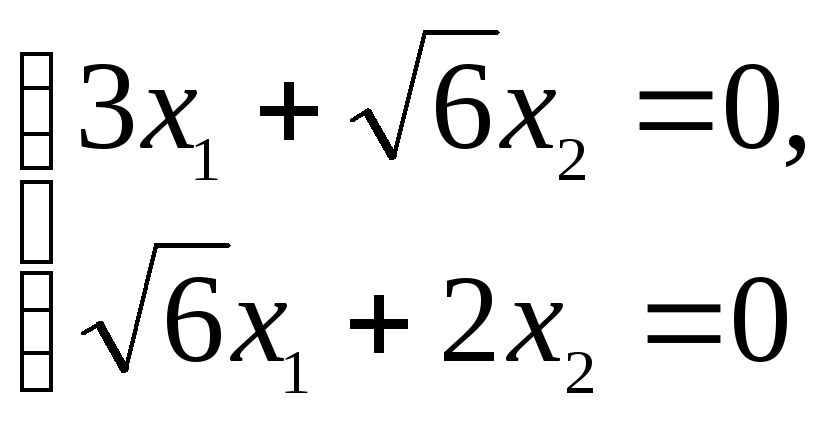
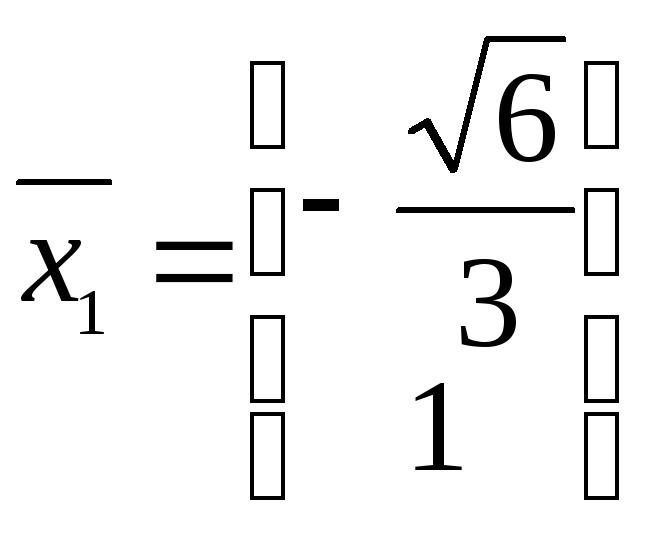
Для :

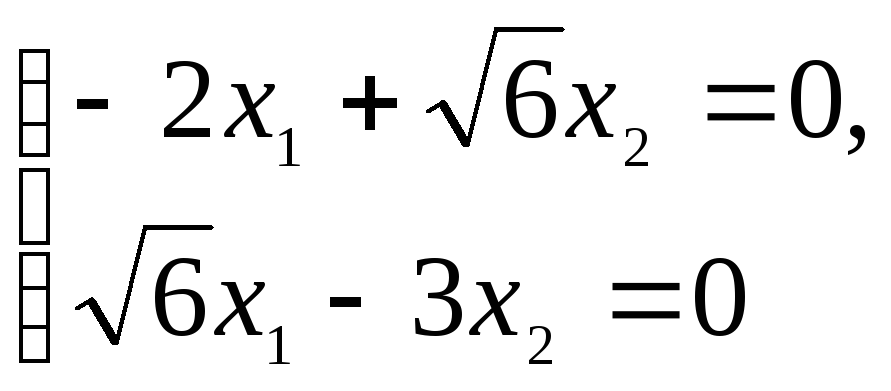
Нормируем собственные векторы по формуле:

, .

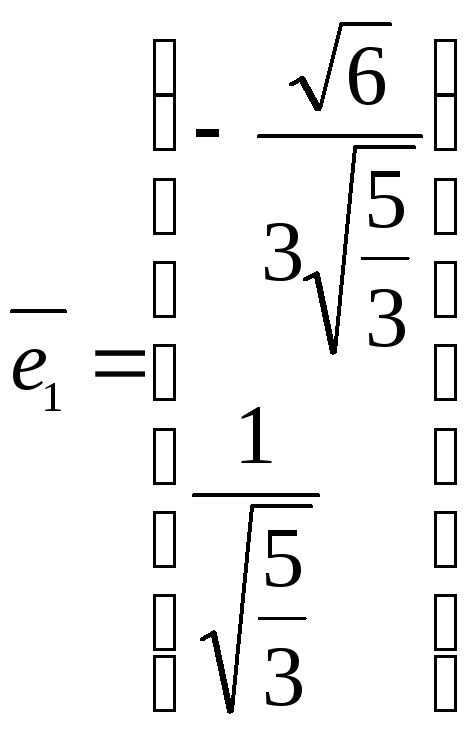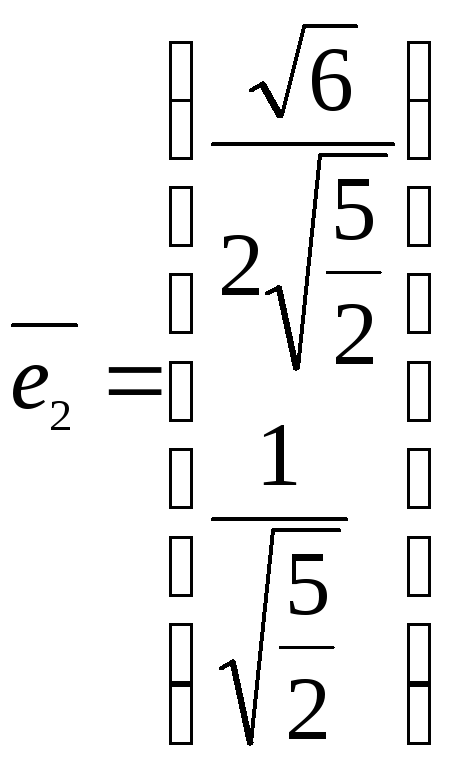Составим матрицу:

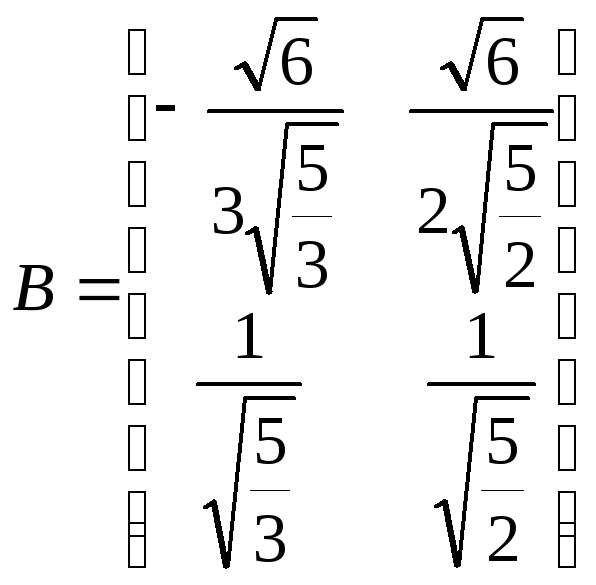
С помощью матрицы B запишем ортогональное преобразование:

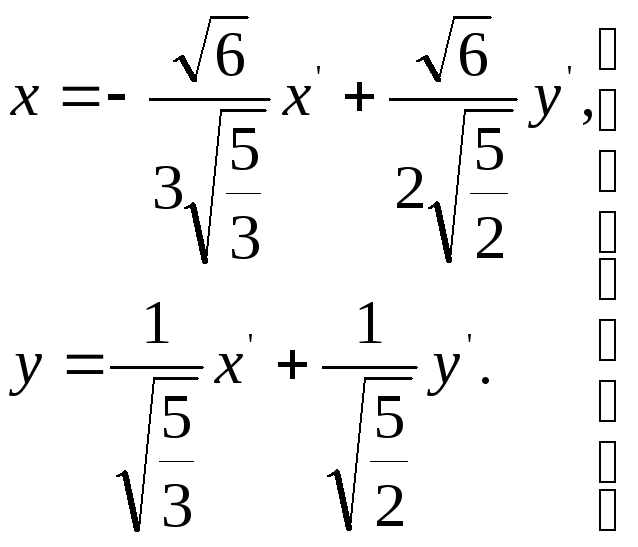
Это преобразование приводит данное уравнение в уравнение

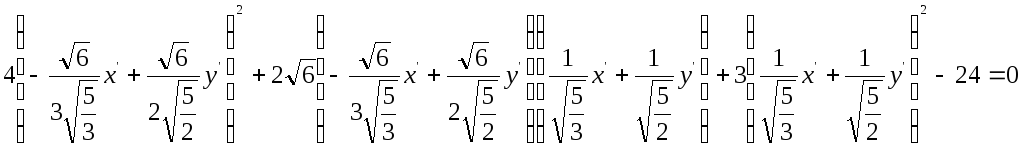
– каноническое уравнение эллипса

Ответ: