К.р. №1 2 вариант

Элементы линейной алгебры и аналитической геометрии

2. Даны векторы a(a₁; a₂; a₃), b(b₁; b₂; b₃), c(c₁; c₂; c₃) и d(d₁; d₂; d₃) в некотором базисе. Показать, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.

a (3;-5;2), b (4;5;1), c (-3;0;-4), d (-4;5;-16).

Векторы a, b, c образуют базис в пространстве R³ в том случае, если равенство a + b + c = 0 выполняется лишь тогда, когда  =  =  = 0.

Рассмотрим это условие:

(3;-5;2) + (4;5;1) + (-3;0;-4) = (0;0;0) или

Рассмотрим матрицу данной системы и приведем ее к треугольному виду:

Умножим первую строку на 5, вторую на 3 и сложим их, умножим первую строку на -2, третью на 3 и сложим их ; умножим третью строку на 7 и сложим со второй строкой .

Так как число ненулевых строк в треугольной матрице равно числу переменных, то система имеет единственное решение, а именно  =  =  = 0. Значит, векторы a, b, c образуют базис. Вектор d в базисе a, b, c имеет вид:

₁a + ₁b + ₁c = d.

В расширенном виде:

Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду (см. предыдущие действия):

Получим систему:

Значит, вектор d в базисе a, b, c имеет координаты d(1;2;5).

12. Даны координаты вершины пирамиды А₁А₂А₃А₄ .Найти:

1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

Сделать чертёж.

А₁(3;3;9), А₂(6;9;1),А₃(1;7;3), А₄(8;5;8)

1. Длина ребра А₁А₂ равна расстоянию между этими точками, которое находится по формуле : А

2. Угол между рёбрами А₁А₂ и А₁А₄ равен углу между векторами А₁А₂ и А₁А₄. Найдём координаты этих векторов.

А₁А₂ =(6-3;9-3;1-9)=(3;6;-8)

А₁А₄=(8-3;5-3;8-9)=(5;2;-1)

Тогда, если φ угол между векторами А₁А₂ и А₁А₄, то

Тогда

3. Угол между ребром А₁А₄ и гранью А₁А₂А₃ найдём следующим образом: для начала узнаем уравнение грани А₁А₂А₃, затем выпишем нормальный вектор этой грани, найдём угол между нормалью к грани А₁А₂А₃ и вектором А₁А₄. Тогда искомый угол между гранью А₁А₂А₃ и вектором А₁А₄ есть разность 90⁰ и полученного последнего угла.

Уравнение плоскости А₁А₂А₃ получим как уравнение плоскости, проходящей через три точки, а именно

или

Значит, нормальный вектор будет иметь координаты N=(-2;17;12). Найдём угол между нормалью к грани А₁А₂А₃ и вектором А₁А₄.

Тогда

Значит, угол между гранью А₁А₂А₃ и вектором А₁А₄ равен 6⁰.

4. Найдём координаты векторов А₁А₂ и А₁А₃.

А₁А₂ =(6-3;9-3;1-9)=(3;6;-8)

А₁А₃=(1-3;7-3;3-9)=(-2;4;-6)

Тогда площадь грани А₁А₂А₃ будет равна

ед²

5. Объём треугольной пирамиды равен одной шестой объема параллелепипеда, построенного на рёбрах А₁А₂ , А₁А₃, А₁А₄. Тогда

(ед³)

6. Уравнение прямой А₁А₂ имеет вид: , где (x₀;y₀;z₀ ) – координаты точки, через которую проходит прямая, а (l;m;n) – координаты направляющего вектора. За координаты (x₀;y₀;z₀ ) можно выбрать координаты точки А₁, а за направляющий вектор взять вектор А₁А₂. Тогда получим:

– уравнение прямой А₁А₂ в симметричном виде.

7. Уравнение плоскости А₁А₂А₃ было найдено в пункте 3), а именно

– уравнение плоскости в нормальном виде.

8. Высота, опущенная из вершины А₄ на грань А₁А₂А₃ имеет своим направляющим вектором нормальный вектор плоскости А₁А₂А₃ , а значит

- уравнение высоты в симметричном виде.

Сделаем чертёж.

22. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(3;0) чем от оси ординат.

Пусть M(x;y) – произвольная точка искомой кривой. Найдем нужные расстояния:

d = = – расстояние от точки А(3;0) до произвольной точки кривой;

d = = = – расстояние от произвольной точки кривой до оси ординат. Тогда

или ;

Это гипербола с полуосями а= 0 и b= центром в точке (-1;0).

32. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

1) Для решения системы методом Гаусса рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:

= [поменяем местами первую и третью строки]= = [умножаем первую строчку на -2 и складываем со второй, умножаем первую на -5 и складываем с третьей ] = = [умножаем третью строку на 7, вторую на -2 и складываем их] =

Ранг расширенной матрицы равен числу ненулевых строк, т.е. равен 3. Теперь рассмотрим матрицу А и приведём её к треугольному виду аналогичными действиями:

.

Ранг матрицы равен числу ненулевых строк, т.е. равен 3. Так как ранг матрицы системы совпадает с рангом расширенной матрицы, то система совместна.

Тогда получим систему:

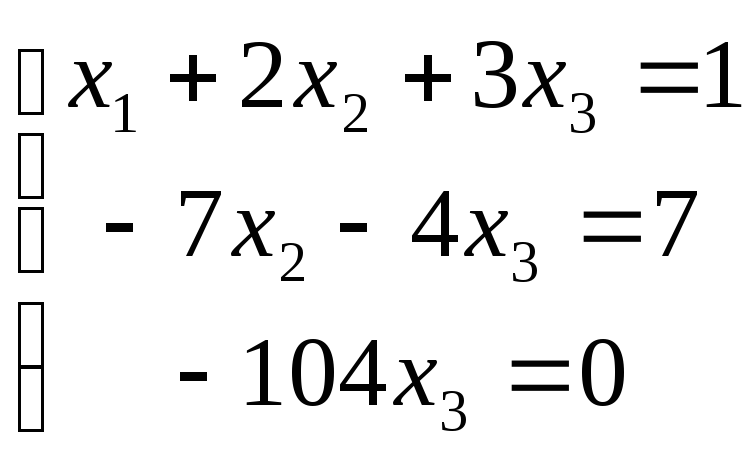
Тогда получим решение:

x₃ = 0; x₂ = -1; x₁ =3.

2) Для решения матричным методом нужно рассмотреть матричное уравнение: AX = B, где A = , X = , B = .

Тогда X = A^-1B.

Вычислим обратную матрицу .

Тогда A^-1 =

Получим X = A^-1B == = .

42. Найти размерность и базис пространства решений однородной системы линейных уравнений

Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:

= [умножаем первую строчку на -2, вторую на 3 и складываем их, умножаем первую на -4, третью на 3 и складываем их] = = [ складываем вторую строку с третьей] = .

Ранг расширенной матрицы равен числу ненулевых строк, т.е. равен 2. Теперь рассмотрим матрицу А и приведём её к треугольному виду аналогичными действиями:

.

Ранг матрицы равен числу ненулевых строк, т.е. равен 2. Так как ранг матрицы системы совпадает с рангом расширенной матрицы, то система совместна.

Тогда получим систему:

Пусть х₃=t, х₄=s тогда получим решение:

х₄=s, x₃ = t; x₂ =; x₁ = .

52. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матриц.

Характеристическое уравнение имеет вид:

₁=-1, ₂=-1, ₃=4 – собственные значения линейного преобразования.

Для ₁=-1 и ₂=-1 найдём собственный вектор.

Собственный вектор для ₁=-1 и ₂=-1 имеет вид (0;0;0).

Для ₃=4 найдём собственный вектор.

.

Собственный вектор для ₃=4 имеет вид (0;0; 0).

62. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм

Запишем данное уравнение в виде:

Найдём матрицу Т ортогонального оператора, приводящего данную квадратичную форму к каноническому виду.

Запишем характеристическую матрицу:

Её корнями являются значения ₁=1, ₂=6.

Для ₁=1 найдём собственный вектор.

, где t – любое число.

Собственный вектор-столбец для ₁=1 имеет вид . Тогда есть нормированный собственный вектор-столбец.

Для ₂=7 найдём собственный вектор.

, где s – любое число.

Собственный вектор-столбец для ₂=6 имеет вид . Тогда есть нормированный собственный вектор-столбец.

Ортогональный оператор, приводящий квадратичную форму к каноническому виду, имеет матрицу .

Базисными векторами новой системы координат являются:

В системе координат уравнение данной фигуры примет вид:

Это эллипс, центр которого находится в точке (0,0) относительно системы координат , а оси симметрии параллельны координатным осям этой системы.