
К.р. №1 5 вариант
.docx|
|
|
|
|
|
|
|
|
Задача 5. Даны
4 вектора
 ,
,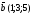 ,
, и
и
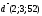 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
 в этом базисе.
в этом базисе.
Решение
Базисом в пространстве
 являются
любые три некомпланарных вектора.
Условием компланарности трех векторов,
заданных в декартовой системе координат,
является равенство их смешанного
произведения нулю. Отсюда находим:
являются
любые три некомпланарных вектора.
Условием компланарности трех векторов,
заданных в декартовой системе координат,
является равенство их смешанного
произведения нулю. Отсюда находим:

Значит, векторы
 некомпланарны и образуют базис. Составим
систему уравнений в координатном виде
некомпланарны и образуют базис. Составим
систему уравнений в координатном виде ,
где
,
где
 координаты вектора
координаты вектора
 в базисе
в базисе
 ,
и найдем
,
и найдем
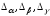 .
.
Определитель
 найден выше:
найден выше:
 .
.
 ;
;
 ;
;
 .
.
Имеем:
 ;
;  ;
;  .
.
Значит,
 .
.
Задача 15.Даны координаты вершин пирамидыА1А2 А3А4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани пирамиды А1А2 А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2 А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2 А3. Сделать чертеж.
 ;
;  ;
;  ;
;  .
.
Решение
1) Длина ребра
 численно равна расстоянию между точками
численно равна расстоянию между точками
 и
и
 ,
которое в декартовой системе координат
вычисляется по формуле
,
которое в декартовой системе координат
вычисляется по формуле
 ,
,
где
 координаты точки
координаты точки
 ,
,
 координаты точки
координаты точки
 .
.
Таким образом, вычисляем:
 .
.
2)Угол
между ребрами
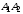 и
и
 вычисляется по формуле
вычисляется по формуле
 из скалярного произведения векторов
из скалярного произведения векторов
 и
и
 .
.
Находим:
 ;
;
 ;
;
 ;
; ;
;
 .
.
Поэтому
 ,
, .
.
3) Угол
между ребром
 и плоскостью
и плоскостью
 –
это угол между вектором
–
это угол между вектором
 и его ортогональной проекцией
и его ортогональной проекцией
 на грань
на грань
 .
.

Вектор
 перпендикулярен грани
перпендикулярен грани
 ,
что вытекает из определения векторного
произведения векторов
,
что вытекает из определения векторного
произведения векторов
 и
и
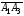

Вектор
 перпендикулярен грани
перпендикулярен грани
 ,
что вытекает из определения векторного
произведения векторов
,
что вытекает из определения векторного
произведения векторов
 и
и

 :
: 
Здесь
 ,
,
 .
Находим:
.
Находим:
 .
.
Отсюда
получаем, что
 .
.
4) Площадь грани
 находим, используя геометрический смысл
векторного произведения:
находим, используя геометрический смысл
векторного произведения:
 .
.
5) Объем пирамиды
 численно равен одной шестой модуля
смешанного произведения векторов
численно равен одной шестой модуля
смешанного произведения векторов
 ,
,
 ,
, ,
котороенаходится по формуле
,
котороенаходится по формуле
 .
.
Таким
образом, .
.
6) Для составления уравнений
прямой
 воспользуемся формулой:
воспользуемся формулой:
 ,
где
,
где
 координаты точки
координаты точки
 ,
,
 координаты точки
координаты точки
 .
Тогда
.
Тогда
 .
.
В таком виде уравнения прямой называются каноническими. Они могут быть записаны и в виде
 или
или 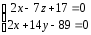
т.е. уравнение прямой как линии пересечения двух плоскостей.
7) Для составления уравнения
плоскости
 воспользуемся формулой
воспользуемся формулой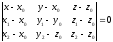 ,
где
,
где
 координаты точки
координаты точки ,
,
 координаты точки
координаты точки ,
,
 координаты точки
координаты точки .
.
 .
.
8) Искомое уравнение высоты
получим из канонических уравнений
прямой
 ,
где
,
где
 точка, лежащая на искомой прямой;
точка, лежащая на искомой прямой;
 координаты вектора
координаты вектора
 ,
параллельного искомой прямой. При этом
в качестве точки
,
параллельного искомой прямой. При этом
в качестве точки
 возьмем точку
возьмем точку
 ,
а в качестве вектора
,
а в качестве вектора
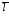 возьмем нормальный вектор плоскости
возьмем нормальный вектор плоскости
 ,
т.е.
,
т.е.
 .
Имеем
.
Имеем
 .
.

Задача 25. Составить
уравнение линии, каждая точка которой
является центром окружности, касающейся
оси абсцисс и проходящей через точку .
.
Решение
Обозначим произвольную точку
искомой линии как .
Тогда по условию получаем, что
.
Тогда по условию получаем, что ,
где Р –точка на оси
абсцисс.P(x;0)
Находим:
,
где Р –точка на оси
абсцисс.P(x;0)
Находим:
 ;
;
 .
.
Значит,
 .
Возводя обе части этого соотношения в
квадрат, получаем уравнение линии
.
Возводя обе части этого соотношения в
квадрат, получаем уравнение линии
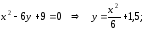 .
.
Уравнение параболы.
Задача 35. Доказать совместимость данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления:

Решение
Система, имеющая хотя бы одно решение, называется совместной.
Составим матрицу коэффициентов (основную матрицу системы) и найдем её определитель:
 .
.
Так как определитель отличен от нуля, то система совместна и имеет единственное решение.
1) При решении системы линейных уравнений методом Гаусса действия производятся над расширенной матрицей.
Составим расширенную матрицу
системы:
 .
.
Теперь приведём её путем
элементарных преобразований к треугольному
или трапециевидному виду. Для этого
прибавим к 3‑ей строке 1‑ю, умноженную
на ,
ко 2‑ой строке прибавим 3‑ю,
умноженную на
,
ко 2‑ой строке прибавим 3‑ю,
умноженную на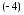 .
Получим:
.
Получим:
 .
.
Ко 2‑й строке прибавим 3‑ю, умноженную на (-7) и переставим местами 2-ю и 3-ю строки, получим
 .
.
Таким образом, ранги основной и расширенной матриц равны 3. Система совместна и имеет единственное решение. Она сводится к эквивалентной системе линейных уравнений

Отсюда, подставляя
 во второе уравнение, получим
во второе уравнение, получим
 ,
а из первого уравнения
,
а из первого уравнения
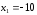 .
Итак,
.
Итак,
 ,
,
 ,
,
 .
.
2) Определитель основной
матрицы системы
 ,
значит, система совместна и для матрицы
коэффициентов существует обратная
матрица. Находим решение по формуле
,
значит, система совместна и для матрицы
коэффициентов существует обратная
матрица. Находим решение по формуле
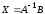 или
или
 ,
,
где
 ,
,
 алгебраические дополнения элементов
алгебраические дополнения элементов
 матрицы А:
матрицы А:
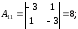



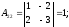




Таким образом, обратная матрица к основной матрице системы имеет вид
 .
.
Проверим правильность вычисления обратной матрицы: исходя из определения обратной матрицы, находим

Значит, матричное решение системы имеет вид

Отсюда следует, что
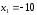 ,
,
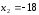 ,
,
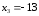 .
.
Задача 45. Найти размерность и базис пространства решений однородной системы линейных уравнений.

Решение
Находим ранг матрицы:

Отсюда
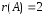 .
.
Таким образом, в данной системе
линейных уравнений 2 зависимых и
 независимая переменные. Перенося
слагаемые с х3и х4 в
правую часть (базисный минор образован
коэффициентами при х1, х2),
по последней матрице записываем систему
независимая переменные. Перенося
слагаемые с х3и х4 в
правую часть (базисный минор образован
коэффициентами при х1, х2),
по последней матрице записываем систему
 -базисный минор
-базисный минор

Итак, общее решение однородной системы линейных уравнений

Отсюда следует, что
вектор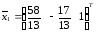 и
и являются
решениями однородной системы
являются
решениями однородной системы .
Обозначив произвольную константу х3
через
.
Обозначив произвольную константу х3
через
 ,а
х4через
,а
х4через
 ,
получим общее решение системы в виде
,
получим общее решение системы в виде .
.
Задача 55. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:

Решение
Составляем характеристическое уравнение матрицы А и находим его корни:


Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.
При
 система
система
 имеет вид:
имеет вид:

Значит, собственному значению
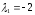 соответствует собственный вектор
соответствует собственный вектор
 .
.
Здесь х3 – произвольное
действительное число, не равное нулю.
Положив его, в частности, равным единице,
получим собственный вектор в виде
 .
.
Аналогично при
 система
система
 имеет вид:
имеет вид:

Значит, собственному значению
 соответствует собственный вектор
соответствует собственный вектор
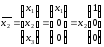 .
.
Здесь х2 – произвольное
действительное число, не равное нулю.
Соответствующий собственный вектор
имеет вид
 .
.
Аналогично при
 система
система
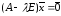 имеет вид:
имеет вид:

Значит, собственному значению
 соответствует собственный вектор
соответствует собственный вектор
 .
.
Приняв
 ,
получим собственный вектор в виде
,
получим собственный вектор в виде
 .
.
Таким образом, матрица А
имеет три собственных значения
 ,
,
 ,
,
 ,
а собственные векторы имеют вид
,
а собственные векторы имеют вид
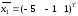 ;
; ;
;
Задача 65. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм:
 .
.
Решение
Составим матрицу данной
квадратичной формы
 и найдём её собственные значения:
и найдём её собственные значения:
 .
.
Корнями характеристического
уравнения являются числа
 и
и
 .
Им соответствуют собственные векторы
.
Им соответствуют собственные векторы
 и
и
 .
.
Нормируя собственные векторы, получим
 и
и
 .
.
Матрица перехода Т к новому базису имеет вид
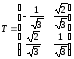 .
.
Вводим замену переменных

Подставим эти выражения в исходное уравнение кривой:


После преобразования выражения получили
 ,
,
Разделим на 15 правую и левую части полученного уравнения:
 в
системе координат
в
системе координат
 .
.
Полученное
уравнение является уравнением эллипса
с полуосями

