
контр№5
.docБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет НиДО
Специальность ПОИТ
Контрольная работа №5
по дисциплине «Высшая математика»
часть 2
Вариант № 3
Выполнил студент: **************
Группа ******
Зачетная книжка *****
Минск 2011
Задания 213
Дана
функция
![]() Показать, что
Показать, что
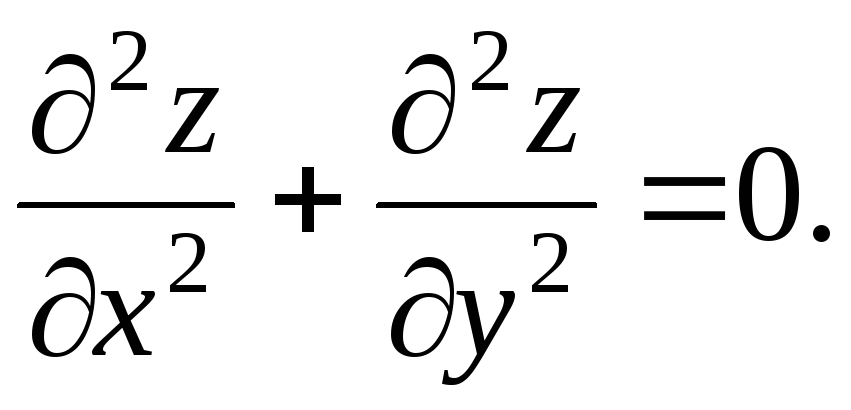
Решение. Найдем
частные производные
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() .
.
![]()
![]()
Подставим их в уравнение
![]()
Получим тождество. Следовательно, функция z удовлетворяет данному уравнению.
Задание 223
Дана
функция
![]() и
две точки А
(-2; 2) и В
(-2,02; 2,05). Требуется: 1) вычислить значение
z1
и
две точки А
(-2; 2) и В
(-2,02; 2,05). Требуется: 1) вычислить значение
z1![]() функции
в точке В;
2) вычислить приближенное значение
функции
в точке В;
2) вычислить приближенное значение
![]() функции в точке В
исходя из значения z0
функции
в точке А, заменив приращение функции
при переходе от точки А
к точке В
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z=f(x,
y)
в
точке С
(x0,
y0,
z0).
функции в точке В
исходя из значения z0
функции
в точке А, заменив приращение функции
при переходе от точки А
к точке В
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z=f(x,
y)
в
точке С
(x0,
y0,
z0).
Решение. 1.
![]()
2.
![]() .
.
Итак,
![]()
![]() ;
;
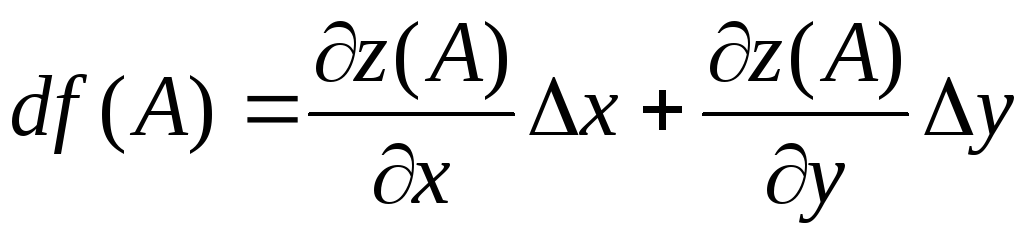 .
.
Найдем
![]() .
.
![]() ,
,
![]() ,
;
,
;
![]()
![]()
f(-2.02;2.05)=12+(-5)*(-0.02)+5*0.05=12.35
3.
Уравнение касательной плоскости к
поверхности, заданной уравнением
F(x;y;z)=0,
в точке C(x0;y0;z0)
записывается
в виде: ![]() .
Так
как в условии задачи уравнение поверхности
задано в явном виде, то сначала его
необходимо преобразовать к виду
F(x;y;z)=0:
.
Так
как в условии задачи уравнение поверхности
задано в явном виде, то сначала его
необходимо преобразовать к виду
F(x;y;z)=0:
![]()
Теперь
найдем частные производные ![]() :
:
![]()
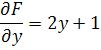
![]()
Вычислим значения частных производных первого порядка в точке C(-2;2;12):
![]()
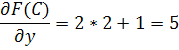
![]()
Подставим полученные значения в уравнение касательной плоскости:
![]()
-5x+5y-z-8=0
Задание № 233
Исследовать
на экстремум функции двух переменных
![]()
Решение. Найдем частные производные и составим систему уравнений для нахождения стационарных точек:
![]() ,
,
![]() ,
,
то система для отыскания стационарных точек имеет вид
![]() .
.
Решив систему, получим одну стационарную точку P(0;0). Найдем производные 2-го порядка
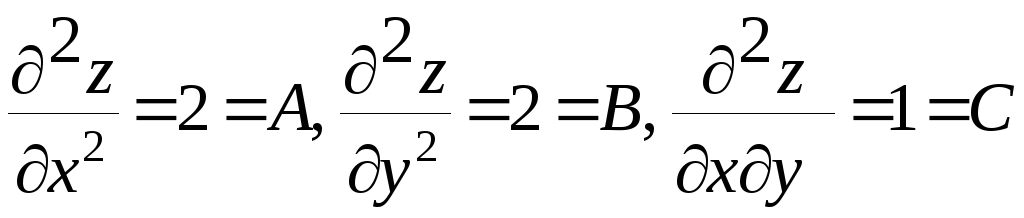
и
составим дискриминант
![]() для
стационарной точки.
для
стационарной точки.
Получим
P(0,0)
Δ=4-1>0, A>0
в
P(0;0)
функция имеет минимум,
![]()
Задание 243
Дана
функция
![]() ,
точка А
(1; 3) и вектор а = -5i
+ 12j.
,
точка А
(1; 3) и вектор а = -5i
+ 12j.
Найти:
1) grad z в точке А;
2) производную в точке А в направлении вектора а.
Решение. 1.![]()
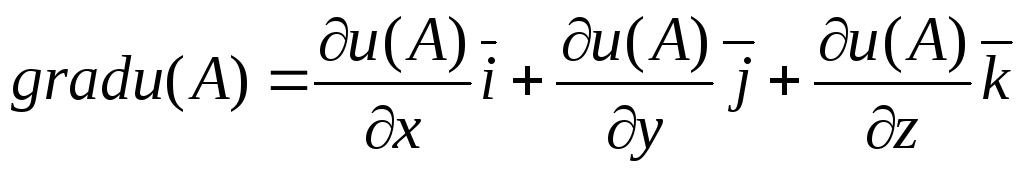 .
Найдем частные производные функции u
в точке А.
.
Найдем частные производные функции u
в точке А.
![]() ;
;
![]() ;
;
Тогда
![]() .
.
2.
Производную по направлению вектора
![]() в точке А
находим по формуле
в точке А
находим по формуле
![]()
Частные
производные в точке А нами уже найдены.
Для того чтобы найти
![]() ,
найдем единичный вектор
,
найдем единичный вектор
![]() вектора
вектора
![]() .
.
![]() ,
где
,
где
![]() .
.
Отсюда
![]() .
.
Получим
![]()
Задание №253
Найти условный экстремум функции при помощи функции Лагранжа.
![]() при
при
![]()
Решение. Составляем функцию Лагранжа:
![]()
Имеем
![]()
![]()
Необходимые условия дают систему
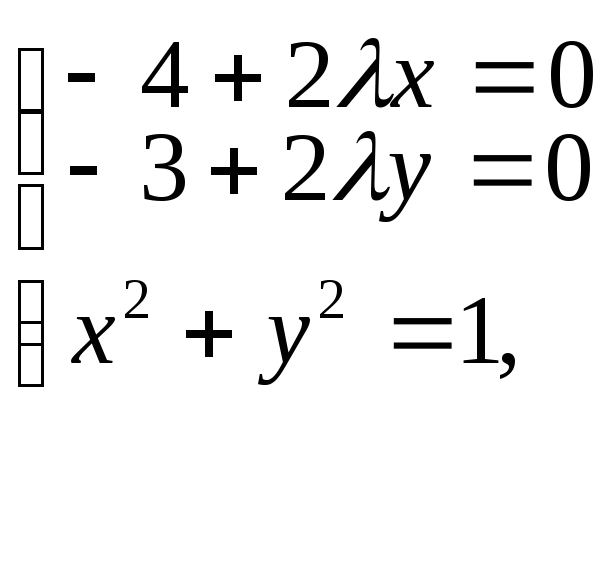
Решив которую, найдем:
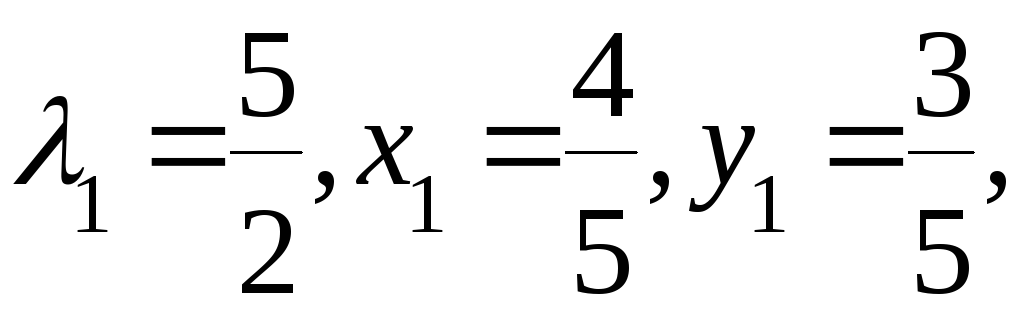
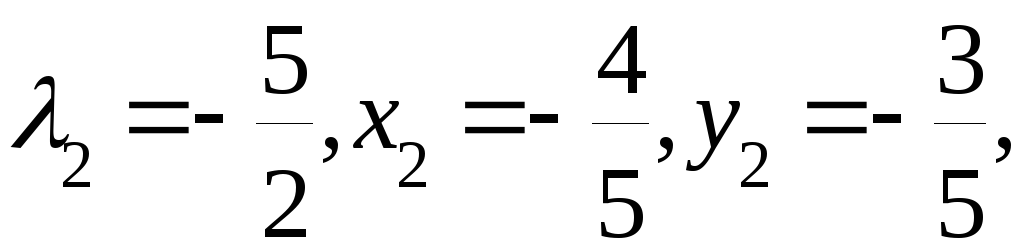
Находим
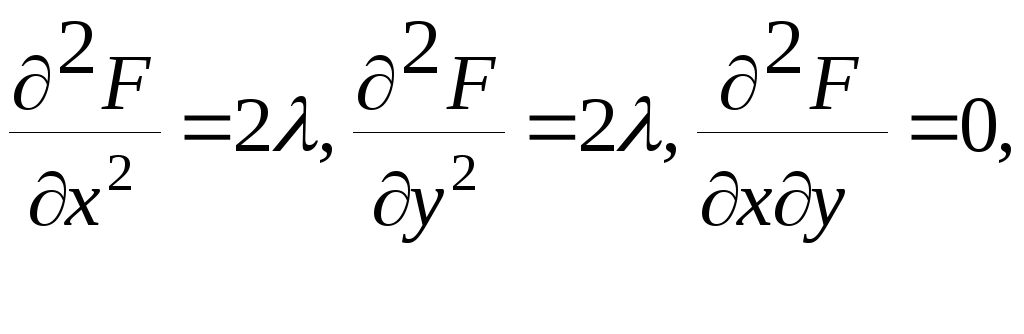
![]()
При

![]() в этой точке условный минимум,
в этой точке условный минимум,
![]()
При
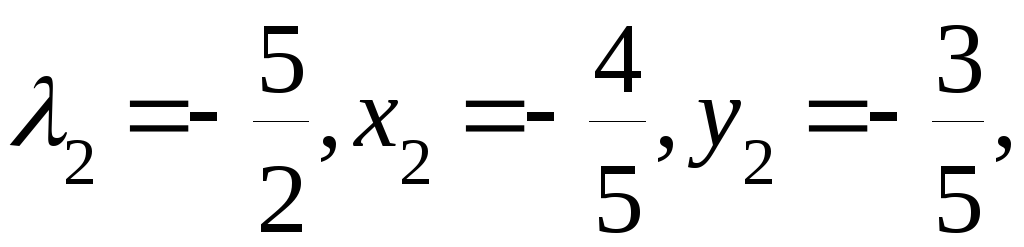
![]() в этой точке условный максимум,
в этой точке условный максимум,
![]()
