
математика кр3ариант 8
.docучреждения образования
белорусский государственный университет
информатики и радиоэлектроники
факультет заочного и дистанционного обучения
программное обеспечение информационных технологий
контрольная работа №3
по высшей математике
вариант №8
1. Выделив в заданной функции полный квадрат, получить уравнение параболы и построить её график.
![]()
Решение:
![]() ;
;
В
результате выделения полного квадрата
в исходной функции получили уравнение
параболы вида:![]() .
.
Для данной функции построим график (смотри рисунок 1.1):
Таблица
1– Значения x
и y
для функции
![]()
-
x
2
1
3
0
4
1,5
2,5
y
-1
-4
-4
-13
-13
-1,75
-1,75

Рисунок 1.1 – График
функции
![]()
2. Задана функция
![]() на отрезке
на отрезке
![]() .
Требуется: 1) построить
график функции в полярной системе
координат по точкам, давая аргументу
.
Требуется: 1) построить
график функции в полярной системе
координат по точкам, давая аргументу
![]() значения через промежуток
значения через промежуток
![]() ;
2) найти каноническое
уравнение полученной линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью, и по
уравнению определить тип линии.
;
2) найти каноническое
уравнение полученной линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью, и по
уравнению определить тип линии.
![]()
Решение
Т.к
полярный радиус неотрицателен, т.е.
![]() то
то
![]() ,
,
![]() ,
откуда заключаем, что
,
откуда заключаем, что
![]()
Составим вспомогательную таблицу
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
0,92 |
0,71 |
0,38 |
0 |
-0,38 |
-0,71 |
-0,92 |
-1 |
-0,92 |
-0,71 |
-0,38 |
0 |
0,38 |
0,71 |
0,92 |
1 |
|
|
1 |
1,03 |
1,11 |
1,26 |
1,5 |
1,85 |
2,32 |
2,79 |
3 |
2,79 |
2,32 |
1,85 |
1,5 |
1,26 |
1,11 |
1,03 |
1 |
Для
построения кривой на луче, проведенном
из полюса под углом
![]() ,
,
откладываем
соответствующее значение полярного
радиуса
![]() и
и
соединяем полученные точки.

Найдем
уравнение кривой
![]() в прямоугольной системе координат.
в прямоугольной системе координат.
Для
этого заменим
![]() и
и
![]() их выражением через
их выражением через
![]() и
и
![]() по формулам,
по формулам,
![]() ,
,
![]() =
=![]()
Итак получаем:


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Получаем уравнение эллипса.
3. Найти указанные пределы, не пользуясь правилом Лопиталя.
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() .
.
1) Решение:
![]() =
=
![]() ;
;
Имеем неопределенность вида
![]() .
Разделим числитель и знаменатель дроби
на наибольшую степень, то есть на
.
Разделим числитель и знаменатель дроби
на наибольшую степень, то есть на
![]() :
:
![]() =
=
 =
=
 =
=
 =
=
![]() =
=
![]() ;
;
2) Решение:
![]() =
=
![]() ;
;
Имеем
неопределенность вида
![]() .
Умножим числитель и знаменатель дроби
на выражение, сопряженное числителю,
то есть на
.
Умножим числитель и знаменатель дроби
на выражение, сопряженное числителю,
то есть на
![]() и найдем корни уравнения
и найдем корни уравнения
![]() :
:

![]() =
=
 =
=
=
 =
=
 =
=
=
 =
=
 =
=
=
![]() =
=
![]() =
=
![]() =
=
![]() ;
;
3) Решение:
![]() =
=
![]() ;
;
Имеем
неопределенность вида
![]() .
Преобразуем предел к виду второго
замечательного предела, то есть
.
Преобразуем предел к виду второго
замечательного предела, то есть
![]() :
:
![]() =
=
![]() =
=
![]() =
=
![]() =
=
=
![]() =
=
![]()
![]() =
=
![]() =
=
=
![]() =
=
![]() =
=
![]() .
.
Ответ:
1) 3, 2) -7, 3)
![]()
4. Найти указанные пределы, используя эквивалентные бесконечно малые функции.
1) ![]() ; 2)
; 2) 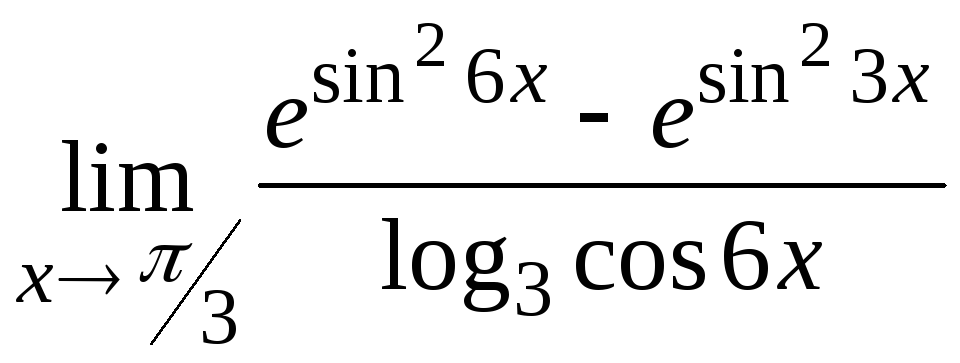 .
.
1) Решение:
![]() =
=
![]() ;
;
Имеем
неопределенность вида
![]() .
Преобразуем предел к виду первого
замечательного предела, то есть
.
Преобразуем предел к виду первого
замечательного предела, то есть
![]() :
:
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() .
.
2) Решение:
 ={
при
={
при
![]()
![]() ~
~![]() ,
,
![]() ~
~![]() .
В нашем случае при
.
В нашем случае при
![]()
![]() ,
,
![]() }=
}=
= =
=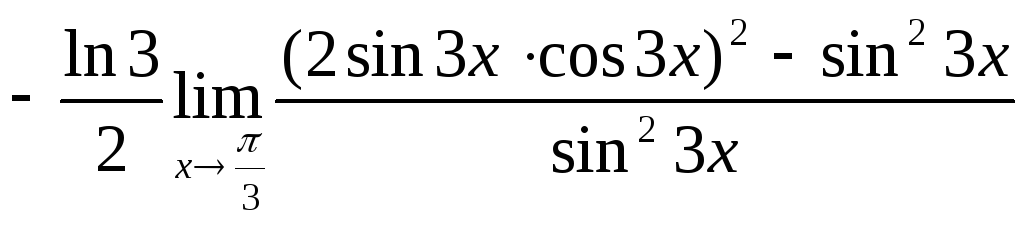 =
=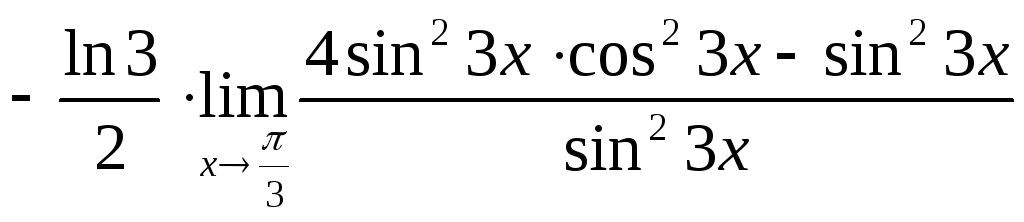 =
=
= =
=![]() =
=![]() =
=![]() =
=
=
=![]() =
=![]()
Ответ:
1)
![]() ,
2)
,
2)
![]()
![]()
5. Задана функция
![]() различными аналитическими выражениями
для различных интервалов изменения
аргумента. Найти точки разрыва функции,
если они существуют, и установить их
тип. Сделать чертёж.
различными аналитическими выражениями
для различных интервалов изменения
аргумента. Найти точки разрыва функции,
если они существуют, и установить их
тип. Сделать чертёж.
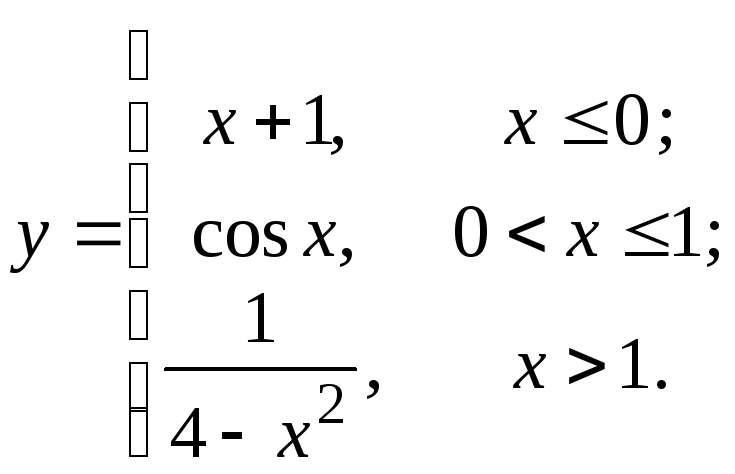
Поскольку
в точке
![]() функция не определена, то
функция не определена, то
![]() -
точка разрыва функции. Исследуем характер
разрыва. Найдем односторонние пределы
функции в точке
-
точка разрыва функции. Исследуем характер
разрыва. Найдем односторонние пределы
функции в точке
![]() .
.
![]()
![]()
Т.к.
оба предела равны
![]() ,
то
,
то
![]() -
точка второго рода
-
точка второго рода
Разрыв
возможен так же в точках
![]() и
и
![]() ,
в которых меняется аналитическое задание
функции.
,
в которых меняется аналитическое задание
функции.
Найдем
односторонние пределы функции в точке
![]() .
.
![]()
![]()
![]()
Т.к.
![]() (
(![]() )=
)=![]() (
(![]() )=
)=![]() (0)=1,
то в точке
(0)=1,
то в точке
![]() функция является непрерывной.
функция является непрерывной.
Рассмотрим
точку
![]() .
.
![]()
![]() (
(![]() )=
)=![]()
![]()
![]() (
(![]() )=
)=![]() =
=![]()
![]() (1)=
(1)=![]() =
=![]()
Односторонние
пределы конечны, но не равны между собой,
то
![]() -
точка разрыва первого рода.
-
точка разрыва первого рода.

