
Контрольная по ВМ №7, вариант 5
..doc345. Найти общее решение дифференциального уравнения первого порядка.
![]() .
.
Решение:
Приведём уравнение
к виду![]() .
.
![]() ;
;
![]() ;
;
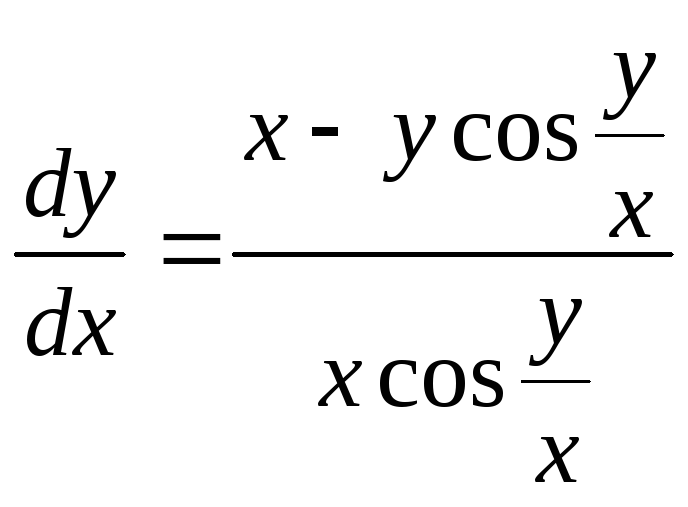 .
.
Проверим, является ли уравнение однородным.
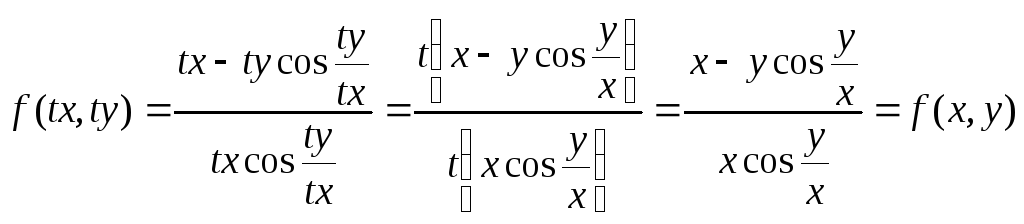 .
.
Уравнение является однородным, поэтому применяем подстановку
![]() ,
,
![]() ,
,
![]() .
.
Тогда:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ:
![]() .
.
355. Найти частное решение дифференциального уравнения, удовлетворяющее указанным
начальным условиям.
![]() ,
,
![]() ,
,
![]() .
.
Решение:
Рассмотрим соответствующее однородное линейное уравнение
![]() .
.
Его характеристическое уравнение
![]() ,
,
![]() ,
значит
,
значит
![]() ;
;
![]() .
.
Найдём частное
решение неоднородного уравнения
![]() .
.
![]() .
.
![]()
![]() ,
,
![]() .
.
![]() - не корень
характеристического уравнения.
- не корень
характеристического уравнения.
Тогда решение ищем в виде
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() -
не корень характеристического уравнения.
-
не корень характеристического уравнения.
Значит
![]() .
.
Частное решение будет в виде
![]()
![]() .
.
![]() ;
;
![]() .
.
![]() ;
;
![]() ;
;
![]() ,
,
![]() .
.
![]() .
.
Искомое частное решение:
![]() .
.
Общее решение неоднородного диф. ур-я:
![]() .
.
![]() .
.
Найдём частное решение, удовлетворяющее начальным условиям.
![]() .
.
![]()
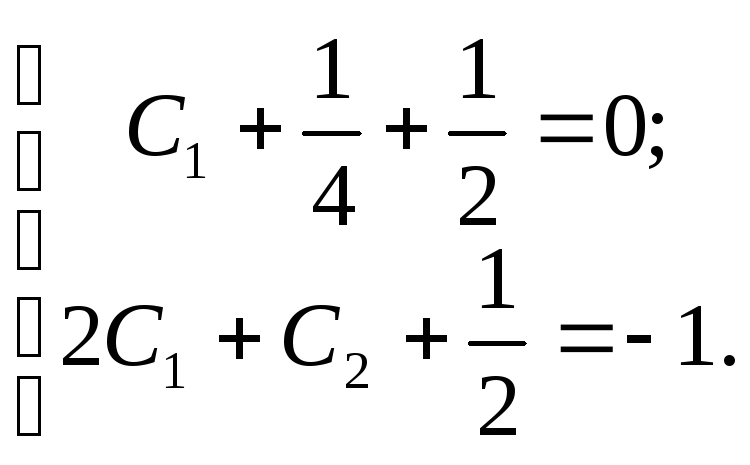
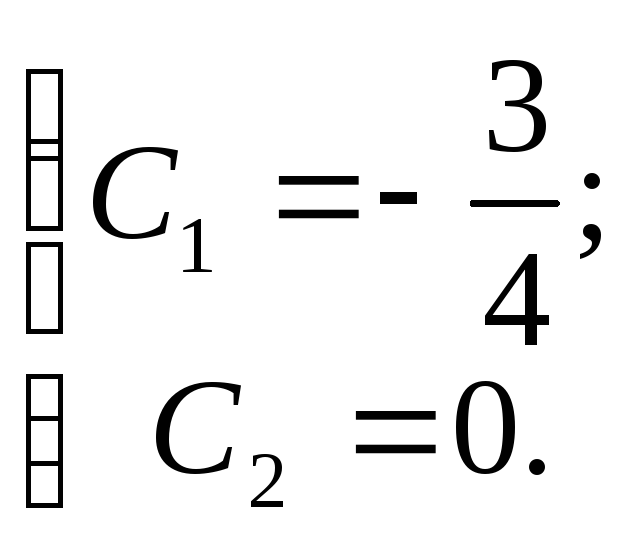
Ответ:
![]() .
.
365. Найти общее решение системы уравнений.
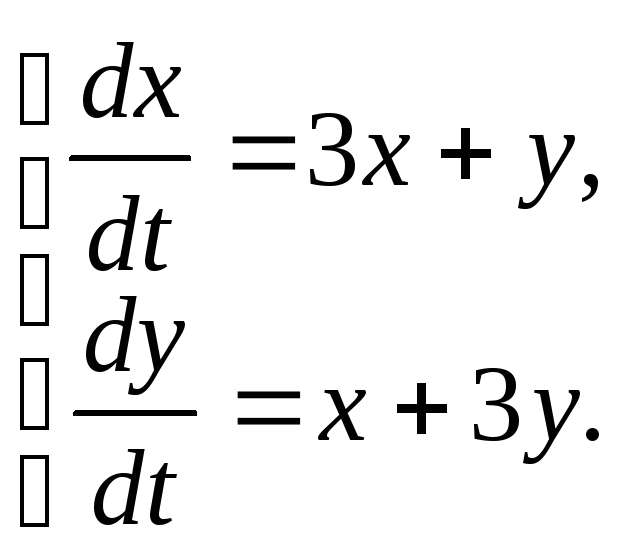
Решение:
Запишем систему в матричной форме:
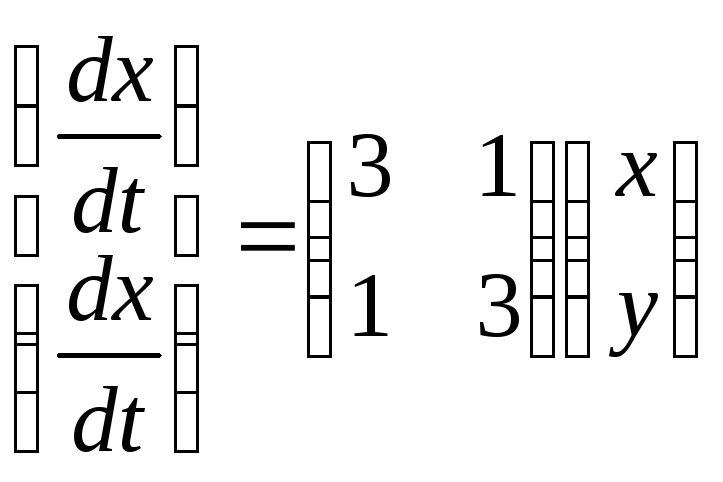 .
.
Составляем характеристическое уравнение матрицы системы:
![]() ,
,
![]() .
.
![]() .
.
Общее решение однородного уравнения имеет вид
![]() ;
;
![]() .
.
Найдём
![]()
![]() .
.
Ответ:
![]() ,
,
![]() .
.
375. По закону Ньютона скорость охлаждения тела в воздухе пропорциональна разности между
температурой тела и температурой воздуха. Если температура воздуха равна 200С и тело в
течение часа охлаждается от 100 до 300С, то через сколько минут (с момента начала
охлаждения) его температура понизится до 600С?
Решение:
Пусть Т - температура тела в момент времени t. За промежуток времени dt тело
охладится на dT градусов. Тогда скорость охлаждения характеризуется соотношением:
![]() .
.
По условию при dT=1ч.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
В момент времени
t=1
температура тела
![]()
![]() ;
;
![]() .
.
При
![]() ,
,
![]()
Ответ: 48мин.
