Контрольная по ВМ №9, вариант 5

445. Исследовать сходимость числового ряда .

Решение:

Сравним члены этого ряда с членами гармонического сходящегося ряда .

- сходящийся.

455. Найти интервал сходимости степенного ряда .

Решение:

Для вычисления радиуса сходимости применим формулу , где

. Получим 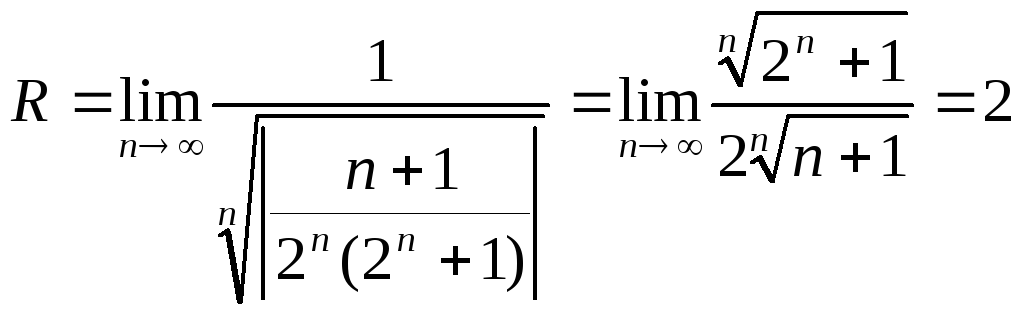. Значит, ряд

сходится на интервале (-2; 2). Исследуем сходимость ряда на концах интервала.

При получаем числовой ряд . Этот числовой ряд

расходится, т. к. .

При получаем числовой ряд , который тоже

расходится. Таким образом, исходный ряд сходится только внутри интервала

сходимости, т.е. при .

465. Вычислить определенный интеграл с точностью до 0,001. Для этого

подынтегральную функцию следует разложить в ряд, который затем почленно

проинтегрировать.

Решение:

Разложим подынтегральную функцию по формуле

.

Так как отрезок интегрирования [1; 0] находится внутри интервала сходимости

данного ряда, то ряд можно почленно интегрировать. Подставляя в интеграл

вышеприведенное разложение подынтегральной функции и почленно интегрируя в

указанных пределах, получаем

.

Ряд знакочередующийся. Погрешность замены суммы ряда суммой его первых n членов

по абсолютной величине меньше первого из отброшенных членов. И поскольку

, то для вычисления приближенного значения интеграла с требуемой

точностью достаточно взять первые три слагаемых.

Итак, .

475. Найти три первых отличных от нуля члена разложения в степенной ряд решения у=у(х)

дифференциального уравнения , удовлетворяющего начальному условию

у(0) = 1.

Решение:

Представим искомое решение в виде ряда Тейлора:

Здесь возьмем из начального условия, – из самого дифференциального

уравнения . Чтобы получить третье слагаемое ,

продифференцируем сначала обе части дифференциального уравнения, а затем

подставим туда .

.

Тогда решение имеет вид

.