
Контрольная № 3
.doc
Задача 84: ![]() .
.
Выделив в заданной функции полный квадрат, получить уравнение параболы и построить её график.
Решение:
Выделив полный квадрат в заданной функции, получим
![]()
Теперь применим метод преобразования координат. Известно, что график функции f(x)+b получают путём переноса графика f(x) вверх вдоль оси OY на b; график функции f(x-c) получается параллельным переносом графика f(x) при с < 0 в положительном направлении оси ОХ на с; а график функции y = - f(x) симметрично отобразится относительно оси OX. Тогда график исходной функции можно построить, переместив вершину параболы y = x² в точку O’(3;8) и затем отобразив параболу симметрично относительно оси OX.

Задача 94:  .
.
Задана
функция
![]() на
отрезке
на
отрезке
![]() .
Требуется: 1) построить график функции
в полярной системе координат по точкам,
давая аргументу
.
Требуется: 1) построить график функции
в полярной системе координат по точкам,
давая аргументу
![]() значения
через промежуток
значения
через промежуток
![]() ;
2) найти каноническое уравнение
полученной линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью, и по
уравнению определить тип линии.
;
2) найти каноническое уравнение
полученной линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью, и по
уравнению определить тип линии.
Решение:
1) построим график функции в полярной системе координат по точкам, давая значения через промежуток /8, начиная от =0;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3,24 |
6,83 |
26,27 |
─ |
26,27 |
6,83 |
3,24 |
2 |
1,45 |
1,17 |
1,04 |
1 |
1,04 |
1,17 |
1,45 |
2 |

2) найдём уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.
Из
условия
![]()
![]() ,
с другой стороны,
,
с другой стороны,
![]() ,
отсюда
,
отсюда
![]() ;
но
;
но
![]() ,
следовательно,
,
следовательно,
![]()
Искомое
уравнение – это уравнение параболы
![]() с вершиной в т.
с вершиной в т.
![]() .
График пересекает ось Х в т.
.
График пересекает ось Х в т.
![]() и
и
![]()
Координаты
т. С
![]() ,
т.
,
т.
![]() ,
т.
,
т.
![]()

Задача 104:1)  ;2)
;2)  ;
3)
;
3)  .
.
Найти указанные пределы, не пользуясь правилом Лопиталя.
Решение:
1)

2)
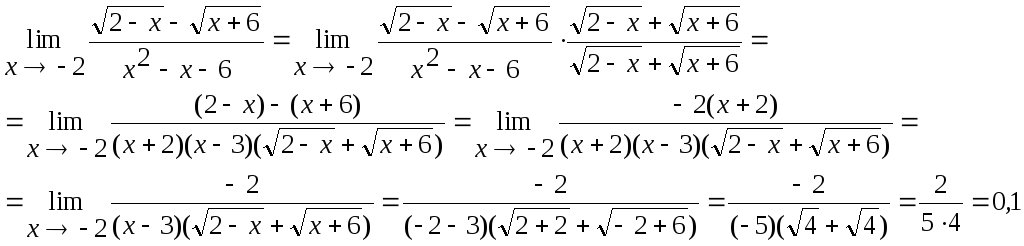
3)


Задача 114:1) ![]() ;2)
;2)  .
.
Найти указанные пределы, используя эквивалентные бесконечно малые функции.
Решение:
1)
![]() Полагая
Полагая
![]() .
Имеем
.
Имеем
![]()
2)
![]()
Задача 124:
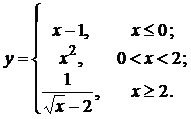
Задана
функция
![]() различными
аналитическими выражениями для различных
интервалов изменения аргумента. Найти
точки разрыва функции, если они существуют,
и установить их тип. Сделать чертёж.
различными
аналитическими выражениями для различных
интервалов изменения аргумента. Найти
точки разрыва функции, если они существуют,
и установить их тип. Сделать чертёж.
Решение:
Область
определения функции f(x)
– вся числовая ось
![]() .
Разрывы возможны только в точках
.
Разрывы возможны только в точках
![]() и
и
![]() ,
в которых изменяется аналитическое
задание функции.
,
в которых изменяется аналитическое
задание функции.
Найдем
односторонние пределы в т.
![]() и значение функции в этой точке:
и значение функции в этой точке:
![]()
![]()
Т.к.
в т.
![]() функции
функции
![]() определена,
конечные односторонние пределы существуют
и не равны между собой, то т.
определена,
конечные односторонние пределы существуют
и не равны между собой, то т.
![]() - точка разрыва первого рода.
- точка разрыва первого рода.
Найдём
односторонние пределы в т.
![]() и значение функции в этой точке:
и значение функции в этой точке:
![]()
![]()
Т.к.
в т.
![]() функции
функции
![]() определена, конечные односторонние
пределы существуют и не равны между
собой, то т. х=2 - точка разрыва первого
рода.
определена, конечные односторонние
пределы существуют и не равны между
собой, то т. х=2 - точка разрыва первого
рода.

